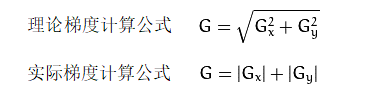在对图像的操作，我们采用模板对原图像进行卷积运算，从而达到我们想要的效果。而获取一幅图像的梯度就转化为：模板（Roberts、Prewitt、Sobel、Lapacian算子）对原图像进行卷积。

知识引入： 在一维连续数集上有函数f(x),我们可以通过求导获得该函数在任一点的斜率，根据导数的定义有： f ′ ( x ) = f ( x + Δ x ) − f ( x ) f'(x) = f(x+\Delta x) - f(x) f′(x)=f(x+Δx)−f(x) 在二维连续数集上有函数f(x,y),我们也可以通过求导获得该函数在x和y分量的偏导数，根据定义有： ∂ f ( x , y ) ∂ x f ( x + Δ x , y ) − f ( x , y ) \frac{\partial f(x,y)}{\partial x} f(x+\Delta x,y) - f(x,y) ∂x∂f(x,y)​f(x+Δx,y)−f(x,y)

∂ f ( x , y ) ∂ y f ( x , y + Δ y ) − f ( x , y ) \frac{\partial f(x,y)}{\partial y} f(x,y+\Delta y) - f(x,y) ∂y∂f(x,y)​f(x,y+Δy)−f(x,y)

对于图像来说，是一个二维的离散型数集，通过推广二维连续型求函数偏导的方法，来求得图像的偏导数，即在(x,y)处的最大变化率，也就是这里的梯度： g x = ∂ f ( x , y ) ∂ x f ( x + 1 , y ) − f ( x , y ) g_x = \frac{\partial f(x,y)}{\partial x} f(x+1,y) - f(x,y) gx​=∂x∂f(x,y)​f(x+1,y)−f(x,y)

g y = ∂ f ( x , y ) ∂ y f ( x , y + 1 ) − f ( x , y ) g_y = \frac{\partial f(x,y)}{\partial y} f(x,y+1) - f(x,y) gy​=∂y∂f(x,y)​f(x,y+1)−f(x,y) 梯度是一个矢量，则(x,y)处的梯度表示为： ∇ f ≡ g r a d ( f ) ≡ [ g x , g y ] T = [ ∂ f ∂ x , ∂ f ∂ y ] T ∇f \equiv grad(f) \equiv[g_x,g_y]^T = \begin{bmatrix} \frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \end{bmatrix}^T ∇f≡grad(f)≡[gx​,gy​]T=[∂x∂f​,∂y∂f​​]T

其大小为： M ( x , y ) = m a g ( ∇ f ) = g x 2 + g y 2 M(x,y) = mag(∇f)=\sqrt{g_x^2+g_y^2} M(x,y)=mag(∇f)=gx2​+gy2​ ​ 22大小的模板在概念上很简单， 但是他们对于用关于中心点对称的模板来计算边缘方向不是很有用， 其最小模板大小为33。3*3模板考虑了中心点对段数据的性质，并携带有关于边缘方向的更多信息。

Sobel算子是在Prewitt算子的基础上改进的，在中心系数上使用一个权值2，相比较Prewitt算子，Sobel模板能够较好的抑制（平滑）噪声。 为了工程化，减少计算量使用近似值计算公式，即实际梯度计算公式：

上述所有算子都是通过求一阶导数来计算梯度的，用于线的检测，在图像处理中，通常用于边缘检测。在图像处理过程中，除了检测线，有时候也需要检测特殊点，这就需要用二阶导数进行检测。

模板中心位置的数字是-8而不是-4，是因为要使这些系数之和为0，当遇到恒定湖对区域时，模板响应应将0。(如下图1) 用lapacian算子图像进行卷积运算时，当响应的绝对值超过指定阈值时，那么该点就是被检测出来的孤立点，具体输出如下： (如下图2)

DoG(Difference of Gaussian)算子和LoG(Laplacian of Gaussian)算子是常用的极值点检测(Blob Detection)两种方法，高斯卷积是为了进行尺度变换。

由于Laplace算子对噪声很敏感，所以一般利用高通滤波器进行平滑处理，所以引入了高斯拉普拉斯算子(LoG,Laplacian of Gaussian)

DoG即对不同尺度下的高斯函数的差分，DoG算子表达如下: D o G = Δ G σ 1 − Δ G σ 2 = 1 2 π [ 1 σ 1 exp ⁡ ( − ( x 2 + y 2 ) 2 σ 1 2 ) − 1 σ 2 exp ⁡ ( − ( x 2 + y 2 ) 2 σ 2 2 ) ] DoG = \Delta G_{\sigma 1}- \Delta G_{\sigma 2} = \frac{1}{\sqrt{2\pi}} \left [ \frac{1}{\sigma_1} \exp \left ( -\frac{(x^2+y^2)}{2\sigma_1^2} \right) - \frac{1}{\sigma_2} \exp \left ( -\frac{(x^2+y^2)}{2\sigma_2^2} \right) \right ] DoG=ΔGσ1​−ΔGσ2​=2π ​1​[σ1​1​exp(−2σ12​(x2+y2)​)−σ2​1​exp(−2σ22​(x2+y2)​)]

由于归一化的LoG算子： L n o r m = σ 2 [ G x x ( x , y , σ ) + G y y ( x , y , σ ) ] = σ ∂ G ∂ σ L_{\rm norm} = \sigma^2 \left [ G_{xx}(x,y,\sigma ) + G_{yy}(x,y,\sigma ) \right ] = \sigma\frac{\partial G}{\partial \sigma } Lnorm​=σ2[Gxx​(x,y,σ)+Gyy​(x,y,σ)]=σ∂σ∂G​

而： ∂ G ∂ σ ≈ G ( x , y , k σ ) − G ( x , y , σ ) k σ − σ \frac{\partial G}{\partial \sigma } \approx \frac{G(x,y,k\sigma)-G(x,y,\sigma)}{k\sigma-\sigma} ∂σ∂G​≈kσ−σG(x,y,kσ)−G(x,y,σ)​

所以： G ( x , y , k σ ) − G ( x , y , σ ) ≈ ( k − 1 ) σ 2 ∇ 2 G \bm {G(x,y,k\sigma)-G(x,y,\sigma) \approx (k-1)\sigma^2 \nabla^2G} G(x,y,kσ)−G(x,y,σ)≈(k−1)σ2∇2G

即DoG算子和LoG算子具有类似的波形，仅仅是幅度不同，不影响极值点的检测，而DoG算子的计算复杂度显然低于LoG，因此一般使用DoG代替LoG算子。