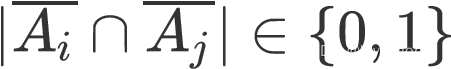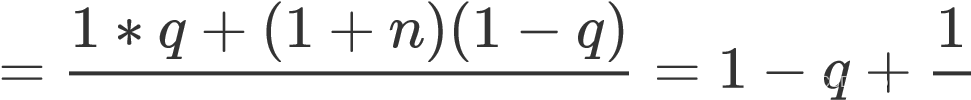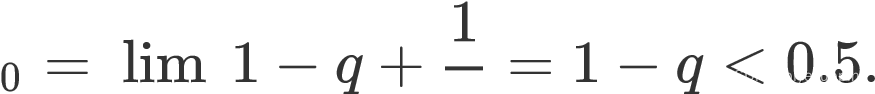基于C++实现的几何学与计算机的交叉应用（四色定理、三维凸包）

您所在的位置：网站首页 › 四色定理游戏怎么玩的好 › 基于C++实现的几何学与计算机的交叉应用（四色定理、三维凸包）

基于C++实现的几何学与计算机的交叉应用（四色定理、三维凸包）

2024-07-02 07:04| 来源: 网络整理| 查看: 265

浅谈几何学与计算机的交叉应用一、摘要

就计算机在几何学领域的应用,本文介绍了四色定理(Four Color Theorem)及其历史与机器证明,以及四色问题的求解.就几何学在计算机领域的应用,本文介绍了三维凸包(convex hull)表面积问题的求解.

关键词

四色问题;凸包

二、正文

国家的发展离不开日益密切的国际经济文化交流,学术也是一样.如今,学科交叉一词时常出现在我们眼前.

在进行数学科学的研究时,市场需要计算机辅助；在进行计算机科学的研究时,常常需要转化称数学问题

进行求解.如四色定理,开普勒猜想,NP-硬度的最小权重的三角测量,布尔毕达哥拉斯三元组问题等著名数学难题,均借助计算机得以证明；如凸包求解,时间复杂度(time complexity)计算,空间复杂度(space complexity)计算等问题.

几何学是数学的一大分支,本文将就四色定理和凸包求解问题,浅谈几何与计算机的交叉应用.

四色定理四色定理,又称四色猜想,是世界三大数学猜想之一.

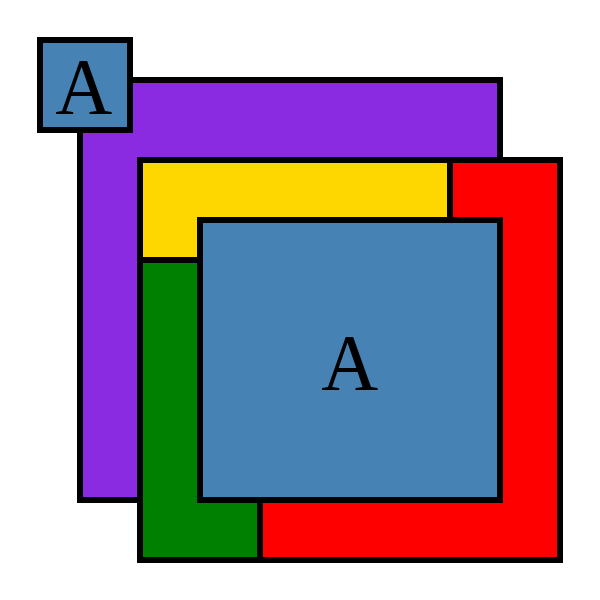
在这里插入图片描述

四色地图的一个例子

2.1 定理内容

如果在平面上划出一些邻接的有限区域,那么可以用四种颜色来给这些区域染色,使得每两个邻接区域染的颜色都不一样.

另一种通俗的阐述任意一个无外飞地(exclave)的地图都可以用四种颜色染色,使得没有两个相邻国家染的颜色相同.其中,外飞地为人文地理中的外飞地概念.若某国家 A 拥有一块与本国分离的领土 a , a 被其他国家包围, 则 a 称为 A 的外飞地.

在这里插入图片描述

外飞地的一个例子拓扑学阐述设有一平面或其一部分,将其划分为互不重叠的区域的集合.

定义地图:一个地图为以下方式的划分:

将平面划分为有限个区域,使得任意两个区域的交集是空集,所有的区域的并集是整个平面;所有区域中,只有一个区域是无界区域,其余区域都是有界区域.

其中,有界区域指能够用一个长和宽都有限的矩形覆盖的区域;无界区域则是指不能用这样的矩形覆盖的区域.每个区域相当于通俗说法中的国家.区域之间的边界相当于通俗说法中的国界线,定义为连续不自交的曲线,也称为连续简单曲线.

连续简单曲线是指一个连续函数: [0,1] → R2的像集= {c(t)∣t ∈ [0,1]},且满足= c(t2) ,0 t1 < t2 1,(t1 ,t2) = (0,1),

这样说明曲线不与自身相交.若 c(0) = c(1), 则称曲线为弧,否则称为圈.平面 R2 中的一个地图是指一个有限个连续简单曲线的集族

m= { Ci} ,m ∈ N ∩ [2,+∞).i=1 其中对 i = j ∈ N ∩ [1,m],Ci = {ci( t)∣t ∈ [0,1]}是连续函数ci : [0,1] → R2的像集,且满足ci( t1) = ci( t2) ,0 t1 < t2 1,(t1, t2) = (0,1),且∣Ci ∩ Cj∣ ∈ {0,1}.

定义边: L 中每一个连续简单曲线.

定义顶点:任意边 C 的端点 c(0),c(1) 称顶点.

定义中性点: 所有属于边或顶点的点.其集合NL = {x∣x ∈ Ci,i ∈ N ∩ [1,m]}.

定义国家: L 将非中性点划分成的若干个道路连通的开集.其集族 AL.

可见,每个国家是 R2 NL 的一个极大连通子集,是没有外飞地的;取一个非中性点 x, 所有能够从 x 经过一条不含中性点的弧到达的点构成的集合,就是一个国家.定义 n-染色:地图 L 的一个 n-染色方案指一个函数: AL → N ∩ [1,n].若Ai) = f(Aj) ,Ai, Aj ∈ AL,

在这里插入图片描述

则称它是可行的.四色定理:每个地图都存在可行的 4-染色方案,即L,f : AL → {1,2,3,4},s.t.,f(Ai ) = f(Aj) ,Ai, Aj ∈ AL ,

在这里插入图片描述

图论阐述

将上述地图转化为图论中的一个无向平面图,即地图中的每一个国家用其内部的一个点代表,作为一个顶点.如果两个国家相邻,就在两个顶点之间连一条线.

在这里插入图片描述

地图与无向平面图互相转化的一个例子

四色定理:必然可以用四种颜色给无向平面图的顶点染色,使得相连的顶点颜色不同.

2.2 历史

年,古德里(Francis Guthrie)提出猜想:“只需要四种颜色为地图着色”.年,肯普(Alfred Kempe)宣称证明了四色定理.11 年后,肯普的证明被希伍德(P. J. Heawood)推翻.他举出了反例,并提出了五色定理.但近代,该反例又被董德周推翻.

伯克霍夫(George David Birkhoff)证明了由不超过 12 个国家构成的地图都能用四色染色.9 年后, 他的学生富兰克林(Philip Franklin)证明了由不超过 25 个国家构成的地图都能用四色染色,阿佩尔(K. Appe)和哈肯(W. Haken)使用计算机辅助证明了四色定理 ,但是他们的证明在当时并未获得普遍认可.主要原因为使用计算机的部分无法用手算核实,应该用手算核实的部分因过于繁琐,无人能够独立完成.,西缪尔(P. Seymour)等人对阿佩尔和哈肯的证明进行了修正和改进,同时证明了其正确性.龚提尔(Georges Gonthier)使用证明验证程序 Coq 来对当时交由计算机运算的算法程序进行了形式上的可靠性验证.验证表明,四色定理的机器验证程序确实有效地验证所有构形的可约性,完成了证明中的要求.

2.3 计算机辅助证明 2.3.1 可约构形

考虑 n + 1 个国家中邻国数目最小的国家 A , A 的邻国的数目不超过 5. 若 A 的邻国数目不超过 3, 那么可以把 A 去掉(如和其中一个邻国连成一体),形成一个 n 个国家的地图,这个地图可以用四种颜色着色, 而原来的 3 个邻国至多用了三种颜色.这时候将 A 还原,染上第四种颜色,就等于找到给用四种颜色原地图着色的方法.

这种能够去掉一个国家,减少国家数的局部称可约构形(reducible configuration).

2.3.2 不可避免的可约构形集

伯克霍夫等人的证明是肯普的方法的延续和系统化,归纳为寻找一个不可避免的可约构形集(an unavoidable set of reducible configurations,简称不可避免集). 在这里插入图片描述

肯普使用的不可避免集

2.3.3 放电法

将无向平面图其看作是平面的电网,并将每个点按照度数(degree,连出的边数)分类.首先在每个度数为 k 的节点放置 6 k 的电荷.

放电过程(discharging procedure)指将这些电荷以特殊的规则进行重新分配,从而找出电网结构上的特性,创建不可避免集.具体来说,可以假设某些构形全不存在,然后构造一个放电过程,使得接受电荷的总量不再等于释放电荷的总量,从而导出矛盾.每个良好设计的放电过程都能证明一个不可避免集的存在. 阿佩尔和哈肯的证明二人通过纸笔运算,得到了一个由 1936 个构形构成的不可避免集,对应的放电规则由 487 条规则构成.经过电脑 1200h 的验证,得出这 1936 个构形均为可约构形,四色定理得证.

2.3.4 西缪尔等人的证明

经过修正和改进,不可避免集大小减至 633 ,放电法则减至 20 个,图着色算法由 4 次时间算法优化为 2 次时间算法,证明所需机时由 1200h 缩短到 24h .此外,第二代证明达到了人工复核的要求,如果用计算机验证只需 5min 就能完成,且没有第一代证明中只有计算机才能完成的验证过程.

2.3.5 机器证明的可靠性问题

龚提尔(Georges Gonthier)使用证明验证程序 Coq 来对当时交由计算机运算的算法程序进行了形式上的可靠性验证.证明验证程序是一个由法国开发的软件,能够从逻辑上验证一段电脑程序是否正常运行,并且是否达到了它应该达到的逻辑目的.验证表明,四色定理的机器验证程序确实有效地验证所有构形的可约性,完成了证明中的要求.至此,四色定理的理论部分和计算机证明算法部分都得到了验证.

2.4 四色问题

称求得一个给定的无外飞地的地图的一种可行的 4-染色方案的问题为四色问题.

四色定理已证,意味着四色问题总是有解的,在求解四色问题时,不需要考虑答案存在性问题.

下面给出一种使用计算机求解四色问题的方法.

输入输入数据为一张对比度较高的图片. 在这里插入图片描述

输入数据的一个例子

将输入空地图转化为 bool 型矩阵储存,矩阵内每一个变量数值与像素点的颜色有关.

国家处理使用深度优先搜索(BFS)标记国家.该标记过程可视为将每个国家染上不同颜色.

在这里插入图片描述

上例国家处理后

2.4.1 邻国处理

若来自不同国家的两个像素(矩阵内变量)足够近,那么认为这两个国家是邻国.

已知每个国家必然有邻国;每条边的可视为多个矩形相连;同时不可能出现违反四色定理的地图.通过上述

规则的约束,通过二分法确定认为足够近的距离数值.

在这里插入图片描述

上例邻国处理后(绿点为两个国家最近的像素处)

2.4.2 颜色填充

填充颜色有多种算法,这里使用威尔士-鲍威尔算法(Welsh-Powell Algorithm,下文简称 WP)和基于广度优先搜索(DFS)的回溯填色算法(下文简称 D)两种即可.

定义最优解:四色问题的一个最优解是一个存在可行的 n-染色方案但不存在可行的(n-1)-染色方案的地图的一个可行的 n-染色方案.

定义简单图:可用 WP 求解四色问题的地图.大部分地图都是简单图.

WP较快,但是在面对非简单图时不能成功填色;同时,面对一些存在可行的n-染色方案( 1 n 3 )的地图时,仍然需要四种颜色,即所得解不是最优解.

D 较慢,但是适用于任何地图,且得到的是最优解.

填色时,可以选择两种方案:

方案一:先使用 WP,若失败,则再使用 D.

方案二:直接使用 D.O(D)WP 和 D 的时间复杂度 O(WP),O(D) 差异是以数量级体现的,设 n = , n 与地图的复杂程度正相关.再假设简单图占比为 q > 50%.利用假设的数据,通过计算,发现方案一二的时间复杂度之比为

在这里插入图片描述

当地图趋于复杂时

在这里插入图片描述

故选择方案一较快.

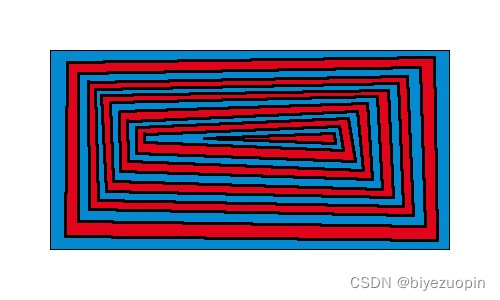
在这里插入图片描述

上例染色完成

Loading pixels... Analyzing areas & finding nodes... Found a total of 12 areas/nodes. Analyzing marginal points & finding edges... Found marginal points for all areas. Found a total of 11 edges. Building & solving graph, stand by... Calculating valence... Node 1 has highest valence: 2 Coloring successful with Welsh-Powell algorithm! Finished.

上例求解时所得中间结果日志

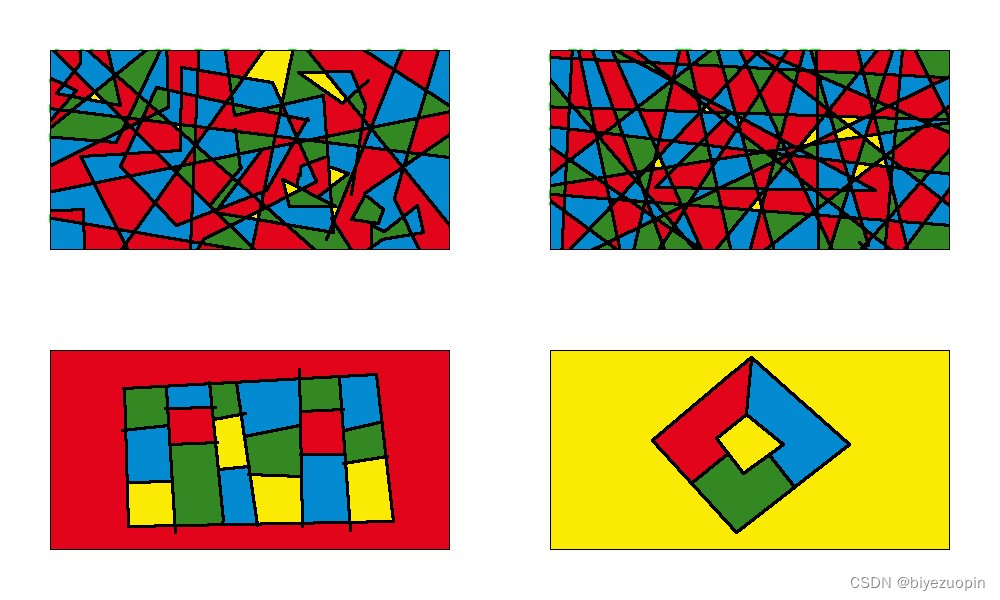
在这里插入图片描述

拓扑同构的图形在 WP 下均未得到最优解且颜色数目不同

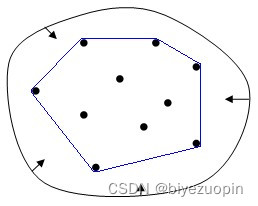
在这里插入图片描述

其它地图染色完成示例

2.5 三维凸包

在点集拓扑学与 RJ 中,凸集(convex set)是一个点集合,其中每两点之间的直线点都落在该点集合中.

在一个实数向量空间 V 中,对于给定集合 X ,所有包含 X 的凸集的交集 S = K 被称为 X 的XKV凸包.

可以用 X 内所有点 (x1, x2, ,xn) 的线性组合来构造 X 的凸包

= {∑tjx j∣ xj ∈ X,∑ tj = 1,tj ∈ [0,1]}.

在 R2 中,凸包可想象为一条刚好包着所有点的橡皮圈.

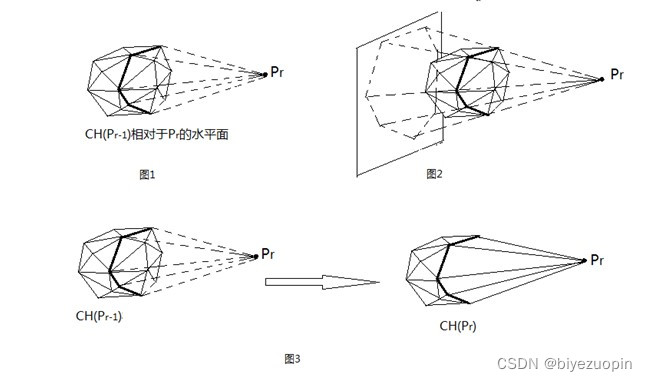
在这里插入图片描述

蓝色即为这 10 个点所得凸包

2.5.1 联系

在算法竞赛中,经常要编程求二维凸包,偶尔会出现三维凸包.

数学上求凸包时,可用增量法,Jarvis 步进法,Graham 扫描法,单调链法,分治法,Akl-Toussaint 启发式快包法.

算法竞赛中求凸包时,常用增量法,Jarvis 步进法,Graham 扫描法.

而这里给出增量法求 R3 中一些点的三维凸包的表面积过程.

2.5.2 算法设计

初始,先选三个不共线的点,组成一个面.其实应该是正反两面的,即将正反两面均加入凸包的面集.逐次将点加入,然后检查之前的点是否在新凸包上.

当加入点 Pr 时,想象从该点看向旧凸包 CH(Pr1) ,删除 CH(Pr1) 中 Pr 可以看到的面,然后将所有Pr 能看到的点与 Pr 连线,其中连续两点和 Pr 构成三角形,得到新凸包 CH(Pr) .

在这里插入图片描述

加入点同时更新凸包的过程

由于每次都要检查所有之前的点,时间复杂度为 O(n2). 为进一步优化算法,笔者在误差允许范围内将各点的位置震荡,以达到使所得凸包的各面均为三角形的目的.

在求三维凸包的过程中,出现了两种向量:一种是由一个点指向另一个点的向量,另一种是由两个已知求叉积所得向量. 其中,第一种向量需要额外记录其始终两点.虽然终点和可由其始点和向量方向和长度计算得来,但算法竞赛中通常牺牲空间来节省时间,故均需开辟空间记录.

得到两个向量类：

class Vector1 { public: double x,y,z; double l; double len() { return (l=sqrt(x*x+y*y+z*z)); } double lx,ly,lz,rx,ry,rz; }; class Vector2 { public: double x,y,z; double l; double len() { return (l=sqrt(x*x+y*y+z*z)); } };

其中 len() 函数的作用是计算向量长度. 由于算法设计,笔者将这两类向量以及给出的点均用同一个类 P 存储：

class P { public: double x,y,z; void ck() { x+=rv; y+=rv; z+=rv; } void pin() { scanf("%lf%lf%lf",&x,&y,&z); ck(); } void ot() { printf("%.5lf %.5lf %.5lf\n",x,y,z); } double len() { return sqrt(x*x+y*y+z*z); } P operator+(P r) { return (P) { x+r.x,y+r.y,z+r.z }; } operator-(P r) { return (P) { x-r.x,y-r.y,z-r.z }; } operator/(P r) { return (P) { y*r.z-z*r.y,z*r.x-x*r.z,x*r.y-y*r.x }; } double operator*(P r) { return x*r.x+y*r.y+z*r.z; } };

其中, ck() 为震荡函数,重载 + 和重载 - 为向量加和向量减,重载 / 为叉积,重载 * 为点积.

而对凸包的面,笔者用类 S 存储：

class S { public: int v[3]; void ot() { printf("%d %d %d\n",v[0],v[1],v[2]); } P sp() { return (p[v[1]]-p[v[0]])/(p[v[2]]-p[v[0]]); } double sa() { return sp().len()/2.0; } int ck(P pp) { return ((pp-p[v[0]])*sp()>0); } };

我们知道,三角形面积等于其任意两边的叉积长度的一半,即其中函数 sa() . 计算凸包所有面的面积之和,即为其表面积. 设该凸包面集大小为 F ,由于该凸包所有面均为三角形,那么其边集大小 E =

在这里插入图片描述

由欧拉公式

2.5.2 + V E = 2

得,其顶点集大小

= 2 + E F =

在这里插入图片描述

【本文地址】

基于C++实现的几何学与计算机的交叉应用（四色定理、三维凸包）

基于C++实现的几何学与计算机的交叉应用（四色定理、三维凸包）

今日新闻

推荐新闻