线性代数在计算机图形学中的应用

您所在的位置：网站首页 › 向量的叉乘积怎么算 › 线性代数在计算机图形学中的应用

线性代数在计算机图形学中的应用

#线性代数在计算机图形学中的应用| 来源: 网络整理| 查看: 265

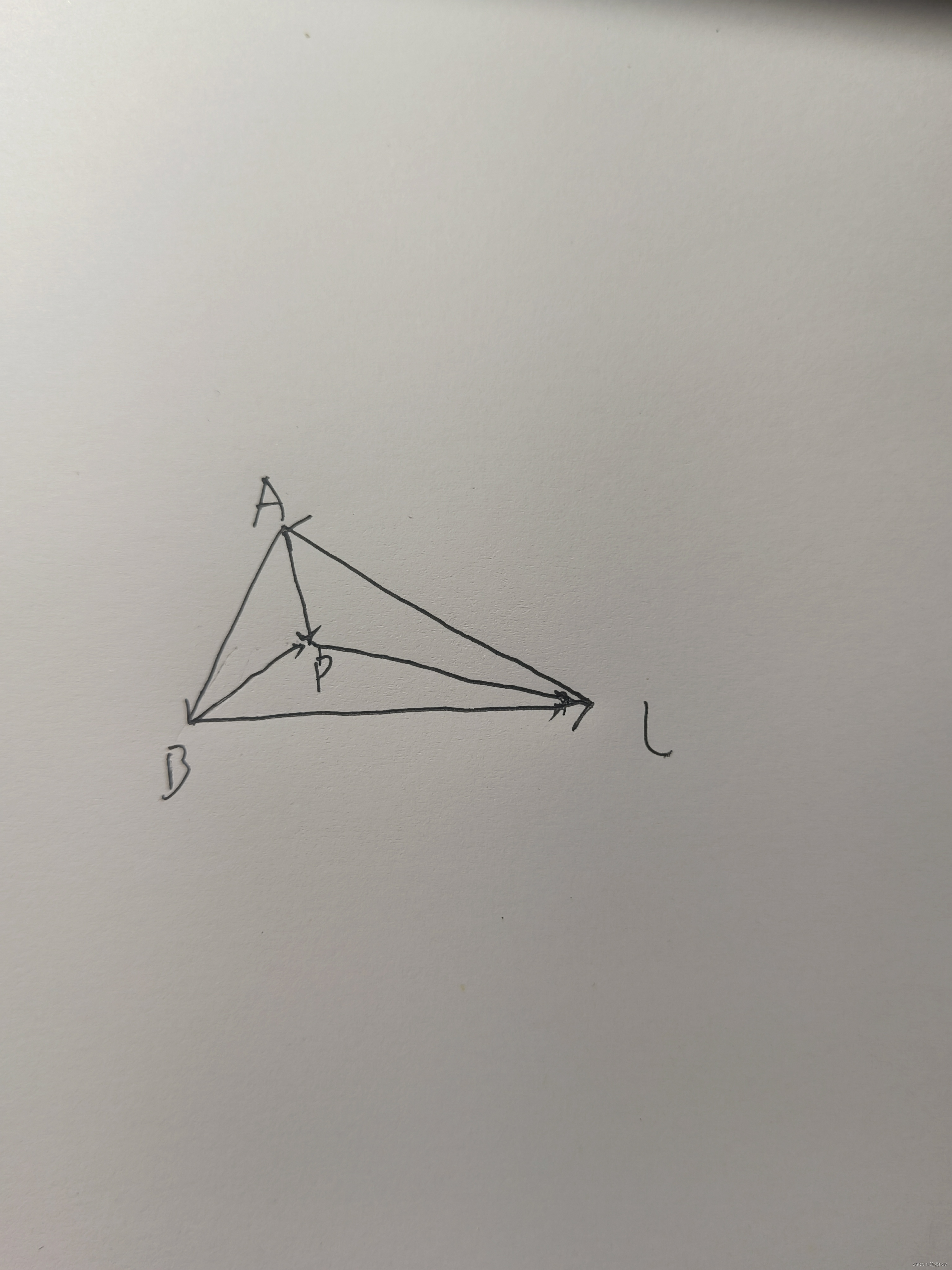
文章背景：本学期我学习了计算机图形学，我发现背后都是由线性代数的知识作为支撑的，于是我想把目前我了解到的一些数学知识总结出来。另外，本文在举例时主要采用计算机游戏的场景来进行举例，以更好地说明这些数学概念或公式的应用。

（本文章为课程作业）

线性代数是计算机图形学中的基础数学理论之一，广泛应用于3D图形的建模、变换和渲染等方面。本文将介绍线性代数在计算机图形学中的常见应用以及个人的一些理解。

一.向量的基本运算 1.向量的点积

对于一些3维的游戏来说，游戏场景中的每一个点都可以看作是三维笛卡尔坐标系中的一个坐标点，记为 $(x,y,z)$ ，我们假设规定游戏场景中的一点为坐标原点，那么其他的点的坐标皆可以表示为一个三维的空间向量。

$\mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2 + a_3 b_3 = |\mathbf{a}| |\mathbf{b}| \cos\theta$ 是三维空间中的点积表达式，我们可以看到点积是和两个向量之间的夹角相关的，那么根据两个向量的夹角就可以做出判定，比如说我们假设一个射击游戏的场景，一把散弹枪的射击范围是一个扇形，那么我们可以选取这把枪射击范围内的两个点，与枪的位置形成了两个向量，对这两个向量做点积，并求出其夹角，如果算出来的角度比枪械预先设置的角度还要大，那么我们就有可能判定这个玩家开挂了，他可能开了增范围的挂。

我们还可以根据两个向量的点积来判断两个点之间的位置关系，如果这两个点和同一个点所连向量的点积越接近1，同时夹角越接近0，那么我们就可以得出这两个向量越接近，也就是终点越接近，也就是这两个点越接近，我们可以根据预先设定的一些参数，来判定这两个点的接近程度，应用到游戏场景里，可以理解为碰撞体积，也就是到达一定范围内就会视为碰撞。

2.向量的叉积

对于叉积我们知道有 $\mathbf{a} \times \mathbf{b} = -\mathbf{b} \times \mathbf{a}$ ，也就是说对于叉积来说，交换顺序后要添一个负号，两个向量交换后（或许可以理解为它们的终点进行了交换），产生的第三个向量的是方向相反的向量，那么我们可以根据产生向量的方向来判定两个向量的左右关系。

我们还可以根据叉积来判断一个点在不在一个三角形内部，如下图所示。

三角形的方向是逆时针的，从向量AB叉到向量AP叉出来的方向是+ z（这里我们规定垂直于直面向外的方向为+z，垂直于纸面向里的方向为-z）,说明P点在AB的左侧（这里我们规定得到+z方向的为左侧，否则为右侧）；从向量BC叉到向量BP叉出来的方向是+ z,说明P点在BC的左侧;从向量CA叉到向量CP叉出来的方向是+ z,说明P点在AC的左侧,这就说明P点在三角形的内部。因为如果不在的话那么至少存在一条边使得P点在右侧。这一原理使得我们可以在一个场景中判断一个人物在不在规定的范围内，当然游戏中的场景一般不可能只是三角形，但是我们根据这一原理，可以把判定方法推广到多边形中。

3.向量的混合积

在有些游戏场景中，我们需要判断一个人物先后的两次位置是否在规定的同一平面内，我们可以找这个平面内的任意不平行于这两个点所连向量（记为向量 $\mathbf{a}$ ）且线性无关的向量，并对它们做叉积，得到的结果再与 $\mathbf{a}$ 进行点积，如果结果为0，那么说明该人物在规定平面内，上述计算过程其实就是混合积的计算。

二.矩阵变换

线性变换可以看作是一个矩阵与原来的向量相乘，因此矩阵变换是通过矩阵与向量相乘的方式实现的。在计算机图形学中，常见的矩阵变换包括平移、旋转和缩放等。

1.缩放

缩放变换可以通过如下的矩阵来实现。

$\begin{bmatrix}x^{'}\\y^{'}\\z^{'} \end{bmatrix}=\begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & s_z \\ \end{bmatrix}\begin{bmatrix}x\\y\\z \end{bmatrix}$

实现缩放变换的矩阵是一个对角矩阵，其中元素 $s_x,s_y,s_z$ 分别表示在x轴、y轴和z轴上的变换比例，当缩放比例为负数时，会出现镜像效果，也就是物体会在相应方向上进行翻转。

2.旋转

二维旋转矩阵的表达式为：

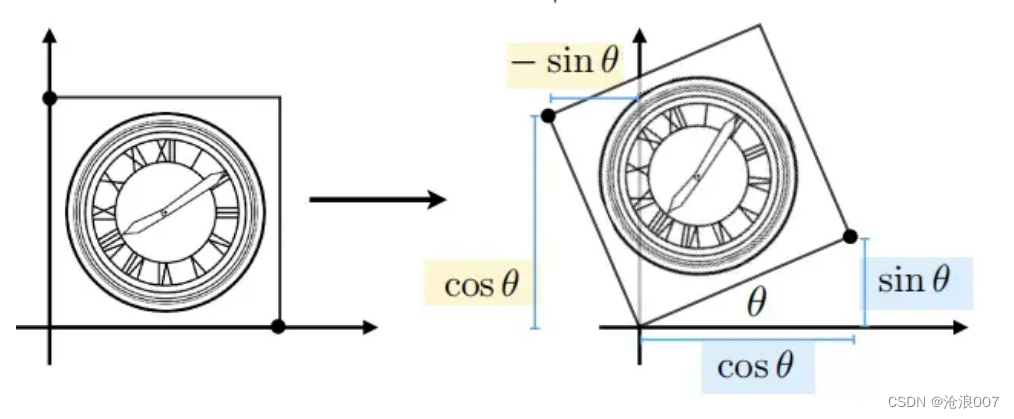
$\begin{bmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \ \end{bmatrix}$

其中， $\theta$ 表示旋转角度，实现的效果如下图所示。

这个矩阵描述了绕原点逆时针旋转角度为 $\theta$ 的变换。其中， $\cos\theta$ 表示旋转角度的余弦值， $\sin\theta$ 表示旋转角度的正弦值。通过对一个向量应用该矩阵，可以实现相对于原点的旋转变换。

游戏场景中经常会有旋转的场面，但是需要特别注意的是该旋转矩阵是针对原点进行，如果需要围绕不是原点的旋转中心进行旋转，需要先进行平移变换，将旋转中心移动到原点，然后再进行旋转，最后再逆向平移回原来的位置。

如果我们把旋转变化扩展到三维，同样可以用一个矩阵来表示旋转变换，下面我们以绕三个坐标轴旋转为例绕 x 轴旋转的矩阵（绕 x 轴的俯仰角）： $R_x(\phi) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\phi & -\sin\phi\\ 0 & \sin\phi & \cos\phi\ \end{bmatrix}$ 绕 y 轴旋转的矩阵（绕 y 轴的偏航角）： $R_y(\theta) = \begin{bmatrix} \cos\theta & 0 & \sin\theta\\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \\ \end{bmatrix}$ 绕 z 轴旋转的矩阵（绕 z 轴的滚转角）： $R_z(\psi) = \begin{bmatrix} \cos\psi & -\sin\psi & 0 \\ \sin\psi & \cos\psi & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}$ 其实我们可以观察到绕三个轴旋转的矩阵其实就是在二维矩阵上进行了一些变动，添加了一行一列，而其中只有在对角线的元素为1

三维旋转矩阵可以通过按顺序相乘这些矩阵来表示组合旋转。例如，按顺序先绕 z 轴旋转，然后绕 y 轴旋转，最后绕 x 轴旋转的组合旋转矩阵为： $R = R_x(\phi) \cdot R_y(\theta) \cdot R_z(\psi)$ 这样，对一个向量应用矩阵 R，可以实现相对于原点的复合旋转变换。

3.平移

矩阵的平移公式可以使用齐次坐标来表示。齐次坐标是一种用于表示三维空间中点和向量的坐标系统，它引入了一个额外的分量来表示平移。对于三维平移变换，平移矩阵的表达式如下： $T = \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$ 其中， $t_x$ 、 $t_y$ 和 $t_z$ 分别表示在 x、y 和 z 轴方向上的平移量。这个矩阵是一个 4x4 的矩阵，但是这并不代表这是面对4维的情况，事实上，这是由于引入了一个新的分量。除了对角线上的元素为 1 外，第四列表示平移向量。通过对一个点或向量应用平移矩阵，可以将它沿各个轴方向平移指定的距离。需要注意的是，在使用齐次坐标表示的情况下，点的表示是通过除以最后一个分量来获取其三维坐标，而向量的表示则应该忽略最后一个分量。

4.矩阵的一些运算法则在计算机图形学中的理解

对于矩阵来说，一般是不满足交换律的，也就是说AB一般是不等于BA的，把这个对应到计算机图形学中很容易理解，比如说对一个图像进行处理，先旋转后缩放和先缩放后旋转得到的图像一般是不一样的。

对于矩阵求逆的运算，我们也可以有对应的理解，假设我们对一个图像（假设这个图为矢量图）先做变换一（其对应的矩阵为矩阵A），再对这个图像做变换二（对应的矩阵为B），等于对于该矢量图中的每一个向量左乘矩阵 $BA$ ，得到了新的图像，那么我们要将新的图像恢复为原来的图像，就应该先做变换二的逆变换，再做变换一的逆变换，这样等价于对新图像左乘矩 $A^{-1}B^{-1}$

那么上面的过程，其实就对应了矩阵求逆的过程 $\left ( BA \right )^{-1}=A^{-1}B^{-1}$

三.三维场景向二维图像的变换

我们都知道在计算机图形学中很多场景都是立体的，但是由于计算机屏幕或者说其他屏幕看到是平面的，它们展示的也肯定是二维的图像，那么我们就需要有把三维的场景转换成二维图像的工作。

1.模型变换

对于一个三维的物件，我们需要把它摆放到我们想要的位置，同时物体的朝向等都要调整，这里就需要用到上文矩阵变换的知识了，我们进行一系列平移、旋转、缩放的操作就可以实现模型转换的目的。

2.视角变换

我们可以想象一下摄像机本身就有一个自己的坐标系，那么怎么计算出摄像机和物体的相对位置呢？我们可以基于这样的一个假设：如果摄像机和所有的物体一起移动的话，那么我们拍出的照片效果是一样的。

那么我们就需要把摄像机的坐标系变换为和物体一样的坐标系，我们需要两步操作，第一步是把摄像机移到物体坐标系中的坐标原点，第二步是把摄像机的坐标系 $\left ( x_1,y_1,z_1 \right )$ 旋转为物体的坐标系 $\left ( x,y,z \right )$ ,变换矩阵如下，其中右边的矩阵实现了移动的操作，而左边的矩阵实现了旋转（或者说坐标变换）的操作。

$M = \begin{bmatrix} x_u & y_u & z_u & 0 \\ x_v & y_v & z_v & 0 \\ x_w & y_w & z_w& 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$

3.投影变换

经过上述的操作后，场景仍然是三维的，我们想要把它们变成二维的，就需要进行投影变换，把三维场景投影到二维，包括正交投影，透视投影等方法。当然真实的计算机图形学中，这一过程非常复杂，进行投影后，还需要进行视口变换，光栅化等一些列过程，但是它们仍然是以矩阵和线性代数为基础内容。

以上就是我在学习计算机图形学中总结的一些和线性代数有关的知识。

【本文地址】

线性代数在计算机图形学中的应用

线性代数在计算机图形学中的应用

今日新闻

推荐新闻