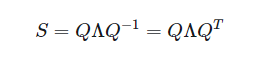《本科 |
您所在的位置:网站首页 › 双线性函数满秩的充要条件 › 《本科 |
《本科
|
我的线代笔记 基础知识 逆矩阵总结 矩阵的秩 单射、满射、双射 线性相关与线性无关 矩阵函数的四个重要概念 矩阵的秩和线性方程组的解 转置矩阵的性质 列空间、行空间、零空间之间的关系 行列式 相似矩阵和二次型 等价矩阵的定义 相似矩阵 相似矩阵的定义 相似矩阵的性质 相似矩阵的用途 矩阵对角化 对角化的定义 对角化的条件 特征向量和特征值 特征值的相关性质 特征空间的定义 正交阵的定义 施密特正交化得到标准正交基 对称矩阵 对称矩阵的定义和性质 对称矩阵的对角正交化 二次型矩阵的性质 矩阵合同 标准型与规范型 二次型的标准型化法 正定矩阵 向量空间补充 矩阵A(m,n)作用下的向量映射 空间映射 矮胖矩阵: 高瘦矩阵: 方块矩阵: 零空间: 列空间: 向量空间及其子空间 定义 矩阵A(m,n)的四个重要的子空间 行、列、零、左零四个重要空间的关联性 空间之间的关系 最小二乘法求近似解 简化投影计算的方法 特征值(EVD)分解降维 基础知识 线性函数需满足可加性、齐次性。向量空间的维度 = 向量空间的基的个数 = 向量组的秩 零向量空间是没有基的,零向量与任意向量正交,且与任意向量线性相关!AB均是向量空间V的基,则AB是等价向量组,他们的张成空降相同,span(A)=span(B)当AB向量正交时,AB相互独立使用余弦距离解释向量之间的关系:两根向量夹角越小,关系越紧密,两根向量垂直,彼此之间就没有关系,相互独立如果以向量空间作为自变量,这样的函数就称为向量函数有一种特殊的向量函数,其自变量是向量空间,因变量也是向量空间,这样的函数称为“矩阵函数”,通常用A表示,也就是矩阵。初等行变换:在单位矩阵的行上进行倍加、倍乘、对换。在单位阵上应用这三种初等行变换一次得到的矩阵称为初等行矩阵。初等行矩阵乘上矩阵A,就相当于在矩阵A上实施了对应的初等行变换。同型矩阵可以相加,对应位置元素相加即可,跟向量加法运算规则一样。对称矩阵:A的转置等于A,对称矩阵一定是方阵。反对称矩阵:A的转置等于-A,反对称矩阵一定是方阵。矩阵A左乘x,Ax可以将x逆时针旋转θ角 逆矩阵总结 只有方阵才能是满秩矩阵,满秩矩阵存在逆矩阵。也就是 |A|≠0矮胖矩阵A(m,n),mn不存在逆矩阵,因为在目标空间中的某个y可能找不到原始空间的某个x与之对应。比如A(3,2)映射后的目标空间是R^3,但是实际上映射的结果是R^3中的一个二维平面。在平面外的目标空间中的任意一点找不到原始空间的x与之对应。 矩阵的秩 列秩:即A的列空间的维度,也就是列向量组的秩,记做rank(col(A)),矩阵的列向量组线性无关则称为列满秩,单射。反之,列向量组线性相关则列不满秩,非单射,非单射则Ax=0有非零解。不会升维:值域的维度小于等于定义域的维度,也就是不会出现升维的情况。行秩:行向量组的秩叫做行秩,行向量组线性无关,称为行满秩。行秩=列秩。由m个行向量组成的向量组的秩为m,则行向量组满秩,即行满秩。 单射、满射、双射 单射:每一个y至多有一个x与之对应,对于矩阵函数Ax=y,如果定义域和值域维度相同则为单射。如果变换后值域维度缩小则不是单射。单射等价于列满秩满射:每一个y至少有一个x与之对应。此时值域与到达域相等。 对于线性函数而言,满射只可能全部是一对一或全部是多对一,不会两者同时在一个映射中存在。满射等价于行满秩。 矩阵A行满秩,则Ax=b为满射,则方程存在解且不唯一。 双射:既是单射又是满射,称为双射,也就是一一映射。双射等价于行满秩+列满秩。既是列满秩又是行满秩(行秩=列秩)的矩阵称为“满秩矩阵”,定义域=值域=到达域。说明方阵才可能是满秩矩阵。矩阵A若同时满足行满秩和列满秩,则Ax=b为双射,则映射为一一映射,因此方程Ax=b一定有解,且为唯一解。 逆矩阵满秩矩阵(方阵)双射 矩阵Ax的映射法则:是将标准基用A的列向量(c1,c2)来取代。比如如果c1和c2线性无关则维度保持不变为2,如果c1和c2线性相关则维度小于2.所以基向量c1、c2线性无关是单射,线性相关是非单射。满秩矩阵可以看作是有限个初等矩阵的乘积,一个矩阵经过初等变换,它仍然是同型同秩矩阵。 矩阵列向量线性无关——>列满秩——>值域维度与定义域相同——>单射 矩阵列向量线性相关——>列不满秩——>值域维度降低——>非单射 满射行满秩非单非满射=行不满秩+列不满秩线性方程组Ax=b既不是单射函数,也不是满射函数,可能没有解,也可能是多个解。 对矩阵函数而言,满秩矩阵是双射函数。因此,满秩矩阵存在逆矩阵逆矩阵求法: 1高斯若尔当法 西尔维斯特不等式:r(AB) ≥ r(A) + r(B) - n求矩阵的秩的思路:将矩阵变换为阶梯矩阵形式 线性相关与线性无关 要判断一个向量组是否线性相关,归结为判断齐次线性方程组是否有非零解,若方程组有非零解,则线性相关,否则线性无关。 A为m×n矩阵,则A^TA为可逆方阵的充要条件是,A各列线性无关。 矩阵函数的四个重要概念
总结: 对于m*n的矩阵A的方程Ax=b,rank(A)= rank(B)时有解,且rank(A)=n时有唯一解,当rank(A)特征向量线性无关矩阵A可对角化特征值相同,要判断特征空间的维度 正交阵的定义
☆ 若A,B是正交阵,则A逆是正交阵,A^n 正交阵 ,AB也是正交阵。 施密特正交化得到标准正交基
定义 一个对称矩阵通过转置操作,得到的仍然是它自身,即满足S=S^T,对称矩阵必须是方阵。
性质: 一个矩阵乘以自己的转置矩,即AA^T,得到的结果必然是一个对称矩阵对于任意一个实数对称矩阵,都一定可以被对角化。换句话说,对于一个对称矩阵,无论它的特征值是否重复,它的特征向量都一定线性无关。 实对称矩阵都可以获得一组标准正交的特征向量。任何一个对称矩阵分解得到的特征向量矩阵都可以是标准正交矩阵Q
任意一个 n 阶对称矩阵 S,都可以分解成 n 个秩 1 方阵乘以各自权重系数 λi,然后相加的结果。
既对角又正交的矩阵称对角正交矩阵 充要条件: 对称矩阵可以被对角正交化,矩阵可以被对角正交化也说明矩阵是对称矩阵。
正交阵:A转置=A逆
☆ 实对称矩阵特征值互不相同,对应的特征向量相互正交
这里A为对称矩阵A=A^T,P为正交矩阵p^T=P^-1,也就是说对称矩阵A,一定存在正交矩阵P满足以上对角化公式。 二次型矩阵的性质
二次型的基变换---合同矩阵
标准型:二次型只有二次项,就是二次型的标准型。
用正交变换化二次型成标准形,具有保持几何形状不变的优点
拉格朗日配方法 若二次型含有xi的平方项,则先把含有xi的乘积项集中,然后配方,再对其余的变量同样进行,直到都配成平方项为止。 正定矩阵 如果一个矩阵的所有特征值都为正,我们称它是“正定的”,如果均为非负(即,最小特征值为 0),相当于结论稍稍弱了一些,我们称之为“半正定的”,如果它含有负的特征值,那么它是非正定的。 那么换句话说,对于一个对称矩阵而言,从特征值的正负性角度来看的话,它一定是正定、半正定或非正定的其中一种。 对称矩阵 A^TA的所有特征值都是非负的,特别的,如果矩阵 A 的列向量线性无关,则该矩阵是正定矩阵,特征值均为正。 A^TA和 AA^T 拥有完全一样的非零特征值。
映射后的向量维数和原始向量维数的关系取决于 m 和 n 的关系 如果 m>n,那么目标向量的维数就大于原始向量的维数. 如果 m |
【本文地址】
今日新闻 |
推荐新闻 |