在研究极大似然估计前，先简要阐述下概率与统计的关系

概率 研究的内容是：在已知模型(分布)和参数下，预测某一事件发生的可能性（概率）。

统计 则是根据已经发生的事情或现有数据，通过样本信息统计归纳出模型或者参数。

统计与概率好比 知因求果，知果求因；概率论为统计奠定理论基石，而统计更像一种科学方法（个人理解）；下图是一个比较经典的示意图，已知桶，猜手里；已知手里，归纳桶。

在统计推断中有一个绕不过去的基本问题也是重要问题：参数估计。

那么什么是参数估计呢？===>用样本统计量估计总体参数。可以简单的理解为：当总体参数未知时，从总体抽取样本，用某种方法对这个未知的总体参数进行估计，这就是参数估计。

参数估计又可分为两种：点估计与区间估计。

点估计（point estimate): 就是用样本统计量 \theta 某个取值直接做为总体参数 \theta 的估计值。

举个例子，你想知道全国人口的平均身高吗？第一种方法：查资料；第二种方法：统计所有人身高；第三种方法：抽样统计，每个省份随机抽取1000人，以样本统计量估计总体参数（平均身高）。相信你可以判断出，何种条件下用何种方法。

区间估计（point estimate): 在点估计的基础上，给出总体参数估计的一个区间范围，区间范围通常由样本统计量和估计误差决定.

思考一个问题，为什么有了点估计还要区间估计？相信你已经想到了，因为样本是随机的，抽出一个具体的样本得到的估计值很可能不同于总体真值，所以仅靠点估计有些过于单薄了，说服力度不够，还需要给出点估计的可靠性，但一个点估计的可靠性是由它的抽样标准误差来衡量的，区间估计也就伴随出现了。

矩估计的统计思想：以样本矩估计总体矩，以样本矩的函数估计总体矩的函数。

最简单的矩估计法是用一阶样本原点矩来估计总体的期望而用二阶样本中心矩来估计总体的方差。它是由英国统计学家皮尔逊（Pearson）提出的

1、伯努利（Bernoulli）大数定理：从定义概率的角度，揭示了概率与频率的关系，当试验次数n趋向无穷大的时候，事件A发生的概率等于事件A发生的频率。

前提假设： X_1,X_2,X_3,...,X_n 相互独立且同分布

每次试验A发生的概率为 p， \mu_n 是n重Bernoulli实验中事件A的发生次数

设 $f_n$ 为n重伯努利实验中事件A发生的次数，$p$ 为A在每次实验中发生的概率，当 n 趋向于无穷大的时候，则对任意给定的实数ε>0，有

limP { | \frac{m}{n}-p|< ε } =1

上图模仿了抛硬币试验，从抛1次到抛1000000次，可以发现频率围绕着0.5上下波动并且当试验次数越多时振幅减小。

2、辛钦（Khinchin）大数定律

前提假设:

limP {| {\frac{1}{n}\sum_{i=1}^nX_i-\mu}|< ε}=1

则样本k阶矩 $A_k$ 依概率收敛于 总体阶矩 \mu_k 。可以看出矩估计不涉及分布。

3、切比雪夫（Chebyshev）大数定律：揭示了样本均值和真实期望的关系

前提假设:

limP{|\frac{1}{n}\sum_{i=1}^nX_i-\frac{1}{n}\sum_{i=1}^nEX_i|< \varepsilon }=1 ​ 4、列维-林德伯格（Levi-Lindeberg）定理，独立同分布的中心极限定理

前提假设:

limP\frac{\sum_{i=1}^nX_i-n\mu}{\sqrt n\sigma}< x= \int\frac {1}{\sqrt {2\pi}}e^{-\frac{1}{2}t^2}dt=\phi(x) \\sum_{i=1}^nX_i\sim N(n\mu,n\sigma^2)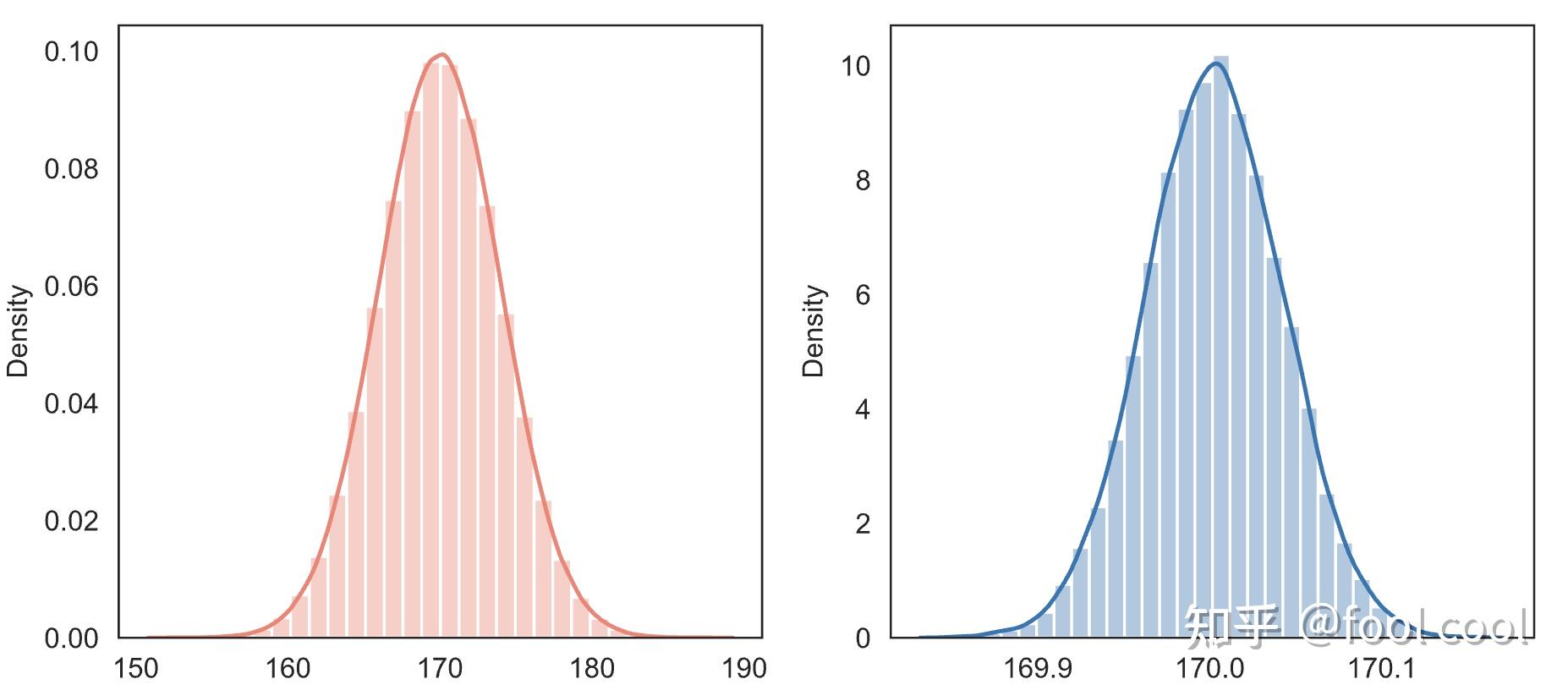

红色图是总体直方图与密度拟合曲线，蓝色图是1000个样本的均值分布图与密度拟合图，结合公式、代码和图片，好好体会一下列维-林德伯格和切比雪夫定理。

​ 极大似然原理： 若事件A发生的概率与参数 $\theta$ 有关， \theta 取值不同则 P(A) 也不同。记事件A发生的概率为 P(A | \theta) . 若一次试验事件A发生了，可认为此时的 \theta 值是在其定义域内 使得 P(A|\theta) 达到最大的那一个，这就是极大似然原理

​ 可理解为：通过样本数据（事后信息），来推导最大概率出现这个事实的模型参数值，通过了解在某一假设下，已知数据发生的可能性，来评价哪一个假设更接近 θ 的真实值。参数值可以有很多，但是我们要找的使这个事件出现的概率是最大的

先看似然函数的定义，它是给定联合样本值 X 下，关于(未知)参数 \theta 的函数： L(\theta|x)=f(x；\theta)

\theta 是指未知参数，它属于参数空间； f(x；\theta) 是概率密度函数。

L(\theta|x) 是关于 \theta 的函数， f(x；\theta) 是关于 x 的函数，所以从定义上解，似然函数和密度函数是完全不同的两个数学对象。公式的等号"=" 理解为函数值形式的相等，而不是两个函数本身是同一函数（根据函数相等的定义，函数相等当且仅当定义域相等并且对应关系相等)。

那么究竟是哪种函数，取决于你已知的信息是 X 还是 \theta ，举个例子 f(x,y)=x^y ，如果 x 已知 f 则是一个指数函数，如果是 y 已知，f则是一个幂函数

L(\theta |x)= \quad\prod_{i=1}^n p(x_i, \theta) 上式为似然函数的表达式，如果是离散分布， p(x_i, \theta) 代表概率质

量函数（概率分布）；如果是连续分布，我们知道连续分布中某一个点的概率为 0，因此需要使用相对应的概率密度函数 f(x ； \theta) 。有了似然函数后，就是求函数的极大极小值了

可能有些小伙伴和我一样对 概率密度函数 是何方神圣感到迷糊，这里简单提及一下

概率密度函数不表示概率，而是表示概率分布的密集程度，是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。而随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分。

左边图表示pdf（概率密度函数），右边图表随机变量取值分布。如左图，在0时，函数值最大，对应右图变量的取值也是最多的，即分布更加密集。

参考资料：如何理解似然函数

已经做好了铺垫，现在要真正来了解MLE了。

​ 有一个抛硬币的游戏，庄家说这枚硬币质地均匀，大家可以放心的参与进来，输赢全凭运气。张三准备玩1000把，每次都压1元给反面，心想我学过数学，根据大数定律，最后输赢不大，可以玩玩。最后结果是800次正面、200次反面，净亏损6000元。学过概率论的他觉得哪里不对，难道被骗了，于是心里开始琢磨

此处将试验看成为伯努利分布（一个样本，含10000次试验）

L(θ) = \quad\prod_{i=1}^nP(X=x_i|θ）=θ^{800}*(1-θ)^{200}

对上式取对数 ln(L(θ))= 800ln(θ)+200ln(1-θ)

对上述进行求导，令其倒数为0求得到其驻点 ：

lnL(θ)'=\frac {8000}{θ} - \frac{2000}{({1-θ})}=0

解得 θ =0.8.

L(\theta) 表示 在参数 \theta 下，该事件出现的可能性，不同的参数取值， 事件的发生概率也不一样。下图描述了似然函数值随参数的变化

可以看到在参数值取0.8时，事件发生的概率最大，因此认为硬币抛出正面概率为0.8时，出现该实验结果的可能性最大。

​ 这时庄家可能会反驳，铸币厂铸造的硬币一般都是均匀的，就算现在的结果是8000正面2000反面，我也不信硬币不是均匀的，休想诬陷我（θ等于0.8）。

这里就包含一些贝叶斯学派的思想了，考虑先验概率即先验信息，因此便引入了最大后验概率估计（Maximum A Posteriori estimation）。

这里提下统计学的两大学派 频率学派 与 贝叶斯学派 ，两种学派的主要差别在于探讨 不确定性 这件事儿的视角不一样，因此他们对于产生数据的模型参数的理解也不同，总之二者相爱相杀，相互成长。

Fisher是频率学派的代表人之一，也是他提出的极大似然估计。他们认为事件本身就具有客观的不确定性，直接为事件本身建模，也就是说事件在多次重复实验中趋于一个稳定的值p，那么这个值就是该事件的概率。他们认为模型参数是个定值，希望通过类似解方程组的方式从数据中求得该未知数。这就是频率学派使用的参数估计方法：极大似然估计（MLE），这种方法往往在大数据量的情况下可以很好的还原模型的真实情况。

贝叶斯学派不去试图解释 事件本身的随机性，而是从观察者角度出发，认为不确定性来源于观察者的知识不完备，在这种情况下，通过已经观察到的信息来描述最有可能推导的过程。因此，同一件事情对于知情者而言就是【确定事件】，对于不知情者而言就是【随机事件】，随机性并不源于事件本身是否发生，而只是描述观察者对该事件的知识状态。

他们认为模型参数源自某种潜在分布（个人认为：一切的统计、数据挖掘等都必须有个前提，世界是规律的运行），希望从数据中推知该分布。对于数据的观测方式不同或者假设不同，那么推知的该参数也会因此而存在差异。这就是贝叶斯派视角下用来估计参数的常用方法-最大后验概率估计（MAP），这种方法在先验假设比较靠谱的情况下效果显著，随着数据量的增加，先验假设对于模型参数的主导作用会逐渐削弱，相反真实的数据样例会大大占据有利地位。极端情况下，比如把先验假设去掉，或者假设先验满足均匀分布的话，那它和极大似然估计就如出一辙了。

条件概率公式： P(A|B) = \frac{P(A,B)}{P(B)} 全概率公式：将对一复杂事件A的概率求解问题转化为了在不同情况下发生的简单事件的概率的求和问题。

原理：如果事件B1、B2、B3…Bn 构成一个完备事件组，即它们两两互不相容，其和为全集；并且 P(B_i) 大于0，则对任一事件A有 ：

P(A)=P(A,B_1)+(A,B_2)+P(A,B_n)=P(A|B_1)P(B_1)+P(A|B_2)P(B_2)... + P(A|B_n)P(B_n)

其实是将事件A与一个全集B分解成多个A的子集与B的子集的交集。

贝叶斯公式：知果推因

假设村里自行车丢的概率是0.2（事件A），村里一共有20个人，张三、李四王五曾经偷窃过，也就是B1、B2、B3的行窃概率是0.2，0.3，0.5，行窃成功率分别是0.7，0.8，0.9。那么警察先调查谁的概率最大。

P(B_i|A)=\frac{P(A,B_i)}{P(A)}=\frac{P(A|B_i)*P(B_i)}{P(A,B1)+(A,B2)+P(A,B_3)}

P(B_i|A) =\frac{P(A|B_i)*P(B_i)}{P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+P(A|B_3)P(B_3)}

贝叶斯公式是对条件概率公式和全概率公式进行一个综合运用，当然他们必须得满足前提条件，独立。

OK，终于介绍完了事前准备内容，直接进入最大后验概率估计。

回到上文的抛硬币案例，MLE是求参数θ的值，使得似然函数P(x|θ)最大；MAP希望θ不仅使似然函数最大，同时也希望θ本身出现的先验概率也最大。

MAP=》max(P(θ|X=x)=\frac{P(X=x|θ)*P(θ)}{P(X=x)}

公式里面的 P(θ) 是指概率密度函数（也可以是概率质量函数）

由于， P(X=x) 这一试验结果已经产生，我们这里暂且不管它，认为是一个确定的常量 $C$， 等价于求解

arg_{\theta}max {P(X=x|θ)P(θ)}

arg_{\theta} MAX[{P(X=x|θ)P(θ)}]

这里我们根据先验经验，假设 \theta 服从 均值为0.5的，方差为0.01的正态分布（用beta分布来拟合更加合理），也就是说，认为硬币抛正面的概率是0.5最大，但也可能是其他值

模拟实验发现， \theta 的取值为0.8，最大后验概率函数取值最大，因此认为抛正面的概率为0.8。

最后的疑惑可能是，有人会问：你为什么知道参数 \theta 是服从正态分布啊？我们把铸币厂铸币生产看成一个总体，从中抽取样本，根据中心极限定理，我们的均值抽样分布是服从高斯分布的。更为严谨的是用Beta分布来拟合，Beta分布是描述概率的概率分布，我这里偷懒直接整成高斯分布了（还没完全懂beta分布）

极大似然估计与最大后验概率估计的区别在于 对于先验信息的了解程度，如果忽略模型（参数）本身的概率的分布，或者认为参数服从0-1均匀分布，那么最大后验概率估计将弱化为最大似然估计。

参考资料：

极大似然估计原理：https://www.cnblogs.com/LittleHann/p/7823421.html

如何理解beta分布：https://www.zhihu.com/question/30269898

好了，文章到这儿就暂告一段落了，本文主要目的是想让大家初步了解什极大似然估计的原理和应用。如果文章内容对你有帮助，我将万分欣喜，同时欢迎您的转发、评论、点赞、收藏。

对于文章内容，笔者会尽力做到严谨，如果有小伙伴发现语义混乱或者解释错误的地方，还请不吝指教，我将不胜感激并及时改正。

stay hungry, stay foolish , 与君共勉.