卷积神经网络优化论文 |
您所在的位置:网站首页 › 卷积神经网络优化算法 › 卷积神经网络优化论文 |
卷积神经网络优化论文
|
1 卷积神经网络是什么?
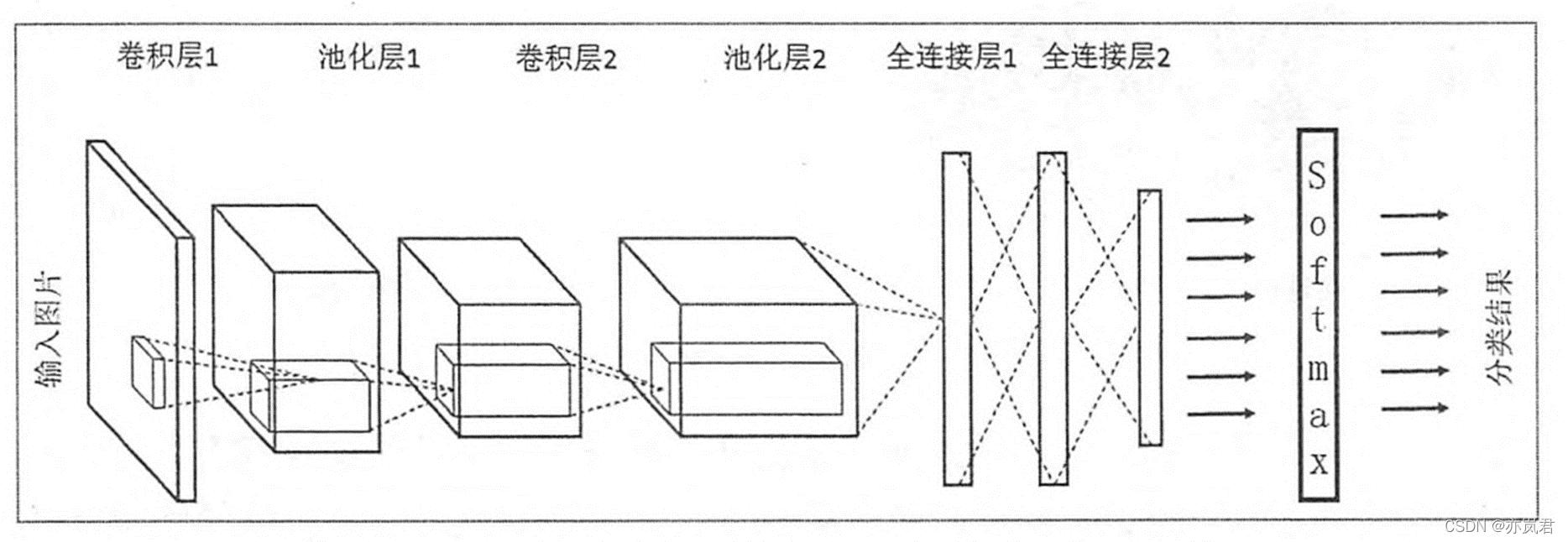
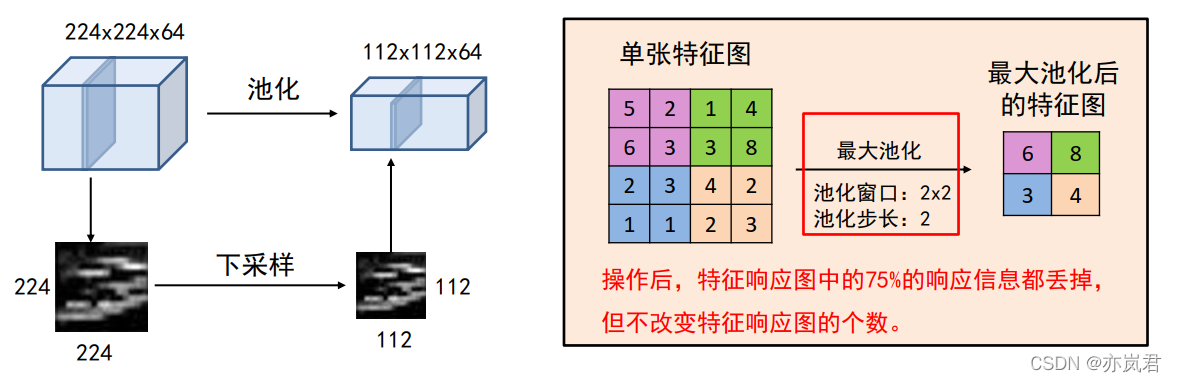
卷积神经网络(Convolution Neural Network)可以简单理解为包含卷积操作且具有深度结构的网络,通过权值共享和局部连接的方式对数据进行特征提取并进行预测的过程。在实际应用中往往采用多层网络结构,因此又被称为深度卷积神经网络。卷积神经网络通过反馈修正卷积核和偏置参数使输出与预测偏差减小。所以,构建卷积神经网络进行深度学习开发其实并不复杂。可以从四个方面展开:输入输出、网络结构、损失函数、评价指标。 2 卷积神经网络的输入输出卷积神经网络的输入分为两部分,一是数据,二是标签。针对计算机视觉任务来说,通常数据指的是图像数据。标签是针对图像的真实值,针对不同任务有着不同的标签,例如图像分类任务的标签是图像的类别,目标检测任务的标签是图像中的目标的类别和坐标信息等。这类标签信息一般通过人工标定方式(或者自动标定工具)生成。例如VIA标注工具。 3、卷积神经网络的网络结构卷积神经网络的基本结构由以下几个部分组成:输入层(input layer),卷积层(convolution layer),池化层(pooling layer),激活函数层和全连接层(full-connection layer)。下面以图像分类任务简单介绍一下卷积神经网络结构,具体结构如下图所示。 图像分类任务是输入层是 H ∗ W ∗ C H*W*C H∗W∗C的图像,其中H是指图像的长度,W是图像的宽度,C指的是图像的channel数,一般灰度图的channel数为1,彩色图的channel数为3。 3.2 卷积层卷积神经网络的核心是卷积层,卷积层的核心部分是卷积操作。 卷积层有四个重要的超参数:卷积核的大小F、卷积核的个数K、卷积的步长S和零填充数量P。 假设输入的参数为: H × W × D H×W×D H×W×D的一个Tensor,则经过一个大小为、个数为K,步长为S和零填充数量为P的卷积操作后输出的参数为: H ′ = ( H − F + 2 P ) / S + 1 W ′ = ( W − F + 2 P ) / S + 1 D ′ = K \begin{matrix}H' = (H-F+2P)/S+1 \\W' = (W-F+2P)/S+1 \\ D'=K \end{matrix} H′=(H−F+2P)/S+1W′=(W−F+2P)/S+1D′=K 关于卷积计算可以参考这篇文章,我的下面图片就引自该问文,链接: 原来卷积是这么计算的_月来客栈。 其中卷积层的操作可分为四种,分别为: 单输入单输出(输入channel数为1,且只有1个卷积核)单输入多输出(输入channel数为1,并有n(n>1)个卷积核)多输入单输出(输入channel数>1,只有1个卷积核)多输入多输出(输入channel数>1,并有n(n>1)个卷积核) 3.2.1 单输入单输出channel数为1的图像的单一卷积核的计算过程如下图所示: 池化操作将输入矩阵某一位置相邻区域的总体统计特征作为该位置的输出,主要有平均池化(Average Pooling)、最大池化(Max Pooling)等。卷积的作用为:对每一个特征响应图独立进行, 降低特征响应图组中每个特征响应图的宽度和高度,减少后续卷积层的参数的数量, 降低计算资源耗费,进而控制过拟合,简单来说池化就是在该区域上指定一个值来代表整个区域。 池化层的超参数:池化窗口和池化步长。 池化操作也可以看做是一种卷积操作,下面我们以最大池化来解释池化操作,具体操作如下图所示: 激活函数(非线性激活函数,如果激活函数使用线性函数的话,那么它的输出还是一个线性函数。)但使用非线性激活函数可以得到非线性的输出值。常见的激活函数有Sigmoid、tanh和Relu等。一般我们使用Relu作为卷积神经网络的激活函数。 Relu激活函数提供了一种非常简单的非线性变换方法,它的公式为:
f
(
u
)
=
m
a
x
(
0
,
u
)
f(u)= max(0,u)
f(u)=max(0,u) 函数图像如下所示: 全连接层在卷积神经网络中起到分类器的作用,如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话,全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。 3 卷积神经网络的损失函数在卷积神经网络中,我们会使用如梯度下降法(Gradient Descent) 等方法去最小化目标函数。但怎样来衡量优化目标函数的好坏呢,这就用到了损失函数。卷积神经网络中损失函数是用于衡量模型所作出的预测值和真实值(Ground Truth)之间的偏离程度,大致可分为两种:分类损失(针对离散型量)和回归损失(针对连续型变量)。 3.1分类损失 3.1.1 熵(Entropy)即“熵”,熵的概念最早起源于物理学,用于度量一个热力学系统的无序程度。在信息论里面, 熵是用于描述对事件不确定性的度量,它的计算公式如下:
E
n
t
r
o
p
y
,
H
(
p
)
=
−
Σ
p
(
x
i
)
∗
l
o
g
2
(
p
(
x
i
)
)
Entropy,H(p) = -\varSigma p(x_i)*log_2(p(x_i))
Entropy,H(p)=−Σp(xi)∗log2(p(xi)) 其中
p
(
i
)
p(i)
p(i)为事件的概率分布,下面以一个例子来解释一下该公式。 假设气象台告知我们明天晴天的概率为25%,下雨的概率为75%,则气象站传输给我们的信息熵为:
−
(
0.25
∗
l
o
g
2
(
0.25
)
+
0.75
∗
l
o
g
2
(
0.75
)
)
=
0.81
-(0.25*log2(0.25) + 0.75*log2(0.75)) =0.81
−(0.25∗log2(0.25)+0.75∗log2(0.75))=0.81 如下图所示: 相对熵又称KL散度,用于衡量对于同一个随机变量x的两个分布p(x)和q(x)之间的差异。在机器学习中,p(x)常用于描述样本的真实分布,例如[1,0,0,0]表示样本属于第一类,而q(x)则常常用于表示预测的分布,例如[0.7,0.1,0.1,0.1]。显然使用q(x)来描述样本不如p(x)准确,q(x)需要不断地学习来拟合准确的分布p(x)。 KL散度的计算公式为: D K L ( p ∣ ∣ q ) = ∑ i = 1 n p ( x i ) l o g 2 ( p ( x i ) q ( x i ) ) D_{KL}(p||q) = \displaystyle\sum_{i=1}^n p(x_i) log_2(\frac {p(x_i)} {q(x_i)}) DKL(p∣∣q)=i=1∑np(xi)log2(q(xi)p(xi)) KL散度的值越小表示两个分布越接近。 3.1.3 交叉熵(Cross Entropy)我们将KL散度的公式进行变形,得到: D K L ( p ∣ ∣ q ) = ∑ i = 1 n p ( x i ) l o g 2 ( p ( x i ) ) − ∑ i = 1 n p ( x i ) l o g 2 ( q ( x i ) ) = − H ( p ( x ) ) + [ − ∑ i = 1 n p ( x i ) l o g 2 ( q ( x i ) ) ] D_{KL}(p||q) = \displaystyle\sum_{i=1}^n p(x_i) log_2(p(x_i))- \displaystyle\sum_{i=1}^n p(x_i) log_2(q(x_i)) =-H(p(x))+[-\displaystyle\sum_{i=1}^n p(x_i) log_2(q(x_i))] DKL(p∣∣q)=i=1∑np(xi)log2(p(xi))−i=1∑np(xi)log2(q(xi))=−H(p(x))+[−i=1∑np(xi)log2(q(xi))] 前半部分就是p(x)的熵,它是一个定值,后半部分就是我们的交叉熵: C r o s s E n t r o p y , H ( p , q ) = − ∑ i = 1 n p ( x i ) l o g 2 ( q ( x i ) ) Cross Entropy,H(p,q) = -\displaystyle\sum_{i=1}^n p(x_i) log_2(q(x_i)) CrossEntropy,H(p,q)=−i=1∑np(xi)log2(q(xi)) 我们常常使用KL散度来评估predict和label之间的差别,但是由于KL散度的前半部分是一个常量,所以我们常常将后半部分的交叉熵作为损失函数。假设我们当前做一个3个类别的图像分类任务,如猫、狗、猪。给定一张输入图片其真实类别是猫,模型通过训练用Softmax分类后的输出结果为:{“cat”: 0.3, “dog”: 0.45, “pig”: 0.25},那么此时交叉熵为:-1 * log(0.3) = 1.203。当输出结果为:{“cat”: 0.5, “dog”: 0.3, “pig”: 0.2}时,交叉熵为:-1 * log(0.5) = 0.301。可以发现,当预测值接近真实值时,损失将接近0。 3.2 回归损失(Regression Loss) 3.2.1 L1损失也称为Mean Absolute Error,即平均绝对误差(MAE),它衡量的是预测值与真实值之间距离的平均误差幅度,作用范围为0到正无穷。其公式如下: l o s s = ∑ i = 1 n ∣ y i − y ^ i ∣ loss = \displaystyle\sum_{i=1}^n|y_i - \hat y_i| loss=i=1∑n∣yi−y^i∣ 3.2.2 L2损失也称为Mean Squred Error,即均方差(MSE),它衡量的是预测值与真实值之间距离的平方和,作用范围同为0到正无穷。其公式如下: l o s s = ∑ i = 1 n ( y i − y ^ i ) 2 loss = \displaystyle\sum_{i=1}^n(y_i - \hat y_i)^2 loss=i=1∑n(yi−y^i)2 3.2.3 L1与L2损失函数对比L1损失函数相比于L2损失函数的鲁棒性更好,因为L2将误差平方化(如果误差大于1,则误差会放大很多),模型的误差会比L1范数大的多,因此模型会对这种类型的样本更加敏感,这就需要调整模型来最小化误差。 但L2收敛速度快,能够对梯度给予合适的惩罚权重,而不是“一视同仁”,使梯度更新的方向可以更加精确。 3.2.4 Smooth L1损失即平滑的L1损失(SLL),出自Fast RCNN。SLL通过综合L1和L2损失的优点,在0点处附近采用了L2损失中的平方函数,解决了L1损失在0点处梯度不可导的问题,使其更加平滑易于收敛。此外,在|x|>1的区间上,它又采用了L1损失中的线性函数,使得梯度能够快速下降。 s m o o t h L ( x ) = x = { 0.5 x 2 if ∣ x ∣ < 1 ∣ x ∣ − 0.5 otherwise smooth_L(x) = x = \begin{cases} 0.5x^2 &\text{if } |x| |
【本文地址】
今日新闻 |
推荐新闻 |
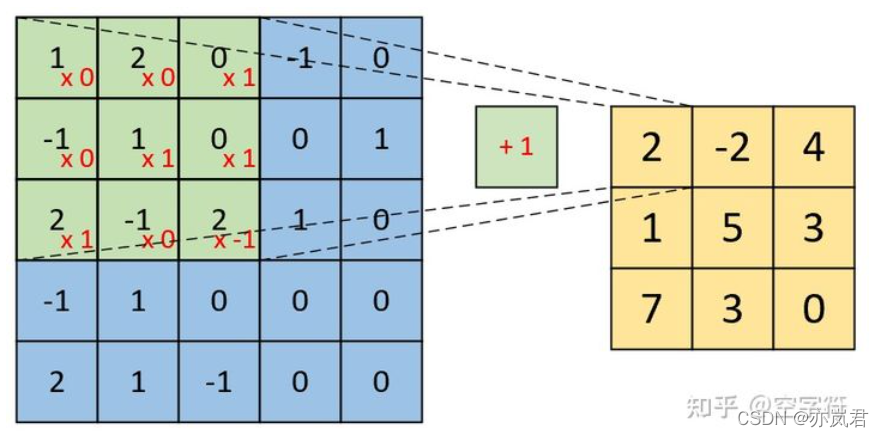 具体计算过程如下图:
具体计算过程如下图: 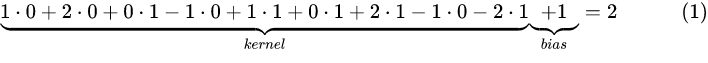 channel数为3的图像的单一卷积核的计算过程如下图所示:
channel数为3的图像的单一卷积核的计算过程如下图所示: 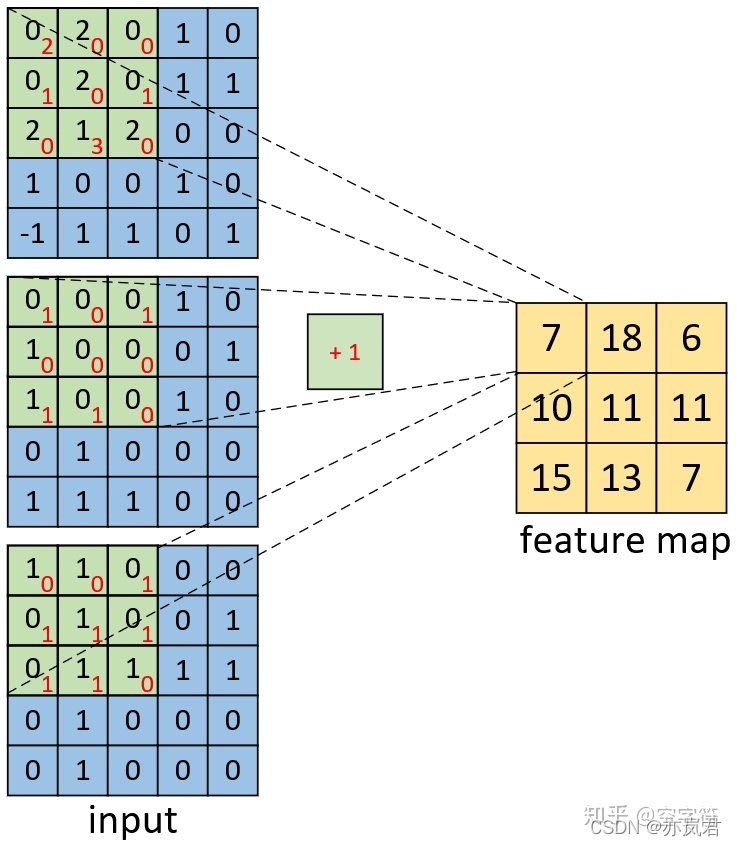 具体计算过程如下图:
具体计算过程如下图:  channel数为3的图像的多卷积核的计算过程如下图所示:
channel数为3的图像的多卷积核的计算过程如下图所示: 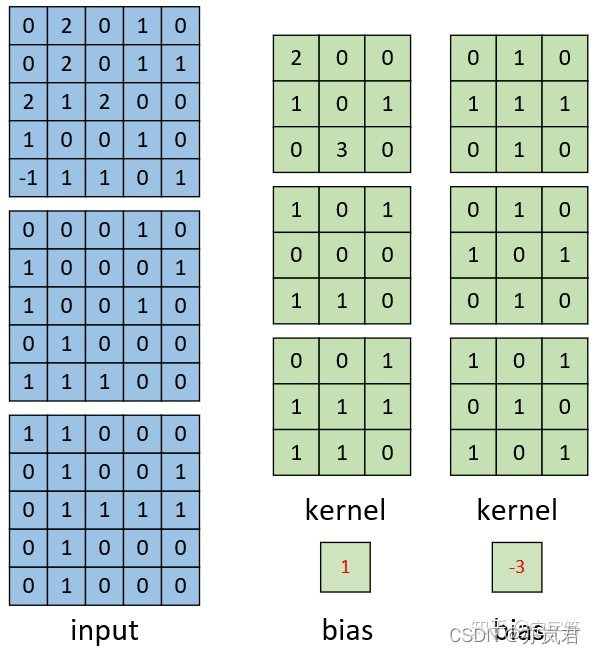 计算得到的结果如下图:
计算得到的结果如下图: 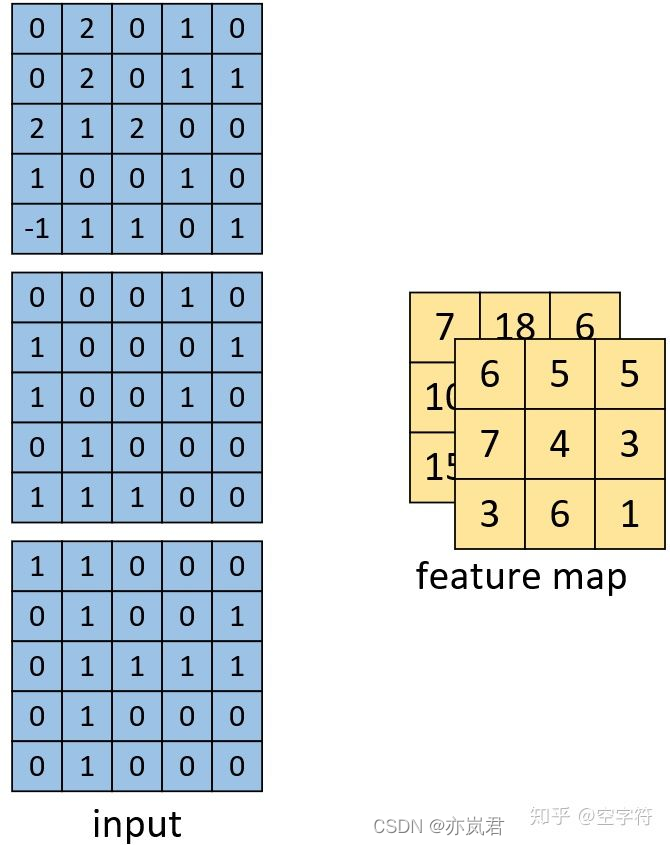
 ReLU激活函数相比Sigmoid、tanh等有的优点为: 1、速度快,和sigmoid函数需要计算指数和倒数相比,relu函数其实就是一个
m
a
x
(
0
,
u
)
max(0,u)
max(0,u),计算代价小。 2、稀疏性,通过对大脑的研究发现,大脑在工作的时候只有大约5%的神经元是激活的,而采用sigmoid激活函数的激活率大约是50%。有论文声称人工神经网络在15%-30%的激活率时是比较理想的。因为Relu函数在输入小于0时是完全不激活的,因此可以获得一个更低的激活率。 3、ReLU的求导特性也非常的好。当输⼊为负时, ReLU函数的导数为0,⽽当输⼊为正时, ReLU函数的导数为1。这就意味着要么让参数消失,要么让参数通过。并且ReLU减轻了困扰以往神经⽹络的梯度消失问题。 注意: ReLU函数有许多变体,包括参数化ReLU(Parameterized ReLU, pReLU)函数。该变体为ReLU增减了一个线性项,因此即使参数是负的,某些信息仍然可以通过:
p
R
e
L
U
=
m
a
x
(
0
,
x
)
+
α
m
i
n
(
0
,
x
)
pReLU = max(0,x)+\alpha min(0,x)
pReLU=max(0,x)+αmin(0,x)
ReLU激活函数相比Sigmoid、tanh等有的优点为: 1、速度快,和sigmoid函数需要计算指数和倒数相比,relu函数其实就是一个
m
a
x
(
0
,
u
)
max(0,u)
max(0,u),计算代价小。 2、稀疏性,通过对大脑的研究发现,大脑在工作的时候只有大约5%的神经元是激活的,而采用sigmoid激活函数的激活率大约是50%。有论文声称人工神经网络在15%-30%的激活率时是比较理想的。因为Relu函数在输入小于0时是完全不激活的,因此可以获得一个更低的激活率。 3、ReLU的求导特性也非常的好。当输⼊为负时, ReLU函数的导数为0,⽽当输⼊为正时, ReLU函数的导数为1。这就意味着要么让参数消失,要么让参数通过。并且ReLU减轻了困扰以往神经⽹络的梯度消失问题。 注意: ReLU函数有许多变体,包括参数化ReLU(Parameterized ReLU, pReLU)函数。该变体为ReLU增减了一个线性项,因此即使参数是负的,某些信息仍然可以通过:
p
R
e
L
U
=
m
a
x
(
0
,
x
)
+
α
m
i
n
(
0
,
x
)
pReLU = max(0,x)+\alpha min(0,x)
pReLU=max(0,x)+αmin(0,x) 在卷积神经网络中,比如分类任务中,其实也是在做一个判断一个物体到底是不是属于某个类别,其中不确定性就越大,其信息量越大,它的熵值就越高。
在卷积神经网络中,比如分类任务中,其实也是在做一个判断一个物体到底是不是属于某个类别,其中不确定性就越大,其信息量越大,它的熵值就越高。