卷积作用是为了进行特征提取 因为输入的信息中可能只有一小部分是对我们解决问题有帮助的，这些信息比较关键，这时候只提取这部分信息就可以了。 比如下面我们有以下图片数据，我们现在的任务是对衣服的款式进行判断，判断它是上衣还是裤子，或者是裙子 那对于这个任务来说，颜色这个信息就不重要，我们不需要通过颜色来判断一个衣服是上衣还是裤子，比如一个黑白的图片我们也完全可以判断。这时候就需要把这个信息过滤掉，只留下对判断款式有用的信息，比如轮廓： 这其实就是进行了卷积运算，可以看到它提取到了轮廓这个特征，虽然对于人来说彩色的看着更舒服，但是对于计算机来说，进行特征提取后，需要处理的信息就急剧减少，可以极大的加快运行速度，当然这只是我认为其中比较重要的一个原因，使用卷积+池化还有其他的作用，需要详细研究的可以看这篇文章，写的非常详细： 一文看懂卷积神经网络-CNN

提取特征，也就是只保留我们想要的信息，去除不需要的信息，相当于电路中的滤波器。 我第一次知道卷积这个名词是大学课程《信号与系统》中来的，这里我们需要了解有关卷积的知识只需要以下3条就行了：

数学中卷积的定义： 连续： ( f ∗ g ) ( n ) = ∫ − ∞ ∞ f ( τ ) g ( n − τ ) d τ (f*g)(n)=\int_{-\infty}^\infty{f(\tau)g(n-\tau)d\tau} (f∗g)(n)=∫−∞∞​f(τ)g(n−τ)dτ 离散： ( f ∗ g ) ( n ) = ∑ τ = − ∞ ∞ f ( τ ) g ( n − τ ) d τ (f*g)(n)=\sum_{\tau=-\infty}^\infty{f(\tau)g(n-\tau)d\tau} (f∗g)(n)=∑τ=−∞∞​f(τ)g(n−τ)dτ

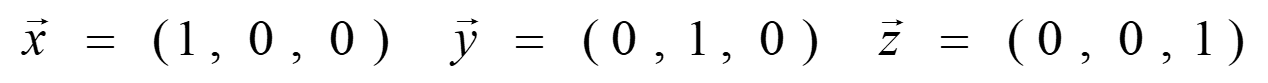连续信号的卷积运算因为需要积分，所以计算量比较大，因此可以通过傅里叶变换后转到频域，直接相乘，然后再逆傅里叶变换回去就完成卷积计算了。虽然离散信号因为是累加，计算量并不大，不需要傅里变换，但是从频域分析会更好理解卷积进行特征提取的原理，所以我们下面对离散信号也做傅里叶变换： 比如我们有一个原始信号 f {f} f 卷积核 g {g} g ， f {f} f 就相当于图片的像素组成的矩阵， g {g} g 就是卷积核，也是一个矩阵。 为了描述简单，我们现在把 f {f} f 和 g {g} g 都看作向量 现在我们有一个两两正交的三维空间 假如 f f f（时域信号） 映射到(即傅里叶变换后)此空间上后为 f ^ \hat{f} f^​（频域信号）， f ^ \hat{f} f^​在 x ⃗ \vec{x} x 和 y ⃗ \vec{y} y ​ 上不为0 g g g 映射到此空间后为 g ^ \hat{g} g^​， g ^ \hat{g} g^​在 x ⃗ \vec{x} x 上不为0，在 x ⃗ \vec{x} x 和 z ⃗ \vec{z} z 上为0 即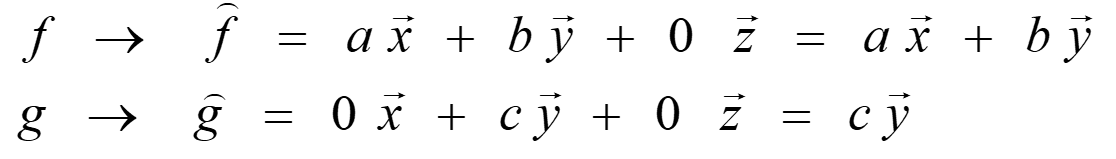： 那么此时对映射后（即傅里叶变换后）的向量进行相乘 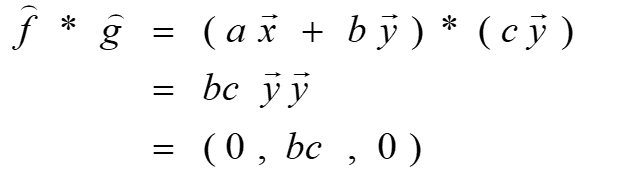会发现，相乘后只有y上有值，因为f和g都在y上映射长度不为0 所以： 我们知道滤波器有高通滤波，低通滤波，所谓的高通滤波就是只有高频率的波通过，滤除低频率的波，低通滤波反之。那在我们这里，对f来说，卷积操作就像是一个 g通滤波，只有g中有的分量，f才能通过。滤除没有g的信息，留下有g的信息，这就是特征提取，起到作用就是提取g这个特征。