α\alphaα 衰变 是原子核自发放射出 α\alphaα 粒子发生转变的过程。是三种天然放射性之一。 α\alphaα 衰变具有以下特征：

Fig：α\alphaα衰变

α\alphaα 衰变可表示为：

ZAX→Z−2A−4Y+24He\mathrm{^A_ZX} \rightarrow \mathrm{^{A-4}_{Z-2}Y} + \mathrm{^4_2He} ZA​X→Z−2A−4​Y+24​He

即母核 XXX 发生 α\alphaα 衰变产生 α\alphaα 粒子与子核 YYY。

1930 年以前，人们认为从同一种原子核中发射出来的 α\alphaα 粒子的能量是一样的，没有发现“精细结构”。这是当时的实验手段受到限制（直接测量 α\alphaα 粒子在空气中的射程）。随着技术的发展，有很多高精度的测量方式被发展出来。下面对 磁谱仪 的原理作简单介绍。

磁谱仪是利用磁场来测定带电粒子能量的装置。下图是一种半圆谱仪的工作原理图。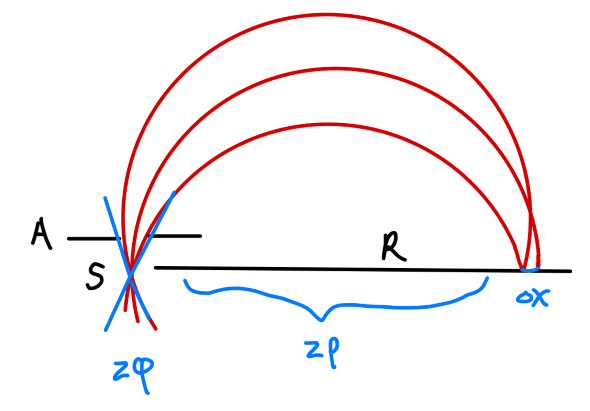

Fig：半圆谱仪的工作原理图

放射源 SSS，感光胶片 RRR 和限束光栏 AAA 都放在一个扁平的真空盒里。从放射源发出的带电粒子束被限束光栏限制在 2φ2\varphi2φ 的角度内。在垂直于真空盒的方向上加一磁场，使得带电粒子发生偏转。相同能量的 α\alphaα 粒子应当打在感光片同一位置上。有：

mv2ρ=qvB⇒p=mv=qBρ(1)\frac{mv^2}{\rho} = qvB\Rightarrow p =mv = qB\rho \tag{1} ρmv2​=qvB⇒p=mv=qBρ(1)

考虑到源对狭缝的张角 2φ2\varphi2φ 不可能无限小，这导致谱线存在一定宽度。有：

Δx=ρφ2(2)\Delta x = \rho\varphi^2 \tag{2} Δx=ρφ2(2)

这决定了半圆谱仪的分辨本领。

对于寿命很长的辐射体，利用磁谱仪来进行研究是很困难的，因为磁谱仪对于源的利用率很低。此时，我们一般采用半导体探测器或气体探测器。

在用磁谱仪对 α\alphaα 放射源的测量结果表明，α\alphaα 粒子的能量并不单一，而是有几种不同的能量数值。在 α\alphaα 谱的精细结构中，一般只有一种能量的 α\alphaα 粒子强度较强。其他 α\alphaα 粒子的强度较弱，其中能量较低、射程较短的为 短射程 α\alphaα 粒子；其中能量较高、射程较长的为 长射程 α\alphaα 粒子（少数核素存在）。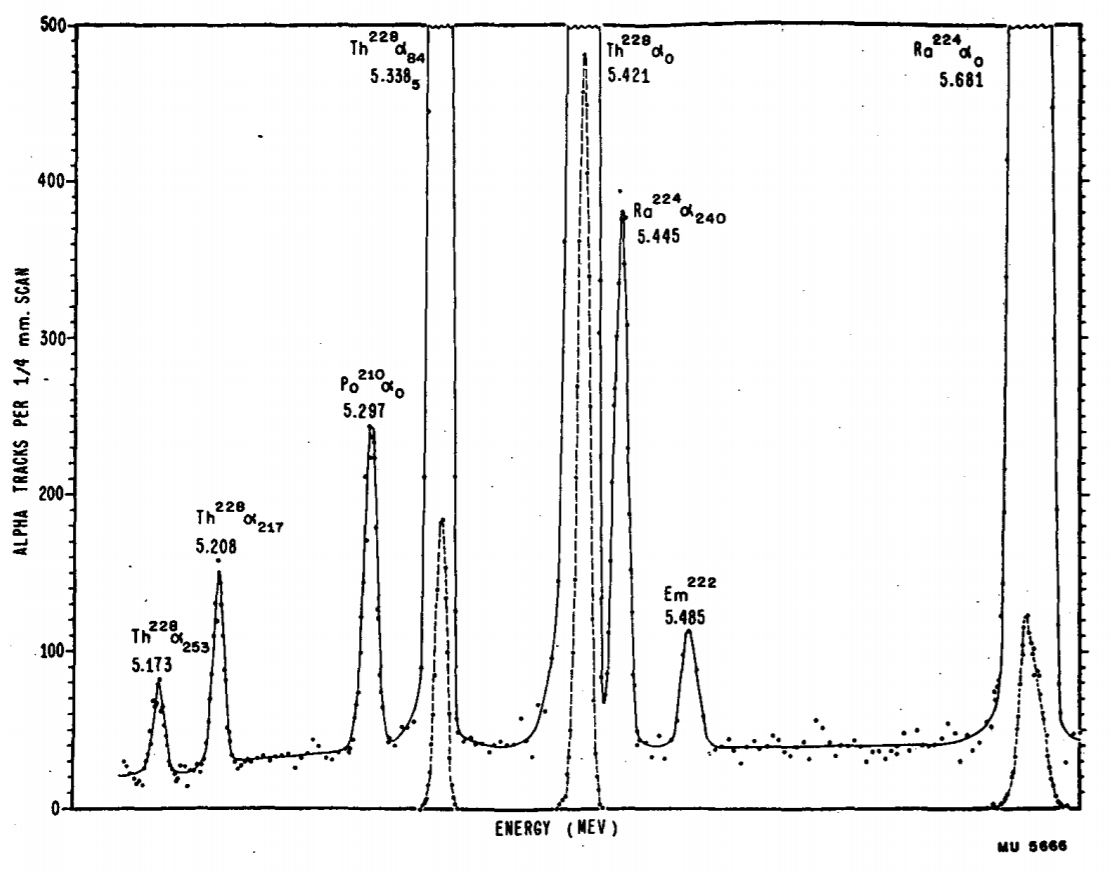

Fig：α 能谱的精细结构[2]^{[2]}[2]

短射程 α\alphaα 粒子与长射程 α\alphaα 粒子的产生与原子核不同的能级结构有关。

短射程 α\alphaα 粒子 原子核 ZAX\mathrm{^A_ZX}ZA​X 放出 α\alphaα 粒子衰变为原子核 Z−2A−4Y\mathrm{^{A-4}_{Z-2}Y}Z−2A−4​Y 时，衰变到 Y\mathrm{Y}Y 的激发态。

长射程 α\alphaα 粒子 处于激发态的母核 ZAX\mathrm{^A_ZX}ZA​X 放出 α\alphaα 粒子衰变为原子核 Z−2A−4Y\mathrm{^{A-4}_{Z-2}Y}Z−2A−4​Y 时，衰变到 Y\mathrm{Y}Y 的基态。这种情况下，母核往往是衰变的产物。且激发态即可以通过 α\alphaα 衰变，也可以通过 γ\gammaγ 衰变回到基态，这取决于两种过程的分支比。一般来说，发生 γ\gammaγ 衰变的概率大的多，只有少部分核素发生 α\alphaα 衰变的几率才相对较大（尽管绝对数值也很小）。在天然放射性核素中只有 84212Po\mathrm{^{212}_{84}Po}84212​Po 和 84214Po\mathrm{^{214}_{84}Po}84214​Po 有长射程 α\alphaα 粒子。

α\alphaα 衰变能 是指 α\alphaα 衰变时放出的能量。该能量为 α\alphaα 粒子的动能与子核粒子动能的总和。

α\alphaα 衰变表示为：

ZAX→Z−2A−4Y+24He\mathrm{^A_ZX} \rightarrow \mathrm{^{A-4}_{Z-2}Y} + \mathrm{^4_2He} ZA​X→Z−2A−4​Y+24​He

衰变能为：

Ed=(mX−mY−mα)c2=Ek+ER(3)E_d = (m_X-m_Y - m_{\alpha})c^2 = E_k + E_R \tag{3} Ed​=(mX​−mY​−mα​)c2=Ek​+ER​(3)

Ek,ERE_k,E_REk​,ER​ 分别为 α\alphaα 粒子与子核的动能。假设衰变前母核是静止的，根据动量守恒得到：

mYvY+mαvα=0(4)m_Yv_Y + m_{\alpha}v_{\alpha} = 0 \tag{4} mY​vY​+mα​vα​=0(4)

由此得到 α\alphaα 粒子动能与衰变能的关系：

Ek=A−4AEd;ER=4AEd(5)E_{k} = \frac{A-4}{A} E_d;\quad E_{R} = \frac{4}{A} E_d \tag{5} Ek​=AA−4​Ed​;ER​=A4​Ed​(5)

自发发生 α\alphaα 衰变的核素的质量数通常在 200200200 以上，那么对应的 α\alphaα 粒子动能约占衰变能的 98%98\%98%。反冲能约为 2%2\%2%。

衰变能随原子序数和质量数的关系

实验表明，并不是所有的原子核都能够发生 α\alphaα 衰变。确切来说，只有 A>140A>140A>140 的核素才能发生 α\alphaα 衰变。现在来讨论这个问题。

对于 α\alphaα 衰变：

ZAX→Z−2A−4Y+24He\mathrm{^A_ZX} \rightarrow \mathrm{^{A-4}_{Z-2}Y} + \mathrm{^4_2He} ZA​X→Z−2A−4​Y+24​He

考虑上述衰变过程中每个粒子的质量亏损：

{ΔmX=Zmp+(A−Z)mn−mXΔmY=(Z−2)mp+(A−Z−2)mn−mYΔmα=2mp+2mn−mα(6)\left\{ \begin{aligned} & \Delta m_X = Zm_p + (A-Z)m_n - m_X\\ & \Delta m_Y = (Z-2)m_p + (A-Z-2)m_n - m_Y\\ & \Delta m_\alpha = 2m_p + 2m_n - m_\alpha\\ \end{aligned} \tag{6} \right. ⎩⎪⎨⎪⎧​​ΔmX​=Zmp​+(A−Z)mn​−mX​ΔmY​=(Z−2)mp​+(A−Z−2)mn​−mY​Δmα​=2mp​+2mn​−mα​​(6)

于是衰变能可以写作：

Ed=(ΔmY+Δmα−ΔmX)c2=BY+Bα−BX(7)\begin{aligned} E_d &= (\Delta m_Y + \Delta m_\alpha - \Delta m_X)c^2\\ &=B_Y + B_{\alpha} -B_X\\ \end{aligned}\tag{7} Ed​​=(ΔmY​+Δmα​−ΔmX​)c2=BY​+Bα​−BX​​(7)

若假设 BBB 随 Z,AZ,AZ,A 的变化时平滑的，那么我们将衰变能近似表示为：

Ed≈∂B∂ZΔZ+∂B∂AΔA+Bα(8)E_d \approx \frac{\partial B}{\partial Z}\Delta Z + \frac{\partial B}{\partial A}\Delta A + B_\alpha \tag{8} Ed​≈∂Z∂B​ΔZ+∂A∂B​ΔA+Bα​(8)

结合结合能的半经验公式：

B=avA−asA2/3−aa(A2−Z)2A−acZ2A1/3+BpB = a_vA - a_sA^{2/3} -a_a \frac{(\frac{A}{2}-Z)^2}{A} - a_c\frac{Z^2}{A^{1/3}} + B_p B=av​A−as​A2/3−aa​A(2A​−Z)2​−ac​A1/3Z2​+Bp​

其中对能的部分在子核与母核间的变化很小。

可以近似得到：

Ed=Bα−4av+8as31A1/3−aa(1−2ZA)2+4acZA1/3(1−Z3A)(9)\begin{aligned} E_d = & B_\alpha - 4a_v + \frac{8a_s}{3}\frac{1}{A^{1/3}} -a_a(1-\frac{2Z}{A})^2\\ & + 4a_c\frac{Z}{A^{1/3}} (1-\frac{Z}{3A})\tag{9} \end{aligned} Ed​=​Bα​−4av​+38as​​A1/31​−aa​(1−A2Z​)2+4ac​A1/3Z​(1−3AZ​)​(9)

带入各个参量的数值得到衰变能随质量数的变化关系，如下图。其中虚线为我们数值计算的结果，实线为测量值。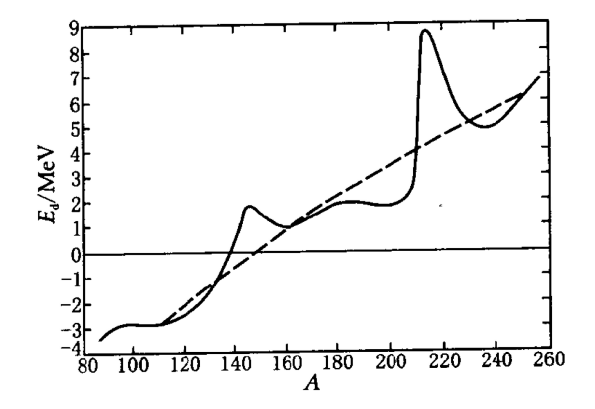

Fig：衰变能随质量数的变化[1]^{[1]}[1]

我们发现，利用原子核液滴模型得到的结合能半经验公式，我们能预测在 A>150A>150A>150 时，α\alphaα 衰变能大于零。这与实验结果基本一致。但是虚线不能反映变化的起伏现象。这一点需要使用核结构的壳模型。

衰变能随同位素的变化

实验发现，同一元素的各种同位素的 α\alphaα 衰变能可以近似连成一条直线。如下图所示：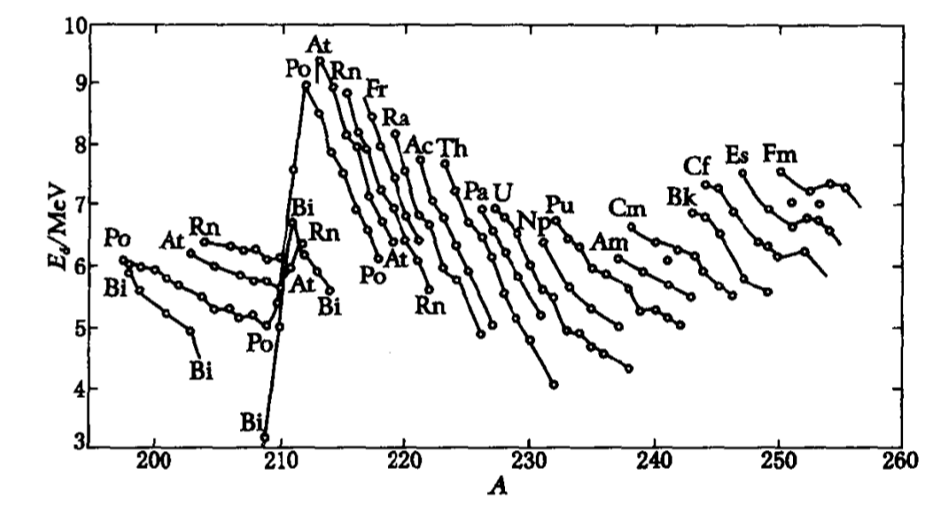

Fig：衰变能随同位素的变化

利用 (9)(9)(9) 可得：

∂Ed∂A=−16.29A4/3−371.20ZA2(1−2ZA)−0.952ZA4/3(1−4Z3A)\frac{\partial E_d}{\partial A} = - \frac{16.29}{A^{4/3}} - 371.20 \frac{Z}{A^2}(1-\frac{2Z}{A})-0.952\frac{Z}{A^{4/3}}(1-\frac{4Z}{3A}) ∂A∂Ed​​=−A4/316.29​−371.20A2Z​(1−A2Z​)−0.952A4/3Z​(1−3A4Z​)

不难得到，上述式子中每项都是负的，由此对应的斜率是负的。衰变能随着质量数增加而减小。实验发现，在一定的范围内（A=209∼213A=209\sim 213A=209∼213）的范围内，对于 Bi,Po,At,Rn\mathrm{Bi},\mathrm{Po},\mathrm{At},\mathrm{Rn}Bi,Po,At,Rn 等同位素的规律与预言的相反，这说明了液滴模型的局限性。

衰变能和衰变常量的关系

1911年，盖格（Geiger）和努塔尔（Nuttall）总结得到了如下经验定律（盖格-努塔尔定律）：

λ=aR57.5(10)\lambda = aR^{57.5} \tag{10} λ=aR57.5(10)

其中：

其中射程与能量有如下经验关系：

R∝E3/2(11)R \propto E^{3/2} \tag{11} R∝E3/2(11)

于是 (10)(10)(10) 可改写为：

λ=a′E86.25(12)\lambda = a' E^{86.25} \tag{12} λ=a′E86.25(12)

需要指出，由于实验水平的受限，盖格-努塔尔定律具有很大的近似性。但是其可以反映衰变常量 λ\lambdaλ 随着衰变能 EdE_dEd​ 剧烈改变的趋势。

现在考虑 α\alphaα 粒子是如何从原子核中发射出来的。

假设原子核内存在高速运动的 α\alphaα 粒子。核内的 α\alphaα 粒子与其他核子之间主要存在两种相互作用力：核力与库仑力。核力是短程力，在原子核内，α\alphaα 粒子的运动是渐近自由的。在原子核外，核力几乎为零，此时考虑库仑力。α\alphaα 粒子相对于子核的势能可以写为：

V(r)={−V0rR(13)V(r) = \left\{ \begin{aligned} &-V_0\quad &rR\\ \end{aligned} \right.\tag{13} V(r)=⎩⎪⎨⎪⎧​​−V0​4πε0​r2(Z−2)e2​​rR​(13)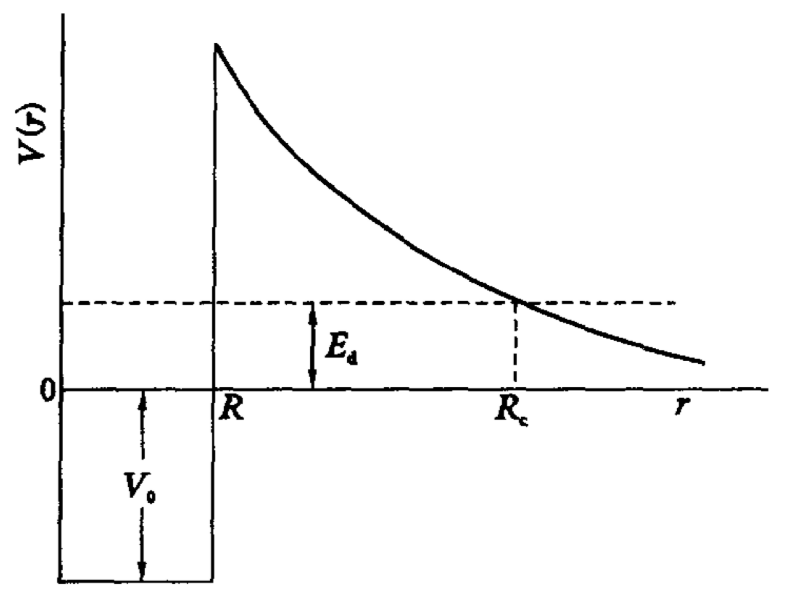

Fig：α\alphaα 衰变的势能曲线

RRR 为原子核边界。我们近似取：

R=(A11/3+A21/3)r0(14)R = (A_1^{1/3}+A_2^{1/3})r_0 \tag{14} R=(A11/3​+A21/3​)r0​(14)

其中 r0≈1.45fmr_0\approx 1.45\mathrm{fm}r0​≈1.45fm。

我们以上采用的势能忽略在 RRR 处变化的细节，但对讨论的问题影响不大。

α\alphaα 粒子的能量一般在 4∼9MeV4\sim 9\mathrm{MeV}4∼9MeV，但是得到的库伦势垒却比 α\alphaα 衰变能高得多（例如计算得到 84212Po\mathrm{^{212}_{84}Po}84212​Po）的 α\alphaα 的库伦势垒能量为 22MeV22\mathrm{MeV}22MeV。经典理论不能理解 α\alphaα 粒子为何能跨过如此高的势垒到原子核以外。这反映了经典力学的局限性。

在量子力学中，微观粒子是有一定的概率穿过势垒的，这就是 隧穿效应。

由 WKB\mathrm{WKB}WKB 近似可以得到粒子穿过势垒的概率：

P=e−G=exp⁡{−2ℏ∫R1R2[2μ(Z1Z2e24πε0r−Ed)]1/2dr}(15)\begin{aligned} P &= e^{-G}\\ & = \exp\{-\frac{2}{\hbar}\int_{R_1}^{R_2}[2\mu(\frac{Z_1Z_2e^2}{4\pi\varepsilon_0r} - E_d)]^{1/2} dr\}\\ \end{aligned}\tag{15} P​=e−G=exp{−ℏ2​∫R1​R2​​[2μ(4πε0​rZ1​Z2​e2​−Ed​)]1/2dr}​(15)

式中 μ\muμ 为折合质量，EdE_dEd​ 可用 RcR_cRc​ 表示：

Ed=Z1Z2e24πε0Rc(16)E_d = \frac{Z_1Z_2e^2}{4\pi\varepsilon_0R_c}\tag{16} Ed​=4πε0​Rc​Z1​Z2​e2​(16)

代入 (15)(15)(15)，得到：

G=22μEdℏ∫RRc(Rcr−1)1/2dr=2Rc2μEdℏ[x(R)−12sin⁡2x(R)](17)\begin{aligned} G &= \frac{2\sqrt{2\mu E_d}}{\hbar}\int_{R}^{R_c}(\frac{R_c}{r}-1)^{1/2}dr \\ &= \frac{2R_c\sqrt{2\mu E_d}}{\hbar}[x(R)-\frac{1}{2}\sin 2x(R)]\\ \end{aligned}\tag{17} G​=ℏ22μEd​​​∫RRc​​(rRc​​−1)1/2dr=ℏ2Rc​2μEd​​​[x(R)−21​sin2x(R)]​(17)

其中 xxx 为以下函数

x(r)=arccos⁡(rRc)1/2x(r) = \arccos(\frac{r}{R_c})^{1/2} x(r)=arccos(Rc​r​)1/2

不妨考虑

ψ(RRc)=x(R)−12sin⁡2x(R)=arccos⁡(RRc)1/2−(RRc−R2Rc2)1/2(18)\begin{aligned} \psi(\frac{R}{R_c}) &= x(R)-\frac{1}{2}\sin 2x(R)\\ &=\arccos(\frac{R}{R_c})^{1/2}-(\frac{R}{R_c}-\frac{R^2}{R_c^2})^{1/2}\\ \end{aligned}\tag{18} ψ(Rc​R​)​=x(R)−21​sin2x(R)=arccos(Rc​R​)1/2−(Rc​R​−Rc2​R2​)1/2​(18)

通常来说：R/RcR/R_cR/Rc​ 小于 13\frac{1}{3}31​，因此考虑取 (18)(18)(18) 式的一阶近似：

ψ(RRc)≈π2−2(RRc)1/2(19)\psi(\frac{R}{R_c}) \approx \frac{\pi}{2} - 2(\frac{R}{R_c})^{1/2} \tag{19} ψ(Rc​R​)≈2π​−2(Rc​R​)1/2(19)

因此 (17)(17)(17) 式成为：

G=2Rc2μEdℏ[π2−2(RRc)1/2]=2μ(Z−2)e22ε0ℏEd−4e[μ(Z−2)R]1/2πε0ℏ(20)\begin{aligned} G &= \frac{2R_c\sqrt{2\mu E_d}}{\hbar}[\frac{\pi}{2}-2(\frac{R}{R_c})^{1/2} ]\\ &=\frac{\sqrt{2\mu}(Z-2)e^2}{2\varepsilon_0\hbar\sqrt{E_d}} - \frac{4e[\mu(Z-2)R]^{1/2}}{\sqrt{\pi\varepsilon_0}\hbar}\\ \end{aligned}\tag{20} G​=ℏ2Rc​2μEd​​​[2π​−2(Rc​R​)1/2]=2ε0​ℏEd​​2μ​(Z−2)e2​−πε0​​ℏ4e[μ(Z−2)R]1/2​​(20)

于是 α\alphaα 粒子穿透势垒的概率为：

P=exp⁡{−2μ(Z−2)e22ε0ℏEd+4e[μ(Z−2)R]1/2πε0ℏ}(21)P = \exp\{-\frac{\sqrt{2\mu}(Z-2)e^2}{2\varepsilon_0\hbar\sqrt{E_d}} + \frac{4e[\mu(Z-2)R]^{1/2}}{\sqrt{\pi\varepsilon_0}\hbar}\}\tag{21} P=exp{−2ε0​ℏEd​​2μ​(Z−2)e2​+πε0​​ℏ4e[μ(Z−2)R]1/2​}(21)

λ\lambdaλ 是单位时间内发生 α\alphaα 衰变的概率，它应该等于 α\alphaα 粒子在单位时间内碰撞势垒的次数 nnn 与穿透概率 PPP 的乘积。我们简单地考虑 α\alphaα 在半径为 R′R'R′ 的母核内以 vvv 的速度运动，那么有：

n=v2R′(22)n = \frac{v}{2R'} \tag{22} n=2R′v​(22)

对应的，可以将衰变常量写为：

λ=nP=v2R′exp⁡{−2μ(Z−2)e22ε0ℏEd+4e[μ(Z−2)R]1/2πε0ℏ}(23)\begin{aligned} \lambda &= nP\\ &= \frac{v}{2R'}\exp\{-\frac{\sqrt{2\mu}(Z-2)e^2}{2\varepsilon_0\hbar\sqrt{E_d}} + \frac{4e[\mu(Z-2)R]^{1/2}}{\sqrt{\pi\varepsilon_0}\hbar}\}\\ \end{aligned}\tag{23} λ​=nP=2R′v​exp{−2ε0​ℏEd​​2μ​(Z−2)e2​+πε0​​ℏ4e[μ(Z−2)R]1/2​}​(23)

我们发现，λ\lambdaλ 可写做如下形式：

ln⁡λ=A−BEd−1/2(24)\ln \lambda = A - B E_d^{-1/2} \tag{24} lnλ=A−BEd−1/2​(24)

这可以解释，为什么随着衰变能的变化，衰变常量变化巨大。另外，我们发现 λ\lambdaλ 是依赖于 RRR 的，我们可以利用这一点通过测量衰变常量来确定衰变能量。

(23)(23)(23) 式在定量解释偶偶核的 α\alphaα 衰变是成功的。但是对于奇奇核，理论与实验出现了严重分歧。通常引入禁戒因子来描述实验半衰期 TexpT_{exp}Texp​ 与理论半衰期 TthT_{th}Tth​ 之间的差别：

F=TexpTth(25)F = \frac{T_{exp}}{T_{th}}\tag{25} F=Tth​Texp​​(25)

一般来说，对于奇奇核，禁戒因子在 100∼1000100\sim 1000100∼1000（也有高达 101410^{14}1014），可能有以下原因导致了实验与理论的分歧：

角动量的影响

离心势能的影响，导致 α\alphaα 粒子更难穿透势垒。

形成因子的影响

之前初始假设在核内存在 α\alphaα 粒子，实际情况 α\alphaα 粒子可能是在衰变过程中产生的。