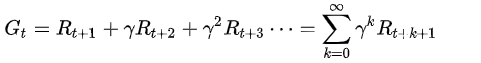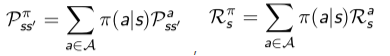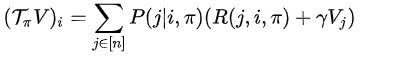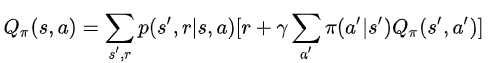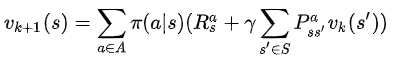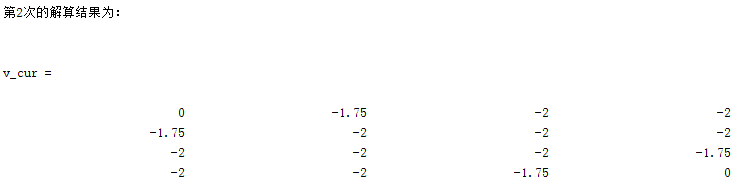运筹优化学习18：马尔科夫决策过程与动态规划 (手算及Matlab源码剖析)

您所在的位置：网站首页 › 动态规划是算法还是模型的 › 运筹优化学习18：马尔科夫决策过程与动态规划 (手算及Matlab源码剖析)

运筹优化学习18：马尔科夫决策过程与动态规划 (手算及Matlab源码剖析)

2024-07-04 18:55| 来源: 网络整理| 查看: 265

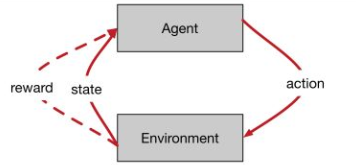
1 基本概念

2 马尔科夫决策过程理论

2.1 马尔科夫过程(Markov process / Markov Chain)

2.1.1 状态空间分析：

2.1.2 转移矩阵描述

2.2 马尔科夫奖励过程(Markov Reward Process)

2.2.1 不同任务的奖励及回报值计算方法

2.2.2 衰减因子的分析

2.2.3 马尔科夫奖励过程的值函数及计算示例

2.3 马尔科夫决策过程(Marlov Decision Process)

2.3.1 策略

2.3.2 状态价值函数与状态动作价值函数

3 动态规划算法求解MDP

3.1 预测与控制

3.2 求解算法梳理

4 值迭代与策略迭代手算及Matlab代码

4.1 简单粗暴的值迭代方法--求解Small Gridworld例子

4.1.1 理论部分

4.1.1 手解过程及自己总结

4.1.2 Matlab的计算结果实现

4.1.3 Matlab部分解算结果展示：

4.2 策略迭代算法

4.2.1 手算示例分析

4.2.2 策略迭代的Matlab实现

4.2.3 运行结果展示

参考资料：

写在前面的话

本文为笔者自学马尔科夫过程的新的总结，难免存在疏漏和错误之处；写作本文的目的是为想学习马尔科夫决策过程的小伙伴提供一些参考本文的撰写也借鉴了许多优秀的知乎及CSDN博客文章，感谢他们，但是本文在借鉴他们成果的基础上，做了自己的一些改编，不合适之处，欢迎高人批评指正。由于本人也是初学，旨在对问题概念及原理做最为直白的理解，确保初学者无痛入门如后期自己发现有疏漏之处，也会自行不断地进行更新和完善 1 基本概念

在无监督数据、只有奖励信号；奖励可能是即时的也可能是延迟的；当前行为影响后续状态的收益；时间是一个必须要考虑的因素。强化学习是通过个体与环境的不断交互和反馈积累起对环境的感知，进而一步步的增强自己对环境的认识而尽快的实现自己的目的

$R_{t}$ 表示个体在 t 时刻的奖励，强化学习的目标就是获得最大化的奖励

序列决策：通过一系列的行为得到决策收益，有时候会放弃短期利益追求长期效益个体(agent)：行动的实际实施者，用于接收信号并做出决定。个体在环境状态 $S_{t}$ 采用动作 $A_{t}$ 得到收益 $R_{t+1}$ 环境(Environment)：接收一个动作 $A_{t}$ ，环境状态变成 $S_{t+1}$ ，反馈给个体一个收益 $R_{t+1}$ 行动(action)：个体施加在行动中的动作状态(state)：环境接受个体agent的action后，反馈给agent的环境状态，同时还会附加一个奖励reward

历史：状态、动作和收益的序列马尔科夫性： $P(S_{t+1}|S_{t})=P(S_{t+1}|S_{t},S_{t-1}, ..., S_{1})$ ,忽略历史信息，当前状态可以决定未来策略：状态到行为的映射价值函数：未来奖励的预测，评价当前状态的好坏。当个体面临几种不同的状态时，他会根据value值来评估不同状态的收益情况，指定相应的策略；也就是说，价值函数是基于某一策略而言的。对于某一策略 $\pi$ ,其价值函数可表示为 $v_{\pi}(s)=E_{\pi}(R_{t+1}+\gamma R_{t+2}+\gamma^{3} R_{t+3}+... | s_{t}=s )$ 模型：对模拟环境与个体交互机制的描述，模型包含两个部分：状态之间的转移概率 $P_{ss'}^{a}=P[{S_{t+1} | S_{t}=s,S_{t+1}=s',A_{t}=a}]$ 状态转移的收益 $R_{s}^{a}=E(R_{t+1} | S_{t}=s, A_{t} = a)$ 注意：模型仅对于个体来说的，模型对个体来说也不是必须的；考虑环境的实际规划状态的研究称为环境动力学学习与规划：学习是在初始阶段对环境一无所知的时候，通过与环境的不断交互，建立起相应的行为策略；规划是在个体对环境已经了解后，利用建立的模型模拟与环境的交互，从而继续改进所建立的策略。探索和利用：个体从未知环境中找到一个比较好的策略，有失败的风险；利用则是从已有的策略中选择一个比较好的策略，或许会早熟。比如：你会选择一个新餐厅吃饭 (探索) 还是去你之前去过的餐厅 (利用) 呢？ 2 马尔科夫决策过程理论

马尔科夫过程基本描述：

马尔科夫性： $P(S_{t+1}|S_{t})=P(S_{t+1}|S_{t},S_{t-1}, ..., S_{1})$ 状态转移概率： $P_{ss'}^{a}=P[{S_{t+1} | S_{t}=s,S_{t+1}=s',A_{t}=a}]$ ；显然从在任意时刻 t 从当前状态转移到其他状态的概率之和为1 2.1 马尔科夫过程(Markov process / Markov Chain)

无记忆过程，包含两个基本要素：，其中的 S 表示有限个状态集合，P 表示这些状态之间的转移概率

马尔科夫链的基本示例

上图模拟了包含S= {Facebook, Class1, Class2, Class3, Pub, Pass,Sleep}七种状态的马尔科夫状态空间，其中圆形状态表示个体所处的状态，方形状态Sleep表示终止状态；不同状态之间的连线上的数值表示这些状态之间的转移概率，箭头表示状态转移的方向。

2.1.1 状态空间分析：个体从Class1开始，他有0.5的概率，转移到Class2；也有可能0.5的概率，转移到Facebook状态；当个体从状态Class1转移到状态Facebook时，他有0.9的概率，继续刷Facebook；也有0.1的概率回到Class;当个体从状态Class1转移到状态Class2时，他有0.2的概率会因课程太难退出，即Sleep；有0.8的概率，转到Class3；当个体从状态Class2转移到状态Class3时，他有0.6的概率通过考试，然后退出；有0.4的概率，去图书馆查资料学习；如果他去图书馆查资料学习，有0.4的概率返回Class1；有0.4的概率，返回Class2；有0.2的概率，返回Class1

思维导图展示：

学生上课马尔科夫过程思维导图演示 2.1.2 转移矩阵描述学生选课马尔科夫转移矩阵 Class1Class2Class3FacebookPubPassSleepClass1 0.5 0.5 Class2 0.8 0.2Class3 0.40.6 Pub0.20.40.4 Facebook0.9 0.1 Pass 1Sleep 1

上图和表解释了马尔科夫过程的两个基本要素：状态空间和状态转移矩阵，下面介绍马尔科夫奖励过程。

2.2 马尔科夫奖励过程(Markov Reward Process)

在马尔科夫过程的基础上，加入了奖励R；构成形如 $S,P,R,\gamma$ 的马尔科夫奖励过程；对其四元组的解释如下：

S：马尔科夫的状态空间P：马尔科夫的状态转移概率矩阵R：马尔科夫过程的奖励函数 $\gamma$ ：奖励衰减因子，位于[0, 1]之间；传达的信息是，随着状态的迁移，当前状态的影响在衰减 2.2.1 不同任务的奖励及回报值计算方法

注意：

我们将每个状态的即时收益，定义为奖励 $R_{t}$ ；而将对某一个片段的评价，定义为回报 $G_{t}$ ；短期的叫收益，长期的叫回报，区分开来，以免混淆

( 1 ) 回合制任务(episodic task)

存在一个终止状态，并且所有的奖励会在这个终止状态及其之前结算

( 2 ) 连续任务(continuing task)

不存在一个终止状态，即原则上可以永久地运行下去，这类任务的奖励是分散地分布在这个连续的一连串的时刻中的

其中衰减率（discount factor） $\gamma$ 满足 $0 \leq \gamma \leq 1$ 。这样的定义也很好理解，相比于更远的收益，我们会更加偏好临近的收益，因此对于离得较近的收益权重更高。

2.2.2 衰减因子 $\gamma$ 的分析

分析性描述：

我们对未来的把握是逐渐衰减的，一般的情况下，我们更关心短时间的奖励加入衰减因子之后，我们就可通过该参数来调节长时间的回报衰减因子是MDP和MRP长期回报值有界的保证 2.2.3 马尔科夫奖励过程的值函数及计算示例

$v(s) & = E(G_{t} | S_{t}=s) \\ &= E(R_{t+1} + \gamma R_{t+2} + \gamma^{2} R_{t+3} + ... | S_{t}=s) \\ &= E(R_{t+1} + \gamma * (R_{t+2} + \gamma R_{t+3} + ...) | S_{t}=s) \\ &= E(R_{t+1} + \gamma * v(S_{t+1})) | S_{t}=s)$

价值函数表示了状态s和状态 $S_{t+1}$ 之间的迭代关系，也反应了短期奖励与长期回报之间的关系

如果我们知道状态转移矩阵P，那么式子可转化为：

$v(s) & = R_{t+3} + ...) | S_{t}=s) \\ &= E(R_{t+1} + \gamma * v(S_{t+1})) | S_{t}=s) \\& = E(R_{t+1} | S_{t}=s) + \gamma * E(v(S_{t+1} | S_{t} = s)) \\& = R(s) + \gamma * \sum_{s' \in S} (P_{ss'} v(s'))$

下面是一个例子：

值函数的计算示例 2.3 马尔科夫决策过程(Marlov Decision Process)

在马尔科夫奖励过程的基础上，我们又加入了行动集合，构成 $S,A,P,R,\gamma$ 五元组和策略 $\pi$ 形式的马尔科夫决策过程

几点讨论：

MP和MRP我们作为一个观察者，观察状态的变化来计算回报值；而在MDP中，我们引入了决策，通过改变状态转移的流程，获得最大化的回报我们对MDP的奖励变成了对的奖励，即通过动作来控制状态的转移 2.3.1 策略策略给出了在每个状态下我们应该采取的行动，我们可以把这个策略记做 $\pi (a|s)$ ，它表示在状态 $s$ 下采取行动 $a$ 的概率给定状态下的动作概率的集合，这些所有的概率的加总起来，和值为1。策略是对agent行为的全部描述，一旦策略确定智能体的行为也将确定。策略是基于马尔科夫状态，是时间稳定的，只与状态有关，而与时间无关如果给定策略 $\pi$ ，MDP将会退化为MRP问题

当策略确定时，对应的是一组动作集合；当策略随机时，对应的是一组动作分布集合

如果我们可以计算出每个状态或者采取某个行动之后收益，那么我们每次行动就只需要采取收益较大的行动或者采取能够到达收益较大状态的行动。这就是策略迭代的核心所在。

2.3.2 状态价值函数与状态动作价值函数

两个状态价值函数对应两个贝尔曼方程，对应值迭代和策略迭代算法，两个公式的用途不同，千万不能混淆。

(1) 状态价值函数( $V_{\pi}(s)$ ，state value function)

$v_{\pi}(s) \\ = E_{\pi}(G_{t} | S_{t} = s) \\ = E_{\pi}(R_{t+1} + \gamma * v_{\pi}(S_{t+1}) | S_{t} = s)$

在当前状态 $s$ 一直采用策略 $\pi$ ，能够产生的期望收益

个人观点：

如果你只给出一个策略，使用值迭代算法更新至值函数收敛，你将得到了这个策略下的最优决策，这样的计算模式只涉及到上式的前两行部分；因为只有一个策略，所有的 $\pi (a|s)$ 就是确定的。上面公式的通俗解释是，我在状态 s 处以概率 $\pi (a|s)$ 采取行动 a，采取行动 a 之后，状态 s 能够以概率 $p(s',r | s,a)$ 转移到状态 s' 。对于策略 $\pi$ ，我们可以定义如下贝尔曼方程：

(2) 状态动作价值函数（ $Q_{\pi}(s,a)$ , action value function）

$q_{\pi}(s,a) \\ = E_{\pi}(G_{t} | S_{t} = s, A_{t}=a) \\ = E_{\pi}(R_{t+1} + \gamma * q_{\pi}(S_{t+1},A_{t+1}) | S_{t} = s, A_{t}=a)$

当前状态 $s$ ，如果采用行动 $a$ ，接下来采用策略 $\pi$ ，能够产生的期望收益

如果我们我们能够求得某策略下的价值函数，我们就可以对该策略进行评估如果我们能够得到最优状态的价值函数，我们就可以得到最优策略

(3) 状态值函数与状态动作值函数区别与联系分析

状态价值函数，策略是确定的；而状态动作价值函数，采取某个行动之后，选择不同的策略能够得到的预期收益状态价值函数，对应于值迭代算法；行动价值函数，对应策略迭代算法

联系：

两个函数的最终目的都是要得到最优的期望收益，用【殊途同归】一词描述最为合适

一个计算的示例

$\upsilon\left(s_4\right)=0.5*\left(1+0.2*\left(-1.3\right)+0.4*2.7+0.4*7.4\right)+0.5*10=7.39$

3 动态规划算法求解MDP

动态表示研究的过程是具有时序特征，规划是一种优化策略；所以动态规划是指将研究问题分解成许多个子问题，通过不断的求解子问题一步一步递归得到原问题的解决方案。

对于我们研究的马尔科夫过程，由于贝尔曼方程的存在，使其具备使用动态规划求解的基本特征；不过要想使用动态规划来求解MDP的话，MDP必须具有明确的模型，事先知道完全的信息。【根据状态和行动的价值函数，计算每个状态的最优策略，最后串起来】

3.1 预测与控制预测是求解给定策略下的价值函数的过程控制是找到一个策略以获得最大化的收益，即从所有的可能策略中选择最优的价值函数和最优策略

MDP的动态规划算法的主体思路为：先给一个策略，预测出他的最优值函数；然后在使用控制策略，得到最优策略

策略迭代方法：要进行策略迭代，首先要进行策略评估，也就是评估一下目前的几个选择的好坏，因为只有你当前的选择好了，你才更可能做出整体上比较好的选择；在DS的视频中，提出了“one step look ahead”理念，就是说我计算当前值函数的时候，要使用到上一个值函数的数据来构建；

3.2 求解算法梳理

(1) 策略评估

概念：评估一个给定的策略，属于预测的范畴

计算公式：

说明：一次迭代内，状态s的价值等于前一次迭代该状态的即时奖励与所有s的下一个可能状态s' 的价值与其概率乘积的和

(2) 策略改善

采取那个（些）使得状态价值得到最大的行为，进行策略更新。

考虑一个确定的策略： $a=\pi_{s}$ 通过贪婪计算优化策略： $\pi'(s) = argmax_{a \in A}q_{\pi}(s|a)$ 这会用1步迭代改善状态s的q值，即在当前策略下，状态s在动作π’(s)下得到的q值等于当前策略下状态s所有可能动作得到的q值中的最大值。这个值一般不小于使用当前策略得到的行为所的得出的q值，因而也就是该状态的状态价值。如果q值不再改善，则在某一状态下，遵循当前策略采取的行为得到的q值将会是最优策略下所能得到的最大q值，上述表示就满足了Bellman最优方程，说明当前策略下的状态价值就是最优状态价值。因而此时的策略就是最优策略。

(3) 策略迭代

在当前策略上迭代计算 v 值，再根据 v 值贪婪地更新策略，如此反复多次，最终得到最优策略 $\pi^{*}$ 和最优状态价值函数 $V^{*}$

策略迭代算法流程示意图

(4) 价值迭代

概念：从初始状态价值开始同步迭代计算，最终收敛，整个过程中没有遵循任何策略。

公式定理：

说明：与策略迭代不同，在值迭代过程中，算法不会给出明确的策略，迭代过程其间得到的价值函数，不对应任何策略；价值迭代虽然不需要策略参与，但仍然需要知道状态之间的转移概率，也就是需要知道模型。

4 值迭代与策略迭代手算及Matlab代码 4.1 简单粗暴的值迭代方法--求解Small Gridworld例子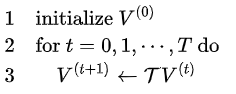

值迭代算法流程图 4.1.1 理论部分

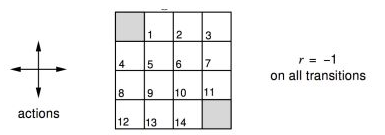
一个4×4的小网格世界，左上角和右下角是目的地

每个格子行动方向为上下左右，每走一步reward-1

求一个在每个状态都能以最少步数到达目的地的最优行动策略。

解决思路：我们从最开始的随机（1/4）策略开始，对其进行policy evaluation, 然后进行policy iteration by acting greedy

4.1.1 手解过程及自己总结

展示k=2到k=3的计算过程：

0 = 【第一行第一个格子】

这是结束的位置，应该保持不动

-2.375 =

【第一行的第二个格子】 + 0.25 * (-1 + 1 * (-1.7))

上【-0.675】 + 0.25 * (-1 + 1 * (0))

左【-0.25】 + 0.25 * (-1 + 1 * (-2))

下【-0.75】 + 0.25 * (-1 + 1 * (-2))

右【-0.75】

-2.875 =

【第一行的第三个格子】 + 0.25 * (-1 + 1 * (-2))

上【-0.75】 + 0.25 * (-1 + 1 * (-1.7))

左【-0.625】 + 0.25 * (-1 + 1 * (-2))

下【-0.75】 + 0.25 * (-1 + 1 * (-2))

右【-0.75】

-3.0 =

【第一行的第四个格子】 + 0.25 * (-1 + 1 * (-2))

上【-0.75】 + 0.25 * (-1 + 1 * (-2))

左【-0.75】 + 0.25 * (-1 + 1 * (-2))

下【-0.75】 + 0.25 * (-1 + 1 * (-2))

右【-0.75】

-2.425 =

【第二行第一列】 + 0.25 * (-1 + 1 * (0))

上【-0】 + 0.25 * (-1 + 1 * (-1.7))

左【-0.625】 + 0.25 * (-1 + 1 * (-2))

下【-0.75】 + 0.25 * (-1 + 1 * (-2))

右【-0.75】

-2.75 =【第二行第二列】 + 0.25 * (-1 + 1 * (-1.7)) 上【-0.625】 + 0.25 * (-1 + 1 * (-1.7)) 左【-0.625】 + 0.25 * (-1 + 1 * (-2)) 下【-0.75】 + 0.25 * (-1 + 1 * (-2)) 右【-0.75】-3.0 = 【第二行第三列】 + 0.25 * (-1 + 1 * (-2)) 上【-0.75】 + 0.25 * (-1 + 1 * (-2)) 左【-0.75】 + 0.25 * (-1 + 1 * (-2)) 下【-0.75】 + 0.25 * (-1 + 1 * (-2)) 右【-0.75】-2.875 = 【第二行第四列】 + 0.25 * (-1 + 1 * (-2)) 上【-0.75】 + 0.25 * (-1 + 1 * (-2)) 左【-0.75】 + 0.25 * (-1 + 1 * (-1.7)) 下【-0.625】 + 0.25 * (-1 + 1 * (-2)) 右【-0.75】-2.875 =【第三行第一列】 + 0.25 * (-1 + 1 * (-1.7)) 上【-0.625】 + 0.25 * (-1 + 1 * (-2)) 左【-0.75】 + 0.25 * (-1 + 1 * (-2)) 下【-0.75】 + 0.25 * (-1 + 1 * (-2)) 右【-0.75】-3.0 =【第三行第二列】 + 0.25 * (-1 + 1 * (-2)) 上【-0.75】 + 0.25 * (-1 + 1 * (-2)) 左【-0.75】 + 0.25 * (-1 + 1 * (-2)) 下【-0.75】 + 0.25 * (-1 + 1 * (-2)) 右【-0.75】-2.75 = 【第三行第三列】 + 0.25 * (-1 + 1 * (-2)) 上【-0.75】 + 0.25 * (-1 + 1 * (-2)) 左【-0.75】 + 0.25 * (-1 + 1 * (-1.7)) 下【-0.625】 + 0.25 * (-1 + 1 * (-1.7)) 右【-0.625】-2.375 = 【第三行第四列】 + 0.25 * (-1 + 1 * (-2)) 上【-0.75】 + 0.25 * (-1 + 1 * (-2)) 左【-0.75】 + 0.25 * (-1 + 1 * (-0)) 下【-0.25】 + 0.25 * (-1 + 1 * (-1.7)) 右【-0.625】-3.0 =【第四行第一列】 + 0.25 * (-1 + 1 * (-2)) 上【-0.625】 + 0.25 * (-1 + 1 * (-2)) 左【-0.75】 + 0.25 * (-1 + 1 * (-2)) 下【-0.75】 + 0.25 * (-1 + 1 * (-2)) 右【-0.75】-2.875 =【第四行第二列】 + 0.25 * (-1 + 1 * (-2)) 上【-0.75】 + 0.25 * (-1 + 1 * (-2)) 左【-0.75】 + 0.25 * (-1 + 1 * (-2)) 下【-0.75】 + 0.25 * (-1 + 1 * (-1.7)) 右【-0.625】-2.375 = 【第四行第三列】 + 0.25 * (-1 + 1 * (-2)) 上【-0.75】 + 0.25 * (-1 + 1 * (-2)) 左【-0.75】 + 0.25 * (-1 + 1 * (-1.7)) 下【-0.625】 + 0.25 * (-1 + 1 * (0)) 右【-0.25】-0 = 【第四行第四列】

通用的总结(k+1步的计算是从k步的值矩阵中取值来计算)：

某个格子的值 = 0.25 * (即时奖励[-1] + 折扣因子[1] * k步矩阵上方的值) 【上】 + 0.25 * (即时奖励[-1] + 折扣因子[1] * k步矩阵左方的值) 【左】 + 0.25 * (即时奖励[-1] + 折扣因子[1] * k步矩阵下方的值) 【下】 + 0.25 * (即时奖励[-1] + 折扣因子[1] * k步矩阵右方的值) 【右】

4.1.2 Matlab的计算结果实现

程序设计思路为：

构建gridRow * gridCol大小的图形初始化值函数，并定义当前值函数和上一步值函数；初始化折扣因子、即时奖励、终止阈值、策略概率按照前一部分总结的规律，依照【上->左->下->右】的顺序，迭代更新值函数；注：程序将边界点和内点分开计算判断更新后的值函数与上一步的值函数是否满足终止阈值；若是返回，得到收敛的值函数；否则继续迭代 clc;clear; %初始化格网的行数 girdRow = 4; gridCol = 4; %初始化值函数、当前值函数和上一期值函数 v = zeros(girdRow,gridCol); v_cur = v; v_before = v; %折扣因子 gamma = 1; %即时奖励 reward = -1; %策略概率 policyPossibility = 0.25; %终止阈值：两次的值函数差值小于给定阈值，认为得到了最优的值函数 theta = 0.00001; %迭代变量 iter = 0; while true %迭代变量递增1 iter = iter + 1; %遍历所有的格子 for i = 1:girdRow for j = 1:gridCol %第一行的第一个格子 if(i == 1 && j == 1) v_cur(i,j) = v_before(i,j); end %第一行其他格子 if(i == 1 && j ~= 1) if (j ~= gridCol) %上左下右 v_cur(i,j) = policyPossibility * (reward + gamma * v_before(i,j)) ... + policyPossibility * (reward + gamma * v_before(i,j-1)) ... + policyPossibility * (reward + gamma * v_before(i+1,j)) ... + policyPossibility * (reward + gamma * v_before(i, j+1)); else v_cur(i,j) = policyPossibility * (reward + gamma * v_before(i,j)) ... + policyPossibility * (reward + gamma * v_before(i,j-1)) ... + policyPossibility * (reward + gamma * v_before(i+1,j)) ... + policyPossibility * (reward + gamma * v_before(i, j)); end end %第1列其他格子 if (j == 1 && i ~= 1) if (i ~= girdRow) v_cur(i,j) = policyPossibility * (reward + gamma * v_before(i-1,j)) ... + policyPossibility * (reward + gamma * v_before(i,j)) ... + policyPossibility * (reward + gamma * v_before(i+1,j)) ... + policyPossibility * (reward + gamma * v_before(i, j+1)); else v_cur(i,j) = policyPossibility * (reward + gamma * v_before(i-1,j)) ... + policyPossibility * (reward + gamma * v_before(i,j)) ... + policyPossibility * (reward + gamma * v_before(i,j)) ... + policyPossibility * (reward + gamma * v_before(i,j+1)); end end %第4列非首行格子 if (j == gridCol && i ~= 1) if (i ~= gridCol) v_cur(i,j) = policyPossibility * (reward + gamma * v_before(i-1,j)) ... + policyPossibility * (reward + gamma * v_before(i,j-1)) ... + policyPossibility * (reward + gamma * v_before(i+1,j)) ... + policyPossibility * (reward + gamma * v_before(i, j)); else v_cur(i,j) = 0; end end %第4行非首列格子 if (i == girdRow && j ~= 1 && j ~= gridCol) v_cur(i,j) = policyPossibility * (reward + gamma * v_before(i-1,j)) ... + policyPossibility * (reward + gamma * v_before(i,j-1)) ... + policyPossibility * (reward + gamma * v_before(i,j)) ... + policyPossibility * (reward + gamma * v_before(i, j+1)); end %非边界行的计算 if (i~= 1 && i ~= girdRow && j ~= gridCol && j ~= 1) v_cur(i,j) = policyPossibility * (reward + gamma * v_before(i-1,j)) ... + policyPossibility * (reward + gamma * v_before(i,j-1)) ... + policyPossibility * (reward + gamma * v_before(i+1,j)) ... + policyPossibility * (reward + gamma * v_before(i, j+1)); end end end disp(sprintf('第%d次的解算结果为：',iter)) v_cur %输出当前值函数 if (max(abs(v_cur(:)-v_before(:))) < theta) break; else v_before = v_cur; end end 4.1.3 Matlab部分解算结果展示：

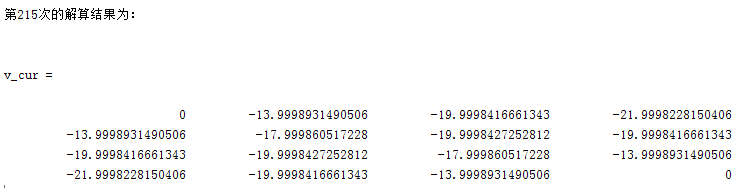
算法在设定的阈值内迭代了215次，最终输出的收敛结果为：

4.2 策略迭代算法

即使我们得到最优的值函数，我们还需要将其转化为具体的策略，而通过上面的例子我们的发现k=3与k=10的值函数不同，但对应的策略是完全相同的。故可以说我们仅需要迭代三次就得到了最优的策略，我们后面做的工作其实是无用功。

详细分析我们的值迭代的思路，发现我们自始至终沿用的都是均匀概率分布的策略；如果我们能在搜索的过程中根据值函数来更新策略，我们将有可能更快的得到想要的结果。正是基于这样的想法，我们的策略迭代算法就产生，其原理是这样的【自己悟的，专业人士勿喷】：

首先我们随机初始化一个策略，我们沿着这个策略进行值函数迭代，如果值函数发生变化，说明还没有得到最优的值函数，需要继续迭代，此时我们并不是直接对得到的值函数进行操作，而是根据值函数反应的信息，进行策略更新然后，使用更新后的策略，进行值函数的更新；如此往复，直到我们的值函数收敛或策略不再发生变化时，我们研究问题的满意解，甚至是最优解。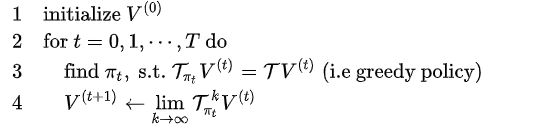

策略迭代流程图

插播别人的一段分析：伪代码的第3行表示策略改进，即固定价值函数，得到其最优策略；伪代码第4行的策略评估，即固定策略，得到其价值函数。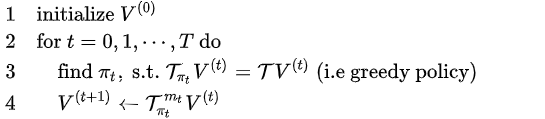

改进策略迭代流程图

改进策略迭代的分析：

当 $m_{t}=1$ 时，相当于只有一个策略，改进策略迭代算法等同于值迭代算法。结合策略评估的定义，我们仅在一个固定策略下，得到了其价值函数，也就是我们只做了一次策略评估。当 $m_{t}=\infty$ 时，改进策略迭代算法等同于策略迭代算法。改进策略迭代是值迭代算法与策略迭代算法的统一，目的都是为了找到最优的行动策略 4.2.1 手算示例分析

专业的公式我也看不懂，搞不明白，自己就发挥一下我的笨蛋大脑，写下下面这个部分，如有错误，欢迎指正。

再来分析之前出现的这个图，经过k=1的迭代，发现了新的策略：

比如第2行第1列的格子，其上左下右的值分别为-2.0、-2.0、-1.7、0.0，显然最大值函数对应方向为当前格子的上方；以第2行第2列的格子，其上左下右的值分别为-1.7、-1.7、-2.0、-2.0，出现了两个最大值，即上方和左方以第2行第3列的格子，其上左下右的值均为-2.0，出现了四个最大值

于是我就猜想，我们是不是可以做如下策略变换：

(row = 2,col = 1)处的策略，由 $\pi = \{0.25,0.25,0.25,0.25\}$ 变成 $\pi = \{1,0,0,0\}$ (row=2,col=2)处的策略，由 $\pi = \{0.25,0.25,0.25,0.25\}$ 变成 $\pi = \{0.5,0.5,0,0\}$ (row=2,col=3)处的策略，由 $\pi = \{0.25,0.25,0.25,0.25\}$ 保持不变

由此，对于k=2，我们得到新的策略集PI：

{0,0,0,0}{0,1,0,0}{0,1,0,0}{0.25,0.25,0.25,0.25}{1,0,0,0}{0.5,0.5,0,0}{0.25,0.25,0.25,0.25}{0,0,1,0}{1,0,0,0}{0.25,0.25,0.25,0.25}{0,0,0.5,0.5}{0,0,1,0}{0.25,0.25,0.25,0.25}{0,0,0,1}{0,0,0,1}{0,0,0,0}

基于更新后的策略，我们计算新的值函数，

-1

= 1 * ((-1) + 1 * (0))【左】

-2.7

= 1 * ((-1) + 1 * (-1.7))【左】

-3.0 = 0.25 * (-1 + 1 * (-2)) 【上】 + 0.25 * (-1 + 1 * (-2)) 【左】 + 0.25 * (-1 + 1 * (-2)) 【下】 + 0.25 * (-1 + 1 * (-2)) 【右】

-1

= 1 * ((-1) + 1 * (0))【上】

-2.7 = 0.5 * (-1 + 1 * (-1.7)) 【上】 + 0.5 * (-1 + 1 * (-1.7)) 【左】-3.0 = 0.25 * (-1 + 1 * (-2)) 【上】 + 0.25 * (-1 + 1 * (-2)) 【左】 + 0.25 * (-1 + 1 * (-2)) 【下】 + 0.25 * (-1 + 1 * (-2)) 【右】

-2.7

= 1 * (-1 + 1 * (-1.7))【下】

-2.7

= 1 * (-1 + 1 * (-1.7)）【上】

-3.0 = 0.25 * (-1 + 1 * (-2)) 【上】 + 0.25 * (-1 + 1 * (-2)) 【左】 + 0.25 * (-1 + 1 * (-2)) 【下】 + 0.25 * (-1 + 1 * (-2)) 【右】-2.7 = 0.5 * (-1 + 1 * (-1.7)) 【上】 + 0.5 * (-1 + 1 * (-1.7)) 【左】-1 = 1 * ((-1) + 1 * (0))【下】-3.0 = 0.25 * (-1 + 1 * (-2)) 【上】 + 0.25 * (-1 + 1 * (-2)) 【左】 + 0.25 * (-1 + 1 * (-2)) 【下】 + 0.25 * (-1 + 1 * (-2)) 【右】

-2.7

= 1 * ((-1) + 1 * (-1.7))【右】

-1

= 1 * ((-1) + 1 * (0))【右】

这样我们就得到了新的值函数，再由新的值函数进行策略更新，得到了下边的策略集：

{0,0,0,0}{0,1,0,0}{0,1,0,0}{0,0.5,0.5,0}{1,0,0,0}{0.5,0.5,0,0}{0.25,0.25,0.25,0.25}{0,0,1,0}{1,0,0,0}{0.25,0.25,0.25,0.25}{0,0,0.5,0.5}{0,0,1,0}{0.5,0,0,0.5}{0,0,0,1}{0,0,0,1}{0,0,0,0}

发现更新后的新策略居然跟之前的一样，是不是很神奇；这样我们就一路贪心的找到了最优策略。

这里还存在一个疑问，为啥在第2行第3列和第3行的第2列的策略不是四个方向呢？大神画的图，咱也不敢质疑，有高人可以解惑的不胜荣幸。

为什么要这么做能？我在想通过值函数我已经判断了某些方向的迭代预期是比较差的，我们就可以从中间选择那些好的让他去迭代呀；在我们的问题中，如果出现一个好的方向，我们以后就奔着这个好的方向去了；如果出现多个好的方向，我们也不知道那个方向更好，那就等概率的往这些方向去呗，反正走着走着，我们的美好生活就来了。

4.2.2 策略迭代的Matlab实现

基于上面的分析，我开发了Matlab程序，代码如下：

设计到三个函数：

函数名功能valueToPolicy根据值函数进行策略更新[使用负无穷-inf表示了跳出边界的行为]singleVI根据策略进行值函数更新getOptState给定某一状态的行为值函数，得到最优行为

状态最优行为更新

function policy = getOptState(actionVal) policy = zeros(length(actionVal),1); maxValue = max(actionVal); prob = 1 / sum(actionVal(:) == maxValue); for i = 1:length(actionVal) if(actionVal(i) == maxValue) policy(i) = prob; end end end

策略更新函数

%根据值函数更新策略 function policy = valueToPolicy(value) rowCnts = size(value,1); colCnts = size(value,2); tmpPolicyFlag = zeros(rowCnts * colCnts, 4); %定义极小数值M,将那些预跳出网络的操作设置为该值 M = -inf; for row = 1:rowCnts for col = 1:colCnts %第一行 if(row == 1) %第一行的第一个格子【上左下右】 if(col == 1) tmpPolicyFlag((row - 1) * colCnts + col,:) = getOptState([value(row, col), value(row, col), value(row+1, col), value(row, col+1)]); elseif(col < colCnts) tmpPolicyFlag((row - 1) * colCnts + col,:) = getOptState([M, value(row, col-1), value(row+1, col), value(row, col+1)]); else tmpPolicyFlag((row - 1) * colCnts + col,:) = getOptState([M, value(row, col-1), value(row+1, col), M]); end end %最后一个格子 if(col == colCnts && row == rowCnts) tmpPolicyFlag((row - 1) * colCnts + col,:) = getOptState([value(row-1, col), value(row, col-1), value(row, col), value(row, col)]); end %第一列非首行 if(col == 1 && row ~= 1) if(row ~= rowCnts) tmpPolicyFlag((row - 1) * colCnts + col,:) = getOptState([value(row-1, col), M, value(row+1, col), value(row, col+1)]); else tmpPolicyFlag((row - 1) * colCnts + col,:) = getOptState([value(row-1, col), M, M, value(row, col+1)]); end end %最后一列非尾行 if(col == colCnts && row ~= 1 && row ~= rowCnts) tmpPolicyFlag((row - 1) * colCnts + col,:) = getOptState([value(row-1, col), value(row, col-1), value(row+1, col), M]); end %最后一行掐头去尾 if(row == rowCnts && col ~= colCnts && col ~= 1) tmpPolicyFlag((row - 1) * colCnts + col,:) = getOptState([value(row-1, col), value(row, col-1), M, value(row, col+1)]); end %非边界行 if(row ~= rowCnts && row ~= 1 && col ~= colCnts && col ~= 1) tmpPolicyFlag((row - 1) * colCnts + col,:) = getOptState([value(row-1, col), value(row, col-1), value(row+1, col), value(row, col+1)]); end end %输出更新之后的策略 policy = tmpPolicyFlag; end

值函数更新

function [v_cur] = singleVI(v_before, policy, gamma, reward, gridRow, gridCol) v_cur = v_before; %遍历所有的格子 for i = 1:gridRow for j = 1:gridCol %第一行的第一个格子 if(i == 1 && j == 1) v_cur(i,j) = v_before(i,j); end %第一行其他格子 if(i == 1 && j ~= 1) if (j ~= gridCol) %上左下右 v_cur(i,j) = policy((i-1) * gridCol + j, 1) * (reward + gamma * v_before(i,j)) ... + policy((i-1) * gridCol + j,2) * (reward + gamma * v_before(i,j-1)) ... + policy((i-1) * gridCol + j,3) * (reward + gamma * v_before(i+1,j)) ... + policy((i-1) * gridCol + j,4) * (reward + gamma * v_before(i, j+1)); else v_cur(i,j) = policy((i-1) * gridCol + j,1) * (reward + gamma * v_before(i,j)) ... + policy((i-1) * gridCol + j,2) * (reward + gamma * v_before(i,j-1)) ... + policy((i-1) * gridCol + j,3) * (reward + gamma * v_before(i+1,j)) ... + policy((i-1) * gridCol + j,4) * (reward + gamma * v_before(i, j)); end end %第1列其他格子 if (j == 1 && i ~= 1) if (i ~= gridRow) v_cur(i,j) = policy((i-1) * gridCol + j,1) * (reward + gamma * v_before(i-1,j)) ... + policy((i-1) * gridCol + j,2) * (reward + gamma * v_before(i,j)) ... + policy((i-1) * gridCol + j,3) * (reward + gamma * v_before(i+1,j)) ... + policy((i-1) * gridCol + j,4) * (reward + gamma * v_before(i, j+1)); else v_cur(i,j) = policy((i-1) * gridCol + j,1) * (reward + gamma * v_before(i-1,j)) ... + policy((i-1) * gridCol + j,2) * (reward + gamma * v_before(i,j)) ... + policy((i-1) * gridCol + j,3) * (reward + gamma * v_before(i,j)) ... + policy((i-1) * gridCol + j,4) * (reward + gamma * v_before(i,j+1)); end end %第4列非首行格子 if (j == gridRow && i ~= 1) if (i ~= gridCol) v_cur(i,j) = policy((i-1) * gridCol + j,1) * (reward + gamma * v_before(i-1,j)) ... + policy((i-1) * gridCol + j,2) * (reward + gamma * v_before(i,j-1)) ... + policy((i-1) * gridCol + j,3) * (reward + gamma * v_before(i+1,j)) ... + policy((i-1) * gridCol + j,4) * (reward + gamma * v_before(i, j)); else v_cur(i,j) = 0; end end %第4行非首列格子 if (i == gridRow && j ~= 1 && j ~= gridCol) v_cur(i,j) = policy((i-1) * gridCol + j,1) * (reward + gamma * v_before(i-1,j)) ... + policy((i-1) * gridCol + j,2) * (reward + gamma * v_before(i,j-1)) ... + policy((i-1) * gridCol + j,3) * (reward + gamma * v_before(i,j)) ... + policy((i-1) * gridCol + j,4) * (reward + gamma * v_before(i, j+1)); end %非边界行的计算 if (i~= 1 && i ~= gridRow && j ~= gridCol && j ~= 1) v_cur(i,j) = policy((i-1) * gridCol + j,1) * (reward + gamma * v_before(i-1,j)) ... + policy((i-1) * gridCol + j,2) * (reward + gamma * v_before(i,j-1)) ... + policy((i-1) * gridCol + j,3) * (reward + gamma * v_before(i+1,j)) ... + policy((i-1) * gridCol + j,4) * (reward + gamma * v_before(i, j+1)); end end end end

主测试程序：值函数全部初始化为0，策略为各方向为0.25

clc;clear; %初始化格网的行数 gridRow = 4; gridCol = 4; %初始化值函数、当前值函数和上一期值函数 v = zeros(gridRow,gridCol); v_cur = v; v_before = v; %折扣因子 gamma = 1; %即时奖励 reward = -1; %定义1-2-3-4来表示行为方向,上左下右 action_direct = [1,2,3,4]; %定义初始策略 policy = [0.25,0.25,0.25,0.25; 0.25,0.25,0.25,0.25; 0.25,0.25,0.25,0.25; 0.25,0.25,0.25,0.25; 0.25,0.25,0.25,0.25; 0.25,0.25,0.25,0.25; 0.25,0.25,0.25,0.25; 0.25,0.25,0.25,0.25; 0.25,0.25,0.25,0.25; 0.25,0.25,0.25,0.25; 0.25,0.25,0.25,0.25; 0.25,0.25,0.25,0.25; 0.25,0.25,0.25,0.25; 0.25,0.25,0.25,0.25; 0.25,0.25,0.25,0.25; 0.25,0.25,0.25,0.25]; value = [0,0,0,0; 0,0,0,0; 0,0,0,0; 0,0,0,0]; %初始值和策略 oldValue = value; oldPolicy = policy; %最终值和策略 finalPolicy = policy; finalValue = value; %循环迭代 iter = 0; while(1) iter = iter + 1; newValue = singleVI(oldValue,oldPolicy,gamma, reward, gridRow,gridCol); newPolicy = valueToPolicy(newValue); if(newPolicy == oldPolicy) fprintf('第%d次的解算结果为：',iter) finalPolicy = newPolicy; finalValue = newValue; break; end oldPolicy = newPolicy; oldValue = newValue; end finalPolicy finalValue 4.2.3 运行结果展示

第3次的解算结果为： finalPolicy =

0.5 0.5 0 0 0 1 0 0 0 1 0 0 0 0.5 0.5 0 1 0 0 0 0.5 0.5 0 0 0.25 0.25 0.25 0.25 0 0 1 0 1 0 0 0 0.25 0.25 0.25 0.25 0 0 0.5 0.5 0 0 1 0 0.5 0 0 0.5 0 0 0 1 0 0 0 1 0 0 0.5 0.5

finalValue =

0 -1 -2 -3 -1 -2 -3 -2 -2 -3 -2 -1 -3 -2 -1 0

可知，进行了3次迭代我们边找了最优策略，终点的两个0.5可以忽略，我们按照其余非0元素所在的位置，按照上左下右的顺序，既可以解析出每个状态的最优行为策略。

参考资料：什么是动态规划（Dynamic Programming）？动态规划的意义是什么？《强化学习》第三讲动态规划寻找最优策略

强化学习(三)：动态规划求解MDP(Planning by Dynamic Programming)

一条咸鱼的强化学习之路3之策略迭代和价值迭代

强化学习基础篇: 策略迭代 (Policy Iteration)

【强化学习入门 1】从零开始认识强化学习

第一课：一文读懂马尔科夫过程

如果喜欢我的分享，可关注以下两个公众帐号

【本文地址】

运筹优化学习18：马尔科夫决策过程与动态规划 (手算及Matlab源码剖析)

运筹优化学习18：马尔科夫决策过程与动态规划 (手算及Matlab源码剖析)

今日新闻

推荐新闻