线性方程组的解 |
您所在的位置:网站首页 › 列主元消去法的优缺点 › 线性方程组的解 |
线性方程组的解
|
一、实验目的
(1)熟悉求解线性方程组的有关理论与方法。 (2)掌握Gauss列主元削去法和Gauss-Seidel迭代法的编程及应用。 (3)进一步了解两种算法的功能、优缺点,领会系数矩阵对解的影响。 二、实验内容用随机函数随机产生一个n阶线性方程组,用Gauss列主元削去法和Gauss-Seidel迭代法求解线性方程组,并且对该解进行验算及误差验证。 三、算法设计 3.1 列主元消去法
1.将输入的矩阵A和向量b转换为双精度浮点数类型。 2.通过循环进行高斯消元操作,将矩阵A化为上三角矩阵形式: 2.1每次迭代中,函数选取当前列的最大值作为主元,并将其所在的行与当前行交换。 2.2使用主元所在的行更新其他行的对应列元素,以消除当前列的其他元素。 3.使用回代法求解线性方程组: 从最后一行开始,依次计算每个未知数的值:对于第i行,使用已知的解x(i+1:end)和系数矩阵A的第i行来计算x(i)的值。 4.计算误差范围:通过计算矩阵A乘以解向量x与向量b之间的差的绝对值得到的。 5.将方程组、解和误差输出到图形窗口中。 3.2 Gauss-Seidel迭代法
2.然后,通过循环进行迭代计算: 2.1每次迭代中,函数使用高斯消元法更新解向量x的每个分量 2.2根据公式(b(i) - sum_ax) / A(i,i)更新解向量的第i个分量x_new(i)。 2.3判断是否满足终止条件: 如果新的解向量x_new与旧的解向量x之间的差值小于给定的误差阈值epsilon,则跳出循环。 否则,将新的解向量x_new赋值给旧的解向量x,继续下一次迭代。 3.最后,函数返回求解得到的解向量x。 4.计算误差范围:通过计算矩阵A乘以解向量x与向量b之间的差的绝对值得到 5.将方程组、解和误差输出到图形窗口中。 四、运行结果及分析调用上面两种迭代法,求解随机线性方程组的结果输出如下图所示:
图 9高斯赛德尔迭代法
图 10 列主元消去法 1.从上图可以看出,随机生成了线性方程组,这两种方法都能找到方程组的解,并且计算出误差,就是计算出的误差一直为0,不知道为什么,可能是精度原因。 2.高斯消元法:直接方法,通过消元和回代两个步骤解决线性方程组。这种方法的准确性高:它可以在有限步骤内找到线性方程组的精确解,但计算复杂度较高,对于大规模的线性方程组可能需要很长时间。 3.高斯-赛德尔迭代法:迭代方法,通过不断迭代改进解的估计值来求解线性方程组。这种方法对于稀疏矩阵,尤其是对于对角线占主导地位的矩阵,可以在较短的时间内找到近似解。但对其他的可能需要很多迭代才能找到足够精确的解,或者在某些情况下可能无法收敛。 五、小结通过本次实验,对这三种方程组求解算法的数学模型及基本算法原理和优缺特点有了更加深入的了解,并通过实践编码亲自实现,提高了编程能力。获益匪浅。 |
【本文地址】
今日新闻 |
推荐新闻 |


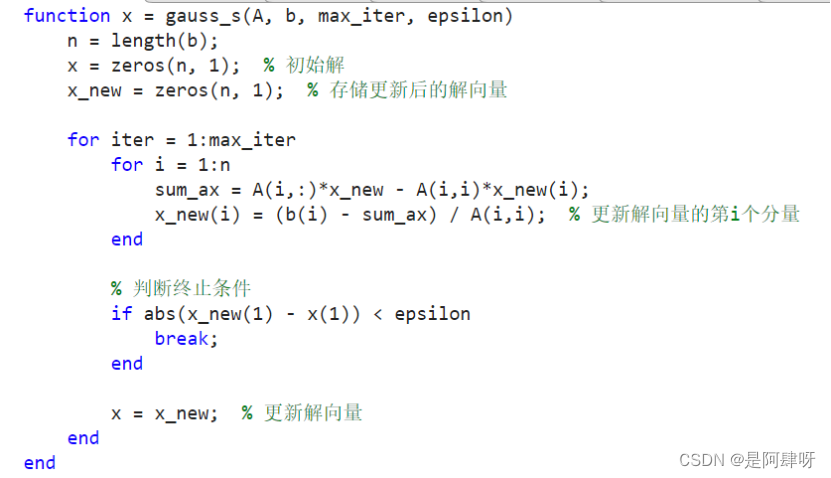 1.获取向量b的长度n,并初始化解向量x为全零向量。
1.获取向量b的长度n,并初始化解向量x为全零向量。
