【高等数学】多元函数 |
您所在的位置:网站首页 › 函数连续是函数可导的充分条件 › 【高等数学】多元函数 |
【高等数学】多元函数
|
多元函数-连续 偏导 可微
文章目录
多元函数-连续 偏导 可微定义1.连续定义2.偏导定义3.可微定义
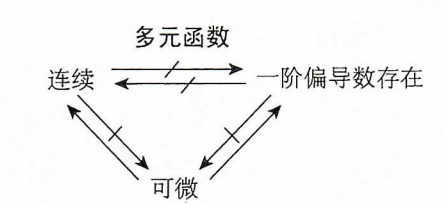
2.三者关系3.关系证明3.1 偏导和连续3.2 可微和偏导3.3 可微和连续
4.记忆方法5.参考文章
定义
1.连续定义
设二元函数 f ( P ) = f ( x , y ) f(P) = f(x,y) f(P)=f(x,y)的定义域为D, P 0 ( x 0 , y 0 ) P_0(x_0,y_0) P0(x0,y0)为D的聚点,且 P 0 ∈ D P_0 \in D P0∈D,若 l i m ( x , y ) → ( x 0 , y 0 ) f ( x , y ) = f ( x 0 , y 0 ) \displaystyle lim_{(x,y)\to(x_0,y_0)}f(x,y) = f(x_0,y_0) lim(x,y)→(x0,y0)f(x,y)=f(x0,y0) 则称函数 f ( x , y ) f(x,y) f(x,y)在 P 0 P_0 P0连续 聚点:如果给定任意的 δ > 0 \delta > 0 δ>0,点P的去心领域 U ( P , δ ) U(P,\delta) U(P,δ)内总有E的点,那么称P是E的聚点 2.偏导定义设函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)的某一领域内有定义,当 y y y固定在 y 0 y_0 y0,而x在 x 0 x_0 x0处有增量 Δ x \Delta x Δx时,相应的函数有增量 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) \displaystyle f(x_0+\Delta x,y_0) - f(x_0,y_0) f(x0+Δx,y0)−f(x0,y0) 如果 l i m Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x \displaystyle lim_{\Delta x \to 0} \frac{f(x_0+\Delta x,y_0) - f(x_0,y_0)}{\Delta x} limΔx→0Δxf(x0+Δx,y0)−f(x0,y0) 存在,那么称此极限为函数 z = f ( x , y ) z = f(x,y) z=f(x,y)在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)处对 x x x的偏导数,记作 ∂ z ∂ x ∣ x = x 0 , y = y 0 \displaystyle \frac{\partial z}{\partial x}|_{x=x_0,y=y_0} ∂x∂z∣x=x0,y=y0 , ∂ f ∂ x ∣ x = x 0 , y = y 0 \displaystyle \frac{\partial f}{\partial x}|_{x=x_0,y=y_0} ∂x∂f∣x=x0,y=y0, Z x ∂ x ∣ x = x 0 , y = y 0 \displaystyle \frac{Z_x}{\partial x}|_{x=x_0,y=y_0} ∂xZx∣x=x0,y=y0 或 f x ( x 0 , y 0 ) f_x(x_0,y_0) fx(x0,y0) 3.可微定义设函数 z = f ( x , y ) z = f(x,y) z=f(x,y)在点 ( x , y ) (x,y) (x,y)的某领域内有定义,如果函数在 ( x , y ) (x,y) (x,y)的全增量 Δ z = f ( x + Δ x , y + Δ y ) − f ( x , y ) \Delta z = f(x+\Delta x, y+\Delta y) - f(x,y) Δz=f(x+Δx,y+Δy)−f(x,y) 可表示为 Δ z = A Δ x + B Δ y + o ( ρ ) \Delta z = A\Delta x + B\Delta y + o(\rho) Δz=AΔx+BΔy+o(ρ) 其中A和B不依赖于 Δ x \Delta x Δx 和 Δ y \Delta y Δy而仅与x和y有关, ρ = ( Δ x ) 2 + Δ y ) 2 \rho = \sqrt{(\Delta x)^2 +\Delta y)^2} ρ=(Δx)2+Δy)2 ,那么称函数 z = f ( x , y ) z = f(x,y) z=f(x,y)在点 ( x , y ) (x,y) (x,y)可微分,而 A Δ x + B Δ y A\Delta x + B\Delta y AΔx+BΔy称为函数 z = f ( x , y ) z = f(x,y) z=f(x,y)在点 ( x , y ) (x,y) (x,y)的全微分,记作 d z dz dz,即 d z = A Δ x + B Δ y dz = A\Delta x + B\Delta y dz=AΔx+BΔy 2.三者关系
可导不一定连续 对于不成立的推导,我们只需举出一个反例即可 f ( x , y ) = { x y x 2 + y 2 ( x , y ) ≠ ( 0 , 0 ) 0 ( x , y ) = ( 0 , 0 ) \displaystyle f(x,y)=\begin{cases} \frac{xy}{x^2+y^2} & (x,y) ≠ (0,0) \\ 0 & (x,y) = (0,0) \end{cases} f(x,y)={x2+y2xy0(x,y)=(0,0)(x,y)=(0,0) 由于 f x ′ ( 0 , 0 ) = l i m Δ x → 0 f ( Δ x , 0 ) − f ( 0 , 0 ) Δ x = l i m Δ x → 0 0 − 0 Δ x = 0 \displaystyle f'_x(0,0) = lim_{\Delta x\to 0}\frac{f(\Delta x,0) - f(0,0)}{\Delta x} = lim_{\Delta x\to 0}\frac{0-0}{\Delta x} = 0 fx′(0,0)=limΔx→0Δxf(Δx,0)−f(0,0)=limΔx→0Δx0−0=0 同理 f y ′ ( 0 , 0 ) = 0 \displaystyle f'_y(0,0) = 0 fy′(0,0)=0, 故 ( 0 , 0 ) (0,0) (0,0)点可导, 设点P为聚点,当点P沿着平行于 y = k x y = kx y=kx的方向趋于与 ( 0 , 0 ) (0,0) (0,0)时, l i m x → 0 , y → k x = l i m x → 0 k x 2 x 2 + k 2 x 2 = k 1 + k 2 \displaystyle lim_{ x \to 0, y \to kx} = lim_{ x \to 0}\frac{kx^2}{x^2 + k^2x^2} = \frac{k}{1+k^2} limx→0,y→kx=limx→0x2+k2x2kx2=1+k2k 该极限不存在,则 f ( x , y ) f(x,y) f(x,y)在 ( 0 , 0 ) (0,0) (0,0)点不连续 连续不一定可导 对于不成立的推导,我们只需举出一个反例即可 f ( x , y ) = ∣ x ∣ + ∣ y ∣ \displaystyle f(x,y) = |x| + |y| f(x,y)=∣x∣+∣y∣ 由 l i m x → 0 , y → 0 f ( x , y ) = l i m x → 0 , y → 0 ( ∣ x ∣ + ∣ y ∣ ) = 0 = f ( 0 , 0 ) lim_{x\to0,y\to0}f(x,y) = lim_{x\to0,y\to0}(|x|+|y|) = 0 = f(0,0) limx→0,y→0f(x,y)=limx→0,y→0(∣x∣+∣y∣)=0=f(0,0),知 f ( x , y ) f(x,y) f(x,y)在 ( 0 , 0 ) (0,0) (0,0)点连续 而 f ( x , 0 ) = ∣ x ∣ f(x,0) = |x| f(x,0)=∣x∣在 x = 0 x = 0 x=0处不可导,则 f x ′ ( 0 , 0 ) f_x'(0,0) fx′(0,0)不存在,由对称性知 f y ′ ( 0 , 0 ) f_y'(0,0) fy′(0,0)也不存在,故函数不可导 3.2 可微和偏导可微一定偏导 设函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 P ( x , y ) P(x,y) P(x,y)可微分,于是对于点P的某个领域内的任意一点 P ′ ( x + Δ x , y + Δ y ) P'(x+\Delta x,y+\Delta y) P′(x+Δx,y+Δy)式 Δ z = A Δ x + B Δ y + o ( ρ ) \Delta z = A\Delta x + B\Delta y + o(\rho) Δz=AΔx+BΔy+o(ρ) 总成立。特别的,当 Δ y = 0 \Delta y = 0 Δy=0时, p = ∣ Δ x ∣ p=|\Delta x| p=∣Δx∣,所以上式成为 f ( x + Δ x , y ) − f ( x , y ) = A Δ x + o ( ∣ Δ x ∣ ) f(x+\Delta x, y) - f(x,y) = A\Delta x + o(|\Delta x|) f(x+Δx,y)−f(x,y)=AΔx+o(∣Δx∣) 上式两边各除 Δ x \Delta x Δx,再令 Δ → 0 \Delta \to 0 Δ→0而取极限,就得 l i m Δ x → 0 f ( x + Δ x , y ) − f ( x , y ) Δ x = A \displaystyle lim_{\Delta x \to 0} \frac{f(x+\Delta x, y) - f(x,y)}{\Delta x} = A limΔx→0Δxf(x+Δx,y)−f(x,y)=A 从而偏导数 ∂ f ∂ x \displaystyle \frac{\partial f}{\partial x} ∂x∂f存在,且等于A,同理可证 ∂ z ∂ x = B \displaystyle \frac{\partial z}{\partial x} = B ∂x∂z=B,证毕 偏导不一定可微 对于不成立的推导,我们只需举出一个反例即可 f ( x , y ) = { x y x 2 + y 2 ( x , y ) ≠ ( 0 , 0 ) 0 ( x , y ) = ( 0 , 0 ) \displaystyle f(x,y)=\begin{cases} \displaystyle \frac{xy}{\sqrt{x^2+y^2}} & (x,y) ≠ (0,0) \\ 0 & (x,y) = (0,0) \end{cases} f(x,y)=⎩ ⎨ ⎧x2+y2 xy0(x,y)=(0,0)(x,y)=(0,0) 由于 f x ′ ( 0 , 0 ) = l i m Δ x → 0 f ( Δ x , 0 ) − f ( 0 , 0 ) Δ x = l i m Δ x → 0 0 − 0 Δ x = 0 \displaystyle f'_x(0,0) = lim_{\Delta x\to 0}\frac{f(\Delta x,0) - f(0,0)}{\Delta x} = lim_{\Delta x\to 0}\frac{0-0}{\Delta x} = 0 fx′(0,0)=limΔx→0Δxf(Δx,0)−f(0,0)=limΔx→0Δx0−0=0 同理 f y ′ ( 0 , 0 ) = 0 \displaystyle f'_y(0,0) = 0 fy′(0,0)=0, 故 ( 0 , 0 ) (0,0) (0,0)点可导,但 l i m Δ x → 0 , Δ y → 0 [ f ( Δ x , Δ y ) − f ( 0 , 0 ) ] − [ f x ′ ( 0 , 0 ) Δ x + f y ′ ( 0 , 0 ) Δ y ] ρ = l i m Δ x → 0 , Δ y → 0 Δ x Δ y ( Δ x ) 2 + ( Δ y ) 2 \displaystyle lim_{\Delta x \to 0,\Delta y \to 0}\frac{[f(\Delta x,\Delta y) - f(0,0)] - [f_x'(0,0)\Delta x + f_y'(0,0)\Delta y]}{\rho} = lim_{\Delta x \to 0,\Delta y \to 0}\frac{\Delta x \Delta y}{(\Delta x)^2 + (\Delta y)^2} limΔx→0,Δy→0ρ[f(Δx,Δy)−f(0,0)]−[fx′(0,0)Δx+fy′(0,0)Δy]=limΔx→0,Δy→0(Δx)2+(Δy)2ΔxΔy 设 g ( x , y ) = x y x 2 + y 2 \displaystyle g(x,y) = \frac{xy}{x^2+y^2} g(x,y)=x2+y2xy, 设点P为聚点,当点P沿着平行于 y = k x y = kx y=kx的方向趋于与 ( 0 , 0 ) (0,0) (0,0)时, l i m x → 0 , y → k x = l i m x → 0 k x 2 x 2 + k 2 x 2 = k 1 + k 2 \displaystyle lim_{ x \to 0, y \to kx} = lim_{ x \to 0}\frac{kx^2}{x^2 + k^2x^2} = \frac{k}{1+k^2} limx→0,y→kx=limx→0x2+k2x2kx2=1+k2k,该极限不存在,则 f ( x , y ) f(x,y) f(x,y)在 ( 0 , 0 ) (0,0) (0,0)点不可微 3.3 可微和连续可微一定连续 若 z = f ( x , y ) z = f(x,y) z=f(x,y)在点 ( x , y ) (x,y) (x,y)可微分,那么由微分的定义有 l i m ρ → 0 Δ z = 0 lim_{\rho \to 0}\Delta z = 0 limρ→0Δz=0 从而 l i m Δ x → 0 , Δ y → 0 = f ( x + Δ x , y + Δ y ) = l i m ρ → 0 [ f ( x , y ) + Δ z ] = f ( x , y ) lim_{\Delta x \to 0,\Delta y \to 0}= f(x+\Delta x, y+\Delta y) = lim_{\rho \to 0}[f(x,y) + \Delta z] = f(x,y) limΔx→0,Δy→0=f(x+Δx,y+Δy)=limρ→0[f(x,y)+Δz]=f(x,y) 因此 z = f ( x , y ) z = f(x,y) z=f(x,y)在点 ( x , y ) (x,y) (x,y)处连续 连续不一定可微 同上举反例即可 f ( x , y ) = ∣ x ∣ + ∣ y ∣ \displaystyle f(x,y) = |x| + |y| f(x,y)=∣x∣+∣y∣ 由3.1.2知 f ( x , y ) f(x,y) f(x,y)在 ( 0 , 0 ) (0,0) (0,0)点连续且函数不可导,而因为偏导存在是全微分的必要条件, 因此也不可微 4.记忆方法
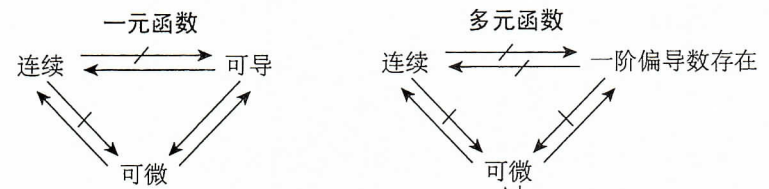
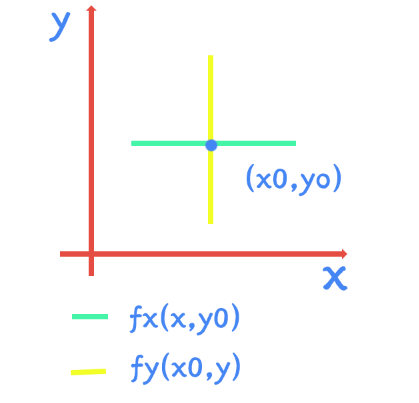
与一元函数连续可导可微对比记忆即可(一元函数关系可参考笔者上一篇文章), 两者的区别在于 多元函数偏导(可导)推不出连续多元函数偏导(可导)推不出可微其余部分都相同,那么为什么二元函数偏导推不出连续和可微呢? 下面从几何角度证明 函数可导,即偏导数 f x ( x 0 , y 0 ) f_x(x_0,y_0) fx(x0,y0), f y ( x 0 , y 0 ) f_y(x_0,y_0) fy(x0,y0)存在 而 f x ( x 0 , y 0 ) f_x(x_0,y_0) fx(x0,y0)本质上是 f ( x , y 0 ) f(x,y_0) f(x,y0)函数的导数,把 y y y用 y 0 y_0 y0代进去,现在只有 x x x在变化,而 x x x在变化的时候,只能在 y = y 0 y=y_0 y=y0的线上变化, 如下图 f x ( x , y 0 ) f_x(x,y_0) fx(x,y0) 这说明这点偏导数只跟这个二元函数沿 y = y 0 y=y_0 y=y0这条线上函数值有关 同理,代入 x 0 x_0 x0,这点的另一个偏导数只跟二元函数沿 x = x 0 x=x_0 x=x0这条线上函数值有关, 如下图 f y ( x 0 , y ) f_y(x_0,y) fy(x0,y)
以上说明两个偏导数只跟过 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)点平行于两个坐标轴的十字线有关. 但连续是要求动点以任意方式趋向 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)的极限等于 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)点函数值 f ( x 0 , y 0 ) f(x_0,y_0) f(x0,y0). 故十字线上的函数值决定不了函数的重极限 同理,决定不了全微分 5.参考文章 高等数学第七版下册武忠详辅导讲义 |
【本文地址】
今日新闻 |
推荐新闻 |