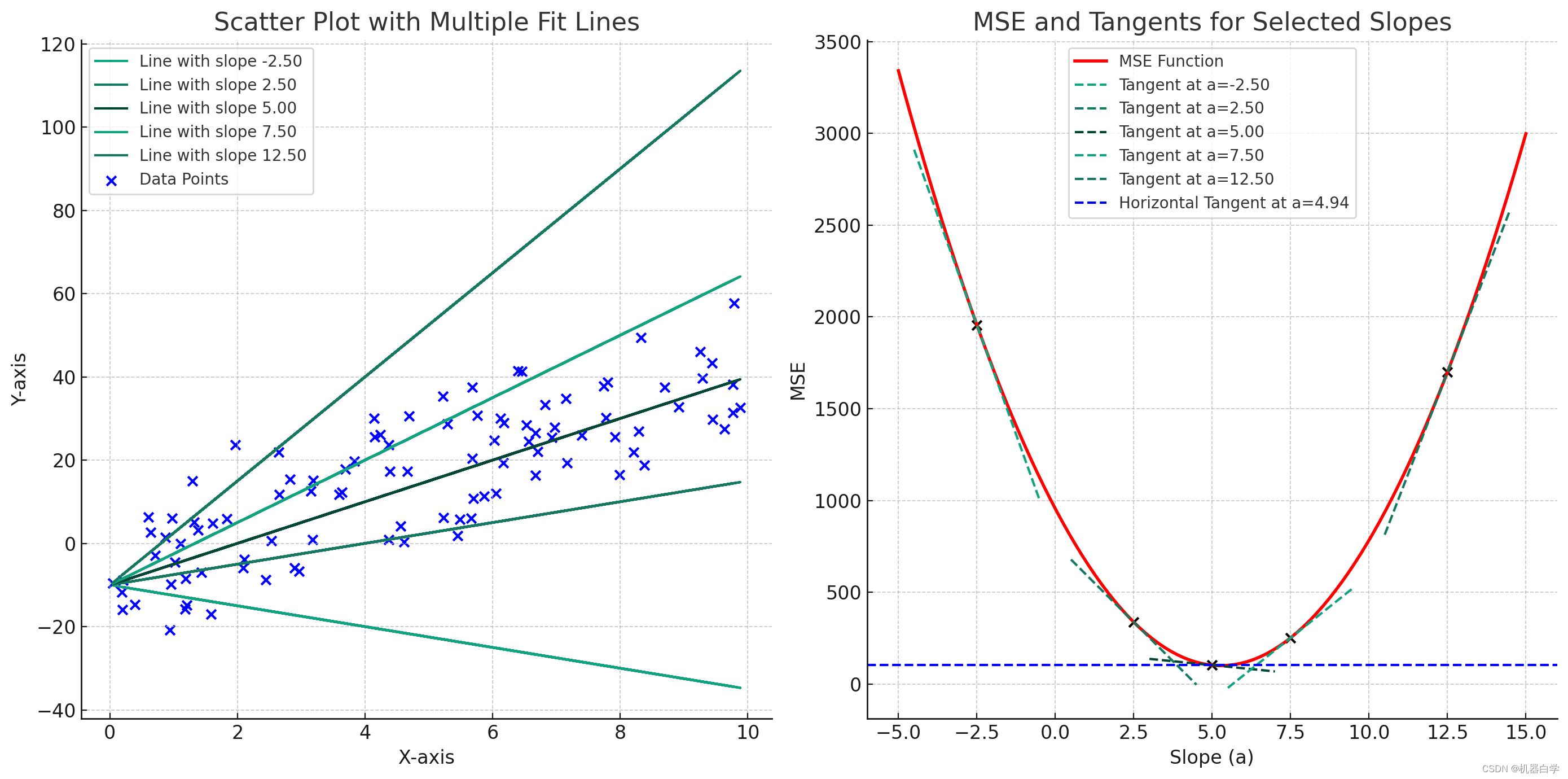
目录

二、从线性模型开始：回归

 3.回归损失函数求导

        （1）梯度下降法

        （2）直接求导法

        在之前的文章中我们介绍了回归问题损失函数的推导，现在已知损失函数，想要使用损失函数来更新模型参数以实现最优化，就要涉及损失函数的求导问题了。

        回归损失函数推导文章地址：https://blog.csdn.net/qq_58718853/article/details/137536043

        机器学习的过程是对损失函数求导，然后根据导数优化参数的过程。因为损失函数衡量的是模型输出和实际数据的差异，因此我们希望这个差异值越小越好。对于回归函数的损失函数MSE来说，它具有很好的数学性质。

        MSE损失函数是机器学习中不多的有唯一最优解的。MSE是一个凸（凸向x轴）函数，意味着有一个全局最小值。如下右图所示，像一个抛物线。

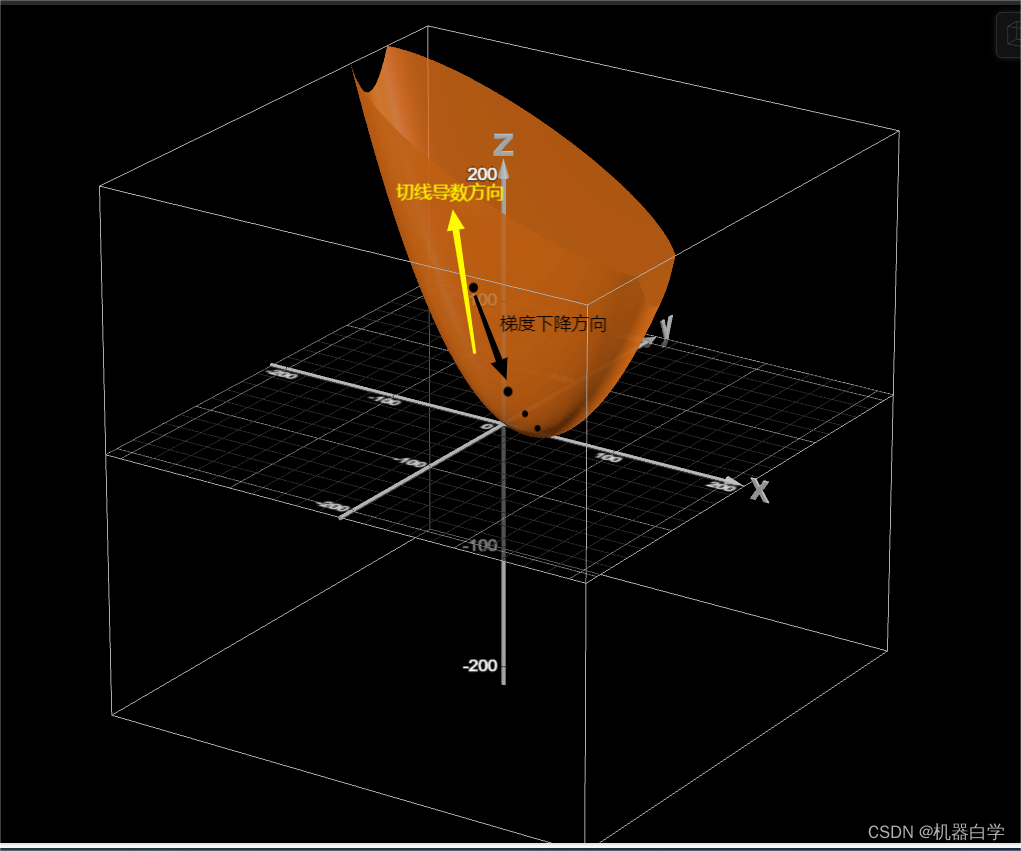
        其特性意味着我们可以根据中学知识，直接对损失函数求导取零，其对应的参数值就是最优曲线的参数。这是非常特殊的，更常见的是梯度优化方式。

        如上图，从一个随机的线出发，其对应于损失函数上一点（x轴代表该线的斜率参数，y值是损失函数值），假设其在最低点左侧，我们可以看到左侧所有点对应的导数（虚线：过该点损失曲线的切线斜率）都是负数。

        需注意损失函数是关于参数的函数，因此图中x轴代表的含义是模型参数。在梯度下降法中，参数是减去梯度，因此梯度负数代表模型参数是不断增加。在最优点左侧，模型参数增加可以理解为损失函数上的点不断向右下移动，不断逼近最优点。右侧同理。在最低的梯度为零，没有移动的趋势，处于稳定。

        进一步理解是，梯度下降法就像是“有老师监督的持续学习”，损失函数的导数就是“老师”，其正负告模型是学习的偏“右”了，还是偏“左”了，此时模型的参数就会根据“老师的指导”，在数轴上往对应相反（正确）的方向移动。直到到达最优模型，也是损失函数最低点时，“老师闭嘴了”（损失函数求导为0。模型参数就固定下来了。下式为具体的梯度更新公式， 为学习率，用于控制更新的速率。

        其实之前图例是一个简化的版本，其假设模型参数只有一个。但实际的模型参数是一个向量甚至矩阵，实际的损失函数图像十分复杂，需要升到更高维度的空间，下图给出一个比较简单的两个参数 的例子。先给出损失函数形式如下。

        下图可以看到梯度下降方向和求导方向相反，因此参数更新公式中使用减号。

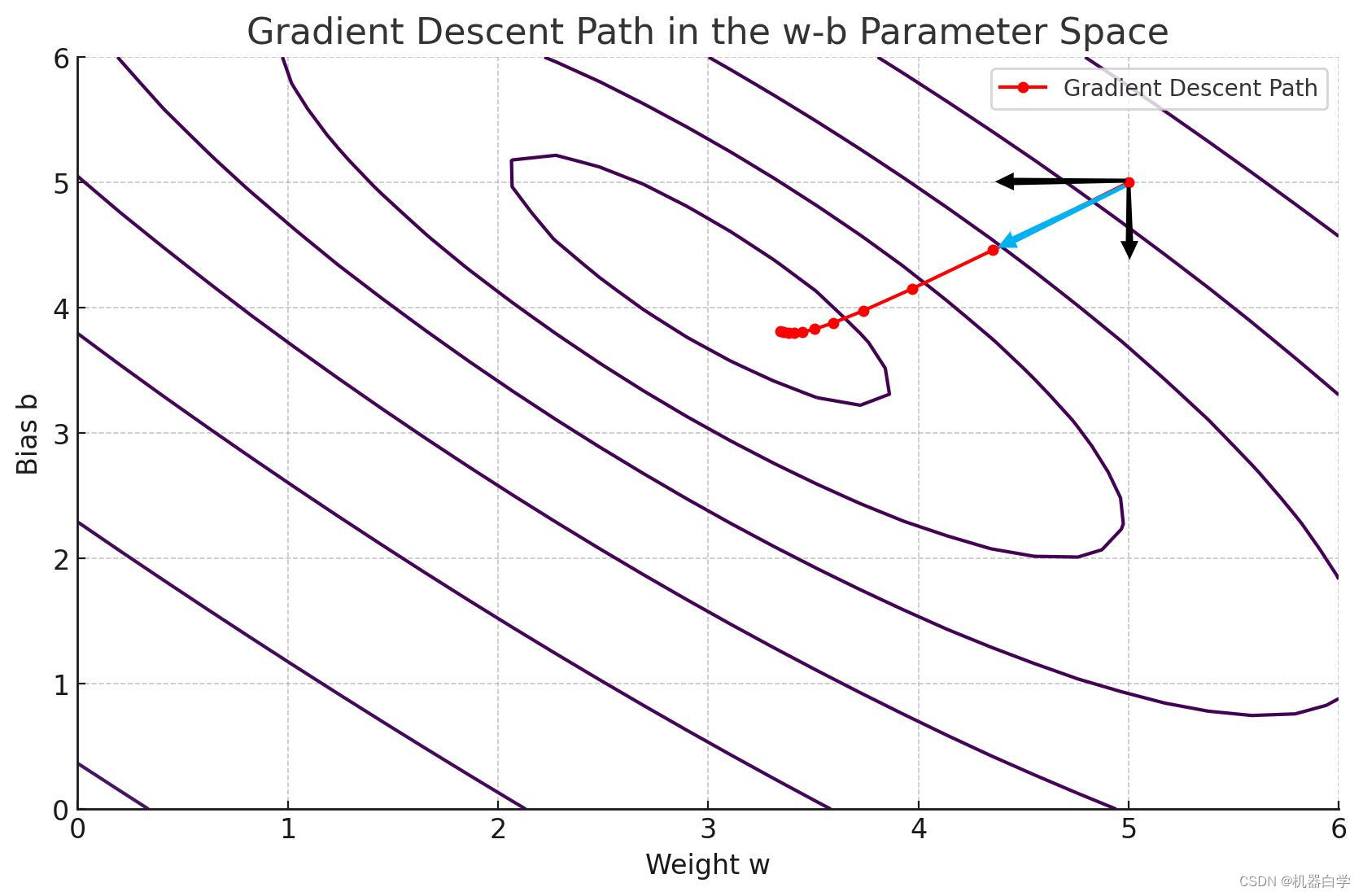
        将上图梯度下降过程投影到二维平面（俯视视角），可以进一步看清不同的参数 对于梯度下降的不同分量影响。

        之前提到MSE损失函数有一种简单有效的方法快速求解最优模型参数，即将损失函数求导然后取零，其对应的参数值就是是损失最小的最优模型参数。相较梯度下降法的迭代过程，直接求导“一步到位”。下面给出其数学求导公式推导过程。

① MSE损失函数转为矩阵形式：

         之前的似然函数和最小二乘法都推出过MSE损失函数的标准形式如下。

        假如将 视为一个整体 ，即定义一个矩阵A

        那么 等价于标准形式中实现的对每个样本差的平方求和。

        可以看出标准形式Loss损失函数和新构建矩阵 只差取样本平均的关系，具体如下。

        对于矩阵 ，定义两个矩阵为样本集 和预测集

                                          ,    

        此处，再将 进一步展开成关于模型参数 和样本特征输入 的式子。对于这里的每一个样本 ，我们可以将其合并成一个大矩阵，代表整个数据集的特征空间矩阵。

        假设将每个样本的特征向量按行横向依次拼接，即构建一个大矩阵 。

        因为每个样本特征维有(n+1)（多的一个是加入的误差项）个（矩阵行数），数据集一共有N个样本（矩阵列数），因此矩阵形状为（n+1）*N。注意此时小x上下标含义：x上标代表是第几个样本的数据，下标代表当前数据的第几维的特征值。

                                      ⬇（上标N）：第N个样本的数据：第N套房源数据

展开式中小 x 举例： 

                                      ⬆（下标 n）：第N个样本中第n维特征值：n代表房屋面积维度

        注意：如果按上述设计大矩阵 ，对 的拆解处理在后续的运算过程中，要进行相应的维度数的变化，以匹配其中 运算后的到的矩阵维度数。

        此时设计的大矩阵跟模型参数乘积 得到的预测值 。需特别注意此处 的含义，是区别于定义回归模型时使用的特征向量 ，此处是一个矩阵，代表了全体样本的特征值，是整个数据的矩阵形式，如上述定义。但此时矩阵计算，导致最终结果 维度发生了变化。具体可以看下述 和 的对比。其实只是对结果做了一个转置处理。

        可以看出 和 是转置关系，因此可以最终得到 和模型参数 和数据特征集矩阵 的关系为下。

        根据矩阵 的定义，存在以下关系。

        将上式代入Loss和A的关系式，可得到损失函数的矩阵形式。

                MSE损失函数矩阵形式：

        关键的模型参数 “藏”在 中；虽然式子右侧都是矩阵，但是最后经过矩阵运算可以检验最后得出的结果是一个“标量”，即一个数，这和标准形式的损失函数契合。

②MSE损失函数的矩阵求导讨论

        下面对上述矩阵形式的损失函数进行求导讨论。

矩阵求导方法：“XY”拉伸术         1.标量（一个值）不变，向量拉伸

        2.“Y”横向拉伸，“X”纵向拉伸

eg: 假设函数 ，其中都是向量，代表这个函数输入多变量，输出多值。

                                 （横向拉伸）

                                                                                          （纵向拉伸）

        可以看到Y向量下的每一个分量被放在“横向”，X下的每一个变量放在“纵向”上，Y,X对应的分量都是单一标量，可以求出偏导，这样构成的偏导矩阵就是对Y求X偏导结果。

        将矩阵形式的损失函数回到之前跟 矩阵的关系式，此时损失是一个标量，因为最后得到的是一个值（所有样本损失的平方和）。但 是一个矩阵（向量），根据矩阵求导方法：XY拉伸术第一条，不需要对 (Y)做处理，但需要将 （X)纵向拉伸。

                                                                                            （纵向拉伸）

        通过 的定义，我们可以将 表达式展开写出来。

        那么对每个 的偏导就显而易见了。

        提出公因数 ，将其代入偏导矩阵 。

        可以看到，如果忽略掉常数，其实可以得到一个矩阵求导的公式，即

        这里多出一个常数2，为了计算方便，同时不影响损失函数优化的本质，可以改进我们的损失函数得到损失函数的求导矩阵形式。

                MSE损失函数求导矩阵形式：

        仅仅在式子前多乘以一个1/2，用于抵消求导过程中的2倍值作用。

③MSE损失函数的求导链式法则

求导链式法则：

        假设 Z=f(X)，Y=g(X)，则存在关系式

        在矩阵求导中，对一个向量求向量导，使用链式法则时可能存在维度方向不匹配的情况，需要交换调整乘法次序。因此矩阵乘法与普通链式法则的乘法顺序相反。

         我们关心的是关于参数的导数，根据链式法则，可得已知条件如下。

        那么根据已知条件，我们现在需要关心的就是根据求导链式法则得到的损失函数求导中的 和 具体计算结果。

        计算 ，根据矩阵求导方法，首先确定 都为向量。

        因此需要对Y（）横向拉伸，对X（）纵向拉伸。上述矩阵内已给出各分量 和各分量 的等式关系。因此可以直接写出各分量求导结果如下。

        是对角线全为1的矩阵。

        计算 ，可确定 都为向量。这里对于 回归到最初的定义形式，方便对分量展开。

        同理需要对Y（）横向拉伸，对X（）纵向拉伸。此处也要将 的具体式展开。

        此时使用XY拉伸术，求导结果如下。

        可以发现求导结果恰好就是我们之前定义的数据特征集大矩阵 。可以将这个结果代入矩阵公式中，得到一个矩阵求导的通式。

        最终，将 , 结果代入，可得求导结果。

④MSE的矩阵二阶导的凸性保证

        在梯度下降法中，我们给出了MSE损失函数的图像（一个开口向上的抛物线），此时损失函数是凸的，因此导数等于零时有唯一最小解。但是并没有证明损失函数一定是凸的，因此对于直接求导法对导数取零以算出最优参数前，还需证明损失函数是凸的，即导数等于零的点一定是函数唯一的最小值点，而不是局部极小值。这需要二阶导来判断。

        对上述一阶导结果 ，我们再对 求导，首先先将一阶导结果展开，跟 相关的项只有 ,根据我们之前总结的公式，可以将 ()视作一个整体，因此可以直接计算出损失函数的二阶导如下。

        现在来研究一下这个二阶导矩阵的形状， 是一个（n+1)*N 的矩阵，因此 是一个（n+1)*(n+1) 的矩阵。这个二阶导矩阵被称为Hessian矩阵，只要可以证明其是正定矩阵，则说明损失函数是严格的凸函数。

正定矩阵：对于实对称方阵 ，满足 ，则为正定矩阵

矩阵合同：存在可逆矩阵 ，使得 ，则 合同

合同、二次型与正定性：合同，其二次型也相等，即 ，则 具有相同正定性。

        观测二阶导结果，可知一定存在可逆矩阵 ，使得二阶导结果 合同于单位阵 ，而单位阵一定是正定矩阵，说明二阶导也是正定的，损失函数一定是凸的，因此可以直接对一阶导取零得出唯一的最小值点。

        终于，我们可以取一阶导为零，然后得到模型的最优解。

        这意味着我们如果使用线性模型，已知训练的特征数据和目标数据，我们马上就可以根据上式得到最优的模型参数（回归模型各个权值）。