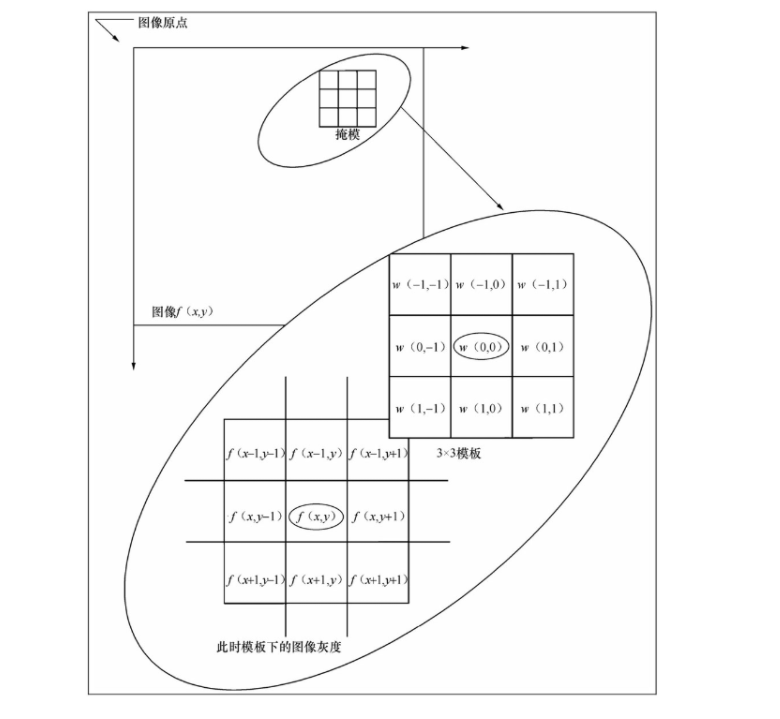
滤波是信号处理中的一个概念，是将信号中特定波段频率滤除的操作，在数字信号处理中通常通过傅里叶变换及其逆变换实现。由于空间域滤波实际上和通过傅里叶变换实现的频域下的滤波是等效的，故而也称为滤波。不同的是空间域滤波主要直接基于邻域（空间域）对图像中像素执行计算。

对图像中的每一点 ( x , y ) (x, y) (x,y)，重复下面的操作。

（1）对预先定义的以 （ x , y ） （x, y） （x,y）为中心的邻域内的像素进行运算。

（2）将（1）中运算的结果作为 （ x , y ） （x, y） （x,y）点新的响应。

上述过程就称为邻域处理或空间域滤波。一幅数字图像可以看成一个二维函数 f ( x , y ) f(x, y) f(x,y)，而 x − y x-y x−y平面表明了空间位置信息，称为空间域，基于 x − y x-y x−y空间邻域的滤波操作叫作空间域滤波。如果对于邻域中的像素计算为线性运算，则又称为线性空间域滤波，否则称为非线性空间域滤波。

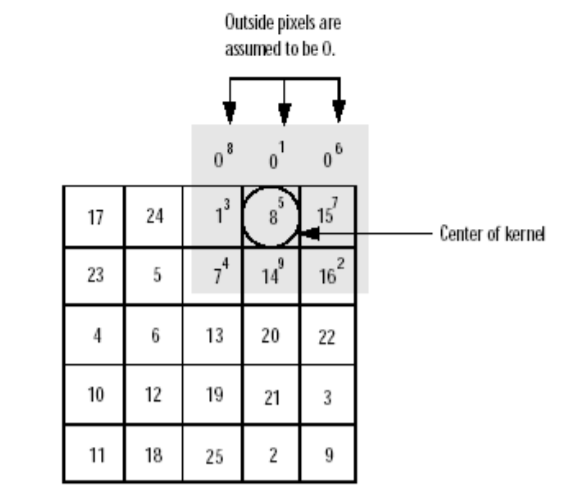
下图直观地展示了用一个3× 3的模板（又称为滤波器、模板、掩模、核或者窗口）进行空间滤波的过程，模板为 w w w，用黑笔圈出的 w ( 0 , 0 ) w(0,0) w(0,0)是其中心。

滤波过程就是在图像 f ( x , y ) f (x, y) f(x,y)中逐点地移动模板，使模板中心和点 ( x , y ) (x, y) (x,y)重合。在每一点 （ x , y ） （x, y） （x,y）处，滤波器在该点的响应是根据模板的具体内容并通过预先定义的关系来计算。一般来说模板中的非0元素指出了邻域处理的范围，只有那些当模板中心与点 （ x , y ） （x, y） （x,y）重合时，图像 f f f中和模板中非0像素重合的像素参与了决定点 （ x , y ） （x, y） （x,y）像素值的操作。

在线性空间滤波中模板的系数则给出了一种加权模式，即 （ x , y ） （x, y） （x,y）处的响应由模板系数与模板下面区域的相应 f f f的像素值的乘积之和给出。例如，在上图中，对于模板的响应 R R R为： R = w ( − 1 , − 1 ) f ( x − 1 , y − 1 ) + w ( − 1 , 0 ) f ( x − 1 , y ) + … + w ( 0 , 0 ) f ( x , y ) + … + w ( 1 , 0 ) f ( x + 1 , y ) + w ( 1 , 1 ) f ( x + 1 , y + 1 ) R=w(-1, -1) f (x-1, y-1) + w(-1, 0) f (x-1, y) + …+ w(0, 0) f (x, y) +…+ w(1, 0) f (x+1, y) + w(1, 1)f(x+1, y+1) R=w(−1,−1)f(x−1,y−1)+w(−1,0)f(x−1,y)+…+w(0,0)f(x,y)+…+w(1,0)f(x+1,y)+w(1,1)f(x+1,y+1)

更一般的情况，对于一个大小为 m × n m×n m×n的模板，其中 m = 2 a + 1 , n = 2 b + 1 m=2a+1, n=2b+1 m=2a+1,n=2b+1, a , b a, b a,b均为正整数，即模板长与宽均为基数，且可能的最小尺寸为3× 3（偶数尺寸的模板由于其不具有对称性因而很少被使用，而1× 1大小的模板的操作不考虑邻域信息，退化为图像点运算），可以将滤波操作形式化地表示为： g ( x , y ) = ∑ s = − a a ∑ t = − b b w ( s , t ) f ( x + s , y + t ) g(x, y)=\sum_{s=-a}^{a} \sum_{t=-b}^{b} w(s, t) f(x+s, y+t) g(x,y)=s=−a∑a​t=−b∑b​w(s,t)f(x+s,y+t)

对于大小为 M × N M×N M×N的图像 f ( 0 , … , M − 1 , 0 , … , N − 1 ) f (0, …, M-1,0, …, N-1) f(0,…,M−1,0,…,N−1)，对 x = 0 , 1 , 2 , … , M − 1 x=0,1,2, …, M-1 x=0,1,2,…,M−1和 y = 0 , 1 , 2 , … , N − 1 y=0,1,2, …,N-1 y=0,1,2,…,N−1依次应用公式，从而完成了对于图像 f f f所有像素的处理，得到新的图像 g g g。

执行滤波操作要注意的一点是当模板位于图像边缘时，会产生模板的某些元素很可能会位于图像之外的情况，这时，对于在边缘附近执行滤波操作需要单独处理，以避免引用到本不属于图像的无意义的值。

以下3种策略都可以用来解决边界问题。

（1）收缩处理范围——处理时忽略位于图像 f f f边界附近会引起问题的那些点。 设原图像为： [ 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 4 4 4 4 4 ] \left[\begin{array}{lllll}1 & 1 & 1 & 1 & 1 \\2 & 2 & 2 & 2 & 2 \\3 & 3 & 3 & 3 & 3 \\4 & 4 & 4 & 4 & 4\end{array}\right] ⎣⎢⎢⎡​1234​1234​1234​1234​1234​⎦⎥⎥⎤​ 对于原图像中所使用的模板，处理时忽略图像四周一圈1个像素宽的边界： [ − − − − − − 2 2 2 − − 3 3 3 − − − − − − ] \left[\begin{array}{cccc}- & - & - & - & - \\- & 2 & 2 & 2 & - \\- & 3 & 3 & 3 & - \\- & - & - & -&-\end{array}\right] ⎣⎢⎢⎡​−−−−​−23−​−23−​−23−​−−−−​⎦⎥⎥⎤​

" -"表示无法进行模板操作的像素点。

从而确保了滤波过程中模板始终不会超出图像的边界。

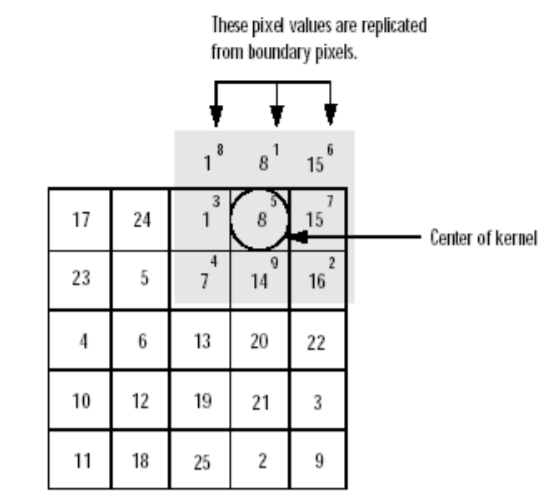
2）使用常数填充图像——根据模板形状为图像 f f f虚拟出边界，虚拟边界像素值为指定的常数，如0，得到虚拟图像 f ′ f ' f′，保证模板在移动过程中始终不会超出 f ′ f ' f′的边界。

（3）使用复制像素的方法填充图像——和（2）基本相同，只是用来填充虚拟边界像素值的不是固定的常数，而是复制图像 f f f本身边界的模式。

上述的滤波操作实际是信号处理中的互相关操作，互相关和卷积的略有不同，卷积表示如下。 g ( x , y ) = ∑ s = − a a ∑ t = − b b w ( − s , − t ) f ( x + s , y + t ) g(x, y)=\sum_{s=-a}^{a} \sum_{ t=-b}^{b} w(-s,-t) f(x+s, y+t) g(x,y)=s=−a∑a​t=−b∑b​w(−s,−t)f(x+s,y+t)

两者尽管差别细微，但有本质不同，卷积在卷积时模板是相对其中心点做镜像后再对 f f f位于模板下的子图像做加权和的，或者说在做加权和之前模板先要以其中心点为原点旋转180°。如果忽略了这一细微差别将导致完全错误的结果，只有当模板本身是关于中心点对称时，互相关和卷积的结果才会相同。

g ( x , y ) = ∑ s = − a a ∑ s = − b b w ( s , t ) f ( x + s , y + t ) ∑ s = − a a ∑ s = − b b w ( s , t ) g(x,y)=\frac{\sum_{s=-a}^a \sum_{s=-b}^bw(s,t)f(x+s,y+t)}{\sum_{s=-a}^a \sum_{s=-b}^b w(s,t)} g(x,y)=∑s=−aa​∑s=−bb​w(s,t)∑s=−aa​∑s=−bb​w(s,t)f(x+s,y+t)​

模板大小为 m × n m\times n m×n( m , n m,n m,n为奇数)，则 a = m − 1 2 , a = n − 1 2 a=\frac{m-1}{2},a=\frac{n-1}{2} a=2m−1​,a=2n−1​。 f ( x , y ) f(x,y) f(x,y)为原图像在 ( x , y ) (x,y) (x,y)的像素点； g ( x , y ) g(x,y) g(x,y)为滤波后得到的在 ( x , y ) (x,y) (x,y)的像素点。

g ( x , y ) = [ ∏ ( s , t ) ∈ S x y f ( s , t ) ] 1 m ⋅ n g(x,y)=[\prod_{(s,t)\in S_{xy}}f(s,t)]^{\frac{1}{m\cdot n}} g(x,y)=[(s,t)∈Sxy​∏​f(s,t)]m⋅n1​

模板大小为 m × n m\times n m×n， f ( x , y ) f(x,y) f(x,y)为原图像在 ( x , y ) (x,y) (x,y)的像素点； g ( x , y ) g(x,y) g(x,y)为滤波后得到的在 ( x , y ) (x,y) (x,y)的像素点。 S x , y S_{x,y} Sx,y​为以 ( x , y ) (x,y) (x,y)为中心的含有奇数个像素点的邻域窗口；

和算术均值滤波器相比，几何均值滤波器能够更好的去除高斯噪声，并且能够更多的保留图像的边缘信息。但其对0值是非常敏感的，在滤波器的窗口内只要有一个像素的灰度值为0，就会造成滤波器的输出结果为0。

g ( x , y ) = m n ∑ s , t ∈ S x , y 1 f ( x , y ) g(x,y)=\frac{mn}{\sum_{s,t\in S_{x,y}}\frac{1}{f(x,y)}} g(x,y)=∑s,t∈Sx,y​​f(x,y)1​mn​

模板大小为 m × n m\times n m×n， f ( x , y ) f(x,y) f(x,y)为原图像在 ( x , y ) (x,y) (x,y)的像素点； g ( x , y ) g(x,y) g(x,y)为滤波后得到的在 ( x , y ) (x,y) (x,y)的像素点。 S x , y S_{x,y} Sx,y​为以 ( x , y ) (x,y) (x,y)为中心的含有奇数个像素点的邻域窗口；

谐波均值滤波器对盐粒噪声（白噪声）效果较好，不适用于胡椒噪声；也比较适合处理高斯噪声。

g ( x , y ) = ∑ s , t ∈ S x , y f ( s , t ) Q + 1 ∑ s , t ∈ S x , y f ( s , t ) Q g(x,y)=\frac{\sum_{s,t\in S_{x,y}}f(s,t)^{Q+1}}{\sum_{s,t\in S_{x,y}}f(s,t)^{Q}} g(x,y)=∑s,t∈Sx,y​​f(s,t)Q∑s,t∈Sx,y​​f(s,t)Q+1​

其中 Q Q Q称为滤波器的阶数。当 Q Q Q是正数时，滤波器用于消除“椒”噪声;当 Q Q Q是负数时，滤波器用于消除“盐”噪声。但它不能同时消除这两种噪声。 当 Q = 0 Q=0 Q=0，逆谐波均值滤波器转变为算术均值滤波器;当 Q = − 1 Q=-1 Q=−1，逆谐波均值滤波器转变为谐波均值滤波器。

g ( x , y ) = M e d ( s , t ) ∈ S x , y { f ( s , t ) } g(x,y)=Med_{(s,t)\in S_{x,y}}\{f(s,t)\} g(x,y)=Med(s,t)∈Sx,y​​{f(s,t)}

式中 f ( x , y ) f(x,y) f(x,y)为原图像在 ( x , y ) (x,y) (x,y)的像素点； S x y S_{xy} Sxy​为以像素 f ( x , y ) f(x,y) f(x,y)为中心的含有奇数个像素点的邻域窗口； g ( x , y ) g(x,y) g(x,y)为滤波后得到的在 ( x , y ) (x,y) (x,y)的像素点, M e d Med Med为取中值。

适于处理椒盐噪声，通过多次使用小模板，可以获得很好的去噪效果，但多次应用中值滤波器,会使图像模糊。

g ( x , y ) = max ⁡ ( s , t ) ∈ S x , y { f ( s , t ) } g(x,y)=\max_{(s,t)\in S_{x,y}}\{f(s,t)\} g(x,y)=(s,t)∈Sx,y​max​{f(s,t)}

式中 f ( x , y ) f(x,y) f(x,y)为原图像在 ( x , y ) (x,y) (x,y)的像素点； S x y S_{xy} Sxy​为以像素 f ( x , y ) f(x,y) f(x,y)为中心的含有奇数个像素点的邻域窗口； g ( x , y ) g(x,y) g(x,y)为滤波后得到的在 ( x , y ) (x,y) (x,y)的像素点, m a x max max为取最大值。

最大值滤波器对于 “椒” 噪声具有较好的消除效果，对于 “盐” 噪声则效果不好。

g ( x , y ) = min ⁡ ( s , t ) ∈ S x , y { f ( s , t ) } g(x,y)=\min_{(s,t)\in S_{x,y}}\{f(s,t)\} g(x,y)=(s,t)∈Sx,y​min​{f(s,t)}

式中 f ( x , y ) f(x,y) f(x,y)为原图像在 ( x , y ) (x,y) (x,y)的像素点； S x y S_{xy} Sxy​为以像素 f ( x , y ) f(x,y) f(x,y)为中心的含有奇数个像素点的邻域窗口； g ( x , y ) g(x,y) g(x,y)为滤波后得到的在 ( x , y ) (x,y) (x,y)的像素点, m i n min min为取最小值。

最小值滤波器对于 “盐” 噪声具有较好的消除效果，对于 “椒” 噪声则效果不好。

本文只使用椒盐噪声和高斯噪声，更多噪声添加可参见： 图像噪声模型