表格/列表法之分部积分 |
您所在的位置:网站首页 › 公式法什么时候用 › 表格/列表法之分部积分 |
表格/列表法之分部积分
|
在求积分的过程中,我们经常使用微积分里的分布积分法,但对于一些复杂的函数,需要运用多次分布积分,比如你可能见过这样的, 求
C
n
=
2
l
∫
0
l
x
(
l
−
x
)
s
i
n
n
π
x
l
d
x
Cn =\frac{2}{l}\int_0^l x(l-x)sin\frac{nπx}{l}dx
Cn=l2∫0lx(l−x)sinlnπxdx 正常计算: C n = [ x ( l − x ) ( − 2 n π c o s n π x l ) − ( l − 2 x ) ( − 2 l n 2 π 2 s i n n π x l ) ] ∣ l 0 ∣ + Cn=\left[x(l-x)(-\frac{2}{nπ}cos\frac{nπx}{l})\right.\\-(l-2x)(-\frac{2l}{n^2π^2}sin\frac{nπx}{l})]\begin{vmatrix} l \\ 0\end{vmatrix}+ Cn=[x(l−x)(−nπ2coslnπx)−(l−2x)(−n2π22lsinlnπx)]∣∣∣∣l0∣∣∣∣+ ( − 1 ) 2 ∫ 0 l ( − 2 ) − 2 l n 2 π 2 s i n n π x l d x (-1)^2\int_0^l(-2) \frac{-2l}{n^2π^2}sin\frac{nπx}{l}dx (−1)2∫0l(−2)n2π2−2lsinlnπxdx = 0 − 4 l 2 n 3 π 3 c o s n π x l ∣ l 0 ∣ =0-\frac{4l^2}{n^3π^3}cos\frac{nπx}{l}\begin{vmatrix} l \\ 0\end{vmatrix} =0−n3π34l2coslnπx∣∣∣∣l0∣∣∣∣ = 4 l 2 n 3 π 3 ( 1 − c o s n π ) =\frac{4l^2}{n^3π^3}(1-cosnπ) =n3π34l2(1−cosnπ) 如果还不太懂可以看一下文章开头的那个例子,自己算一下 运用表格法只需进行对被积函数进行求导积分运算,一步得结果,大大减少了出错率。
|
【本文地址】
今日新闻 |
推荐新闻 |
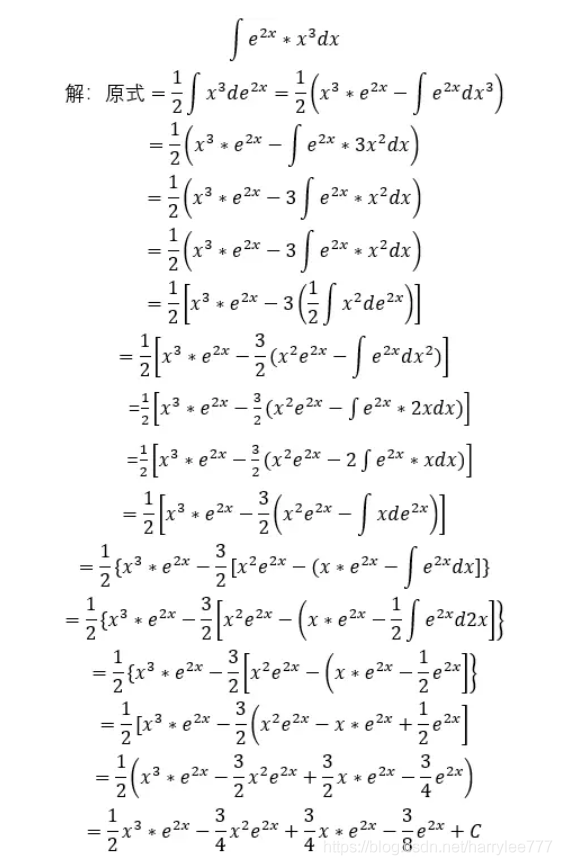 处理起来很是头疼,然而用表格法就能起到这样的效果
处理起来很是头疼,然而用表格法就能起到这样的效果 
 下面说明一下如何使用这种方法 对积分
∫
v
u
d
x
\int vu\,dx
∫vudx 列成表格
下面说明一下如何使用这种方法 对积分
∫
v
u
d
x
\int vu\,dx
∫vudx 列成表格  第一行表示求导,第二行求原函数。 表中内容可分为三部分,连线的地方将他们相乘 图中红色地方表示正 比如
v
∫
u
d
x
,
v
′
′
∫
∫
∫
u
d
x
v\int u\,dx,v''\int\int\int u\,dx
v∫udx,v′′∫∫∫udx 图中黑色地方表示负 比如
−
v
′
∫
∫
u
d
x
-v'\int\int u\,dx
−v′∫∫udx 绿色地方表示
(
−
1
)
n
∫
(
v
n
(
∫
)
n
u
)
d
x
(-1)^n\int (v^n(\int)^nu)dx
(−1)n∫(vn(∫)nu)dx 注意:这里的n表示求导或积分的总次数 最后把这三部分加起来即可,不理解的话请看下面这个例子
第一行表示求导,第二行求原函数。 表中内容可分为三部分,连线的地方将他们相乘 图中红色地方表示正 比如
v
∫
u
d
x
,
v
′
′
∫
∫
∫
u
d
x
v\int u\,dx,v''\int\int\int u\,dx
v∫udx,v′′∫∫∫udx 图中黑色地方表示负 比如
−
v
′
∫
∫
u
d
x
-v'\int\int u\,dx
−v′∫∫udx 绿色地方表示
(
−
1
)
n
∫
(
v
n
(
∫
)
n
u
)
d
x
(-1)^n\int (v^n(\int)^nu)dx
(−1)n∫(vn(∫)nu)dx 注意:这里的n表示求导或积分的总次数 最后把这三部分加起来即可,不理解的话请看下面这个例子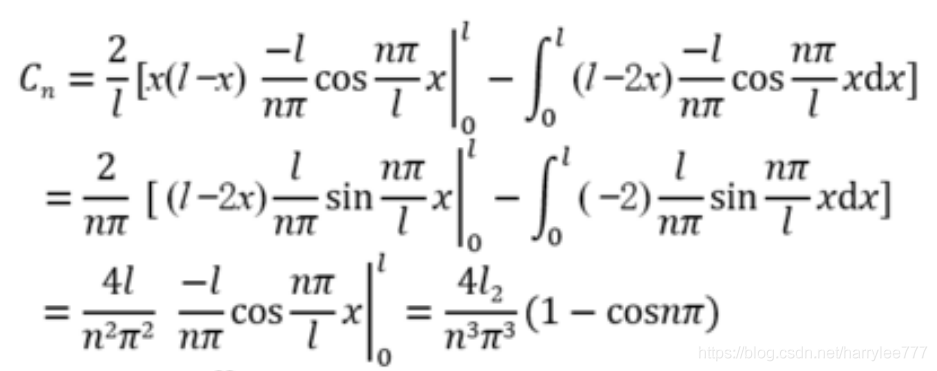 表格法:
表格法: