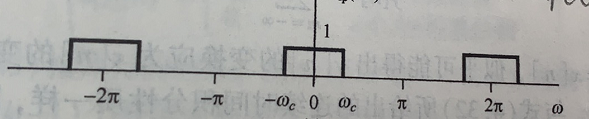方波与sinc函数之间的最全傅里叶变换关系 |
您所在的位置:网站首页 › 傅里叶变换的性质推导 › 方波与sinc函数之间的最全傅里叶变换关系 |
方波与sinc函数之间的最全傅里叶变换关系
|
方波与sinc函数的最全傅里叶变换对_助记_有图有推导
文章目录
方波与sinc函数的最全傅里叶变换对\_助记\_有图有推导1.连续时间周期信号傅里叶变化下的方波与sinc2.离散时间周期信号傅里叶变换下的方波和sinc2.1时域方波,频域sinc2.2时域sinc,频域方波
3.连续时间傅里叶变换下的方波和sinc3.1时域方波,频域sinc3.2时域sinc,频域方波
4.离散时间傅里叶变换下的方波和sinc4.1时域方波,频域sinc4.2时域sinc,频域方波
5结束语
傅里叶变化是信号分析与处理领域的重要理论基石,其搭建了信号时域和频域之间分析的桥梁。而方波与sinc函数之间的傅里叶变换关系,可以说是每一个学过信号类课程的学生必会的知识。方波与sinc函数不仅在工程领域中有着及其重要的应用,傅里叶变换的相关性质也可在这对函数中得到较好地体现。
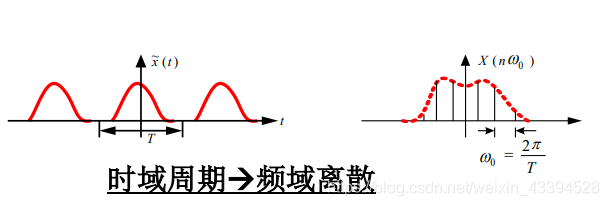
当我们提及方波与sinc函数时,我们可以条件反射般说出:“方波的傅里叶变换时sinc,sinc的傅里叶变换是方波。“但是,由于傅里叶变换存在多种形式(连续的、离散的、周期的、非周期的),当我们具体到特定场景下两者变换的表达式时,我们可能容易搞混。 因而,本篇文章将各种傅里叶变换形式下的方波与sinc函数之间的关系进行整理,并借此分享一下个人的一些助记方法,希望能帮助看到这篇文章的你。 1.连续时间周期信号傅里叶变化下的方波与sinc此类傅里叶变换称为傅里叶级数(FS),信号的时域和频域特性如下: 时域特性:连续,周期信号频域特性:离散,非周期信号其示意图如下: 傅里叶级数变换公式如下: x ( t ) = ∑ n = − ∞ + ∞ X ( n ω 0 ) e j n ω 0 t X ( n ω 0 ) = 1 T ∫ − T / 2 T / 2 x ( t ) e − j n ω 0 t d t 其 中 , ω 0 = 2 π / T x(t)=\sum_{n=-\infty}^{+\infty}{X(n\omega_0)e^{jn\omega_0t}}\\ X(n\omega_0)=\frac{1}{T}\int_{-T/2}^{T/2}x(t)e^{-jn\omega_0t}dt\\ 其中,\omega_0=2\pi/T x(t)=n=−∞∑+∞X(nω0)ejnω0tX(nω0)=T1∫−T/2T/2x(t)e−jnω0tdt其中,ω0=2π/T 在时域为周期连续信号,频域为离散非周期信号的情况下,方波与sinc出现的场景通常是:时域为具有特定占空比的连续周期方波信号,频域为离散的sinc信号。 假定时域周期方波信号的周期为
T
T
T,一个周期内方波的有效长度为
2
T
1
2T_1
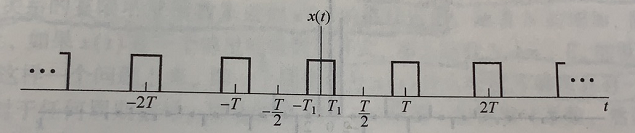
2T1,如下图所示: 其中, ω 0 = 2 π T \omega_0=\frac{2\pi}{T} ω0=T2π 频谱示意图(图片来自《信号与系统》奥本海姆)如下:
对于 X ( 0 ) X(0) X(0),表示信号的0频分量,也即信号的平均值。对于方波信号,平均值即为信号的占空比,所以可以根据周期方波信号的示意图,直接写出 X ( 0 ) X(0) X(0)的值。 对于n不为0的情况,将上述结果进行该写: X ( n ω 0 ) = sin ( n ω 0 T 1 ) n π = ω 0 T 1 sin ( n ω 0 T 1 ) π n ω 0 T 1 = ω 0 T 1 s i n c ( n ω 0 T 1 ) π = 2 π T 1 T s i n c ( n ω 0 T 1 ) π = a 0 s i n c ( n ω 0 T 1 ) X(n\omega_0)=\frac{\sin(n\omega_0T_1)}{n\pi}=\omega_0T_1\frac{\sin(n\omega_0T_1)}{\pi n\omega_0T_1}=\omega_0T_1\frac{sinc(n\omega_0T_1)}{\pi}\\=\frac{2\pi T_1}{T}\frac{sinc(n\omega_0T_1)}{\pi}=a_0sinc(n\omega_0T_1) X(nω0)=nπsin(nω0T1)=ω0T1πnω0T1sin(nω0T1)=ω0T1πsinc(nω0T1)=T2πT1πsinc(nω0T1)=a0sinc(nω0T1) 由上式可知,要确定n不为0时的频谱,需要求的参数 a 0 a_0 a0, ω 0 \omega_0 ω0, T 1 T_1 T1, a 0 a_0 a0即为求得的占空比; ω 0 \omega_0 ω0为基频,当给定周期信号的周期 T T T时, ω 0 \omega_0 ω0便也确定了; T 1 T_1 T1为正半轴第一个零点,根据周期信号的时域示意图,便可以直接得到。 2.离散时间周期信号傅里叶变换下的方波和sinc此类傅里叶变换称为离散傅里叶级数(DFS),信号的时域和频域特性如下: 时域特性:离散,周期信号频域特性:离散,周期信号其示意图如下:
假定时域周期方波信号的周期为 N N N,一个周期内方波的有效长度为 2 N 1 + 1 2N_1+1 2N1+1,如下图所示:
X ( k ω 0 ) = 1 N ∑ n = − N 1 N 1 e − j k ( 2 π / N ) n X(k\omega_0)=\frac{1}{N}\sum_{n=-N_1}^{N_1}{e^{-jk(2\pi/N)n}} X(kω0)=N1n=−N1∑N1e−jk(2π/N)n 令 m = n + N 1 m=n+N_1 m=n+N1,则上式变为: X ( k ω 0 ) = 1 N ∑ m = 0 2 N 1 e − j k ( 2 π / N ) ( m − N 1 ) = 1 N e j k ( 2 π / N ) N 1 ∑ m = 0 2 N 1 e − j k ( 2 π / N ) m = 1 N e j k ( 2 π / N ) N 1 ( 1 − e − j k 2 π ( 2 N 1 + 1 ) / N 1 − e − j k ( 2 π / N ) ) = 1 N sin ( 2 π k ( N 1 + 1 / 2 ) / N ) sin ( π k / N ) X(k\omega_0)=\frac{1}{N}\sum_{m=0}^{2N_1}{e^{-jk(2\pi/N)(m-N_1)}}=\frac{1}{N}e^{jk(2\pi/N)N_1}\sum_{m=0}^{2N_1}{e^{-jk(2\pi/N)m}}\\ =\frac{1}{N}e^{jk(2\pi/N)N_1}(\frac{1-e^{-jk2\pi(2N_1+1)/N}}{1-e^{-jk(2\pi/N)}}) =\frac{1}{N}\frac{\sin(2\pi k(N_1+1/2)/N)}{\sin(\pi k/N)} X(kω0)=N1m=0∑2N1e−jk(2π/N)(m−N1)=N1ejk(2π/N)N1m=0∑2N1e−jk(2π/N)m=N1ejk(2π/N)N1(1−e−jk(2π/N)1−e−jk2π(2N1+1)/N)=N1sin(πk/N)sin(2πk(N1+1/2)/N) 当 k = 0 , ± N , ± 2 N , ⋯ k=0,\pm N,\pm 2N,\cdots k=0,±N,±2N,⋯时,借助洛必达法则得: X ( k ω 0 ) = lim k → 0 1 N sin ( 2 π k ( N 1 + 1 / 2 ) / N ) sin ( π k / N ) = 1 N 2 π ( N 1 + 1 / 2 ) / N cos ( 2 π k ( N 1 + 1 / 2 ) / N ) π / N cos ( π k / N ) = 2 N 1 + 1 N , k = 0 , ± N , ± 2 N , ⋯ X(k\omega_0)=\lim_{k\rightarrow 0} \frac{1}{N}\frac{\sin(2\pi k(N_1+1/2)/N)}{\sin(\pi k/N)}=\frac{1}{N}\frac{2\pi (N_1+1/2)/N\cos(2\pi k(N_1+1/2)/N)}{\pi /N\cos(\pi k/N)}\\ =\frac{2N_1+1}{N},k=0,\pm N,\pm 2N,\cdots X(kω0)=k→0limN1sin(πk/N)sin(2πk(N1+1/2)/N)=N1π/Ncos(πk/N)2π(N1+1/2)/Ncos(2πk(N1+1/2)/N)=N2N1+1,k=0,±N,±2N,⋯ 频谱示意图(图片来自《信号与系统》奥本海姆)如下: 当 k = 0 , ± N , ± 2 N , ⋯ k=0,\pm N,\pm 2N,\cdots k=0,±N,±2N,⋯时,此时的 X ( k ω 0 ) X(k\omega_0) X(kω0),表示信号的平均值,即方波信号的占空比,所以可以根据周期方波信号的示意图,直接写出此时 X ( k ω 0 ) X(k\omega_0) X(kω0)的值。 当 k ≠ 0 , ± N , ± 2 N , ⋯ k\neq0,\pm N,\pm 2N,\cdots k=0,±N,±2N,⋯,可将此时的 1 N sin ( 2 π k ( N 1 + 1 / 2 ) / N ) sin ( π k / N ) \frac{1}{N}\frac{\sin(2\pi k(N_1+1/2)/N)}{\sin(\pi k/N)} N1sin(πk/N)sin(2πk(N1+1/2)/N)与连续周期方波的傅里叶级数 sin ( n ω 0 T 1 ) n π \frac{\sin(n\omega_0T_1)}{n\pi} nπsin(nω0T1)( = 1 N sin ( 2 π n T 1 / N ) n π / N =\frac{1}{N}\frac{\sin(2\pi nT_1/N)}{n\pi /N} =N1nπ/Nsin(2πnT1/N))进行类比: 1)一方面,离散情况下的 N 1 + 1 / 2 N_1+1/2 N1+1/2等价于连续情况的 T 1 T_1 T1 2)另一方面,离散情况下最终结果的分母是一个sin()函数,而连续情况下是一个线性函数。这是因为连续情况下对幂函数 e m x e^{mx} emx进行积分时,在凑积分时,配出来的系数为 1 / m 1/m 1/m;而在离散情况下,对幂函数 e m n e^{mn} emn进行求和时,配出来的系数为 1 / 1 − e m 1/1-e^m 1/1−em,再利用欧拉公式,便可得到 1 / s i n ( ) 1/sin() 1/sin()的形式。 2.2时域sinc,频域方波假定信号的频域为周期方波,周期为 N N N,一个周期内方波的有效长度为 2 N 1 2N_1 2N1.由于傅里叶正变换与逆变换具有很好的对称性,因而此类情景的求解过程与上述过程非常相似,求解过程如下: 选定积分区间 [ − N 1 , N 1 ] [-N_1,N_1] [−N1,N1]来进行计算。利用DTFT的逆变换进行计算 x [ n ] = ∑ k = − N 1 N 1 e j k ( 2 π / N ) n x[n]=\sum_{k=-N_1}^{N_1}{e^{jk(2\pi/N)n}} x[n]=k=−N1∑N1ejk(2π/N)n 令 m = k + N 1 m=k+N_1 m=k+N1,则上式变为: X ( k ω 0 ) = ∑ m = 0 2 N 1 e j n ( 2 π / N ) ( m − N 1 ) = e − j n ( 2 π / N ) N 1 ∑ m = 0 2 N 1 e j n ( 2 π / N ) m = e − j n ( 2 π / N ) N 1 ( 1 − e j n 2 π ( 2 N 1 + 1 ) / N 1 − e j n ( 2 π / N ) ) = sin ( 2 π n ( N 1 + 1 / 2 ) / N ) sin ( π n / N ) , k ≠ 0 , ± N , ± 2 N , ⋯ X(k\omega_0)=\sum_{m=0}^{2N_1}{e^{jn(2\pi/N)(m-N_1)}}=e^{-jn(2\pi/N)N_1}\sum_{m=0}^{2N_1}{e^{jn(2\pi/N)m}}\\ =e^{-jn(2\pi/N)N_1}(\frac{1-e^{jn2\pi(2N_1+1)/N}}{1-e^{jn(2\pi/N)}}) =\frac{\sin(2\pi n(N_1+1/2)/N)}{\sin(\pi n/N)},k\neq0,\pm N,\pm 2N,\cdots X(kω0)=m=0∑2N1ejn(2π/N)(m−N1)=e−jn(2π/N)N1m=0∑2N1ejn(2π/N)m=e−jn(2π/N)N1(1−ejn(2π/N)1−ejn2π(2N1+1)/N)=sin(πn/N)sin(2πn(N1+1/2)/N),k=0,±N,±2N,⋯ 当 k = 0 , ± N , ± 2 N , ⋯ k=0,\pm N,\pm 2N,\cdots k=0,±N,±2N,⋯时,借助洛必达法则得: X ( k ω 0 ) = lim k → 0 sin ( 2 π k ( N 1 + 1 / 2 ) / N ) sin ( π k / N ) = 2 π ( N 1 + 1 / 2 ) / N cos ( 2 π k ( N 1 + 1 / 2 ) / N ) π / N cos ( π k / N ) = 2 N 1 + 1 , k = 0 , ± N , ± 2 N , ⋯ X(k\omega_0)=\lim_{k\rightarrow 0} \frac{\sin(2\pi k(N_1+1/2)/N)}{\sin(\pi k/N)}=\frac{2\pi (N_1+1/2)/N\cos(2\pi k(N_1+1/2)/N)}{\pi /N\cos(\pi k/N)}\\ =2N_1+1,k=0,\pm N,\pm 2N,\cdots X(kω0)=k→0limsin(πk/N)sin(2πk(N1+1/2)/N)=π/Ncos(πk/N)2π(N1+1/2)/Ncos(2πk(N1+1/2)/N)=2N1+1,k=0,±N,±2N,⋯ 助记: 上述运算结果与2.1中的计算结果非常相似,只需去掉2.1中的系数 1 / N 1/N 1/N,并把 k k k换成 n n n,便可得到上述结果 3.连续时间傅里叶变换下的方波和sinc此类傅里叶变换称为傅里叶变化(FT),信号的时域和频域特性如下: 时域特性:连续,非周期信号频域特性:连续,非周期信号其示意图如下: 傅里叶变换公式如下: x ( t ) = 1 2 π ∫ − ∞ + ∞ X ( ω ) e j ω t d ω X ( ω ) = ∫ − ∞ + ∞ x ( t ) e − j ω t d t x(t)=\frac{1}{2\pi}\int_{- \infty}^{+\infty} {X(\omega)e^{j\omega t}d\omega}\\ X(\omega)=\int_{- \infty}^{+\infty} {x(t)e^{-j\omega t}dt} x(t)=2π1∫−∞+∞X(ω)ejωtdωX(ω)=∫−∞+∞x(t)e−jωtdt 注:本文在分析时,默认信号的频率坐标为角频率 ω \omega ω 与周期信号的傅里叶变换相比,FT表示的是更一般的情况,通常有如下两种场景:时域为方波信号,频域为sinc信号以及频域为方波,时域为sinc信号。 3.1时域方波,频域sinc此类情况下,也可分成两种情况:时域为单个方波和时域为周期方波。对于后者,他与前文介绍的FS是同一种情景,只不过这里要求的是周期方波的FT,而不是FS。根据FS与FT之间的关系,可以借助前文求得的傅里叶级数,快速得到时域周期方波的傅里叶变换,两种关系如下:
X
(
ω
)
=
2
π
∑
k
=
−
∞
+
∞
a
k
δ
(
ω
−
k
ω
0
)
,
其
中
ω
0
=
2
π
T
X(\omega)=2\pi\sum_{k=-\infty}^{+\infty}{a_k\delta(\omega-k\omega_0)},其中\omega_0=\frac{2\pi}{T}
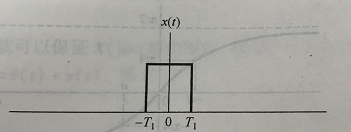
X(ω)=2πk=−∞∑+∞akδ(ω−kω0),其中ω0=T2π 因而,本文主要讨论时域为单个方波的情况。假定时域方波信号的有效长度为
2
T
1
2T_1
2T1,如下图所示:
X
(
ω
)
=
∫
−
T
1
+
T
1
e
−
j
ω
t
d
t
=
2
T
1
s
i
n
(
T
1
ω
)
T
1
ω
=
2
T
1
s
i
n
c
(
T
1
ω
)
X(\omega)=\int_{- T_1}^{+T_1} {e^{-j\omega t}dt}=2T_1\frac{sin(T_1\omega)}{T_1\omega}=2T_1sinc(T_1\omega)
X(ω)=∫−T1+T1e−jωtdt=2T1T1ωsin(T1ω)=2T1sinc(T1ω) 频谱示意图(图片来自《信号与系统》奥本海姆)如下: 助记: 由上述计算结果可知,欲确定方波信号的频谱,仅需要知道参数 T 1 T_1 T1即可(默认方波的幅值为1的前提下)。 参数 T 1 T_1 T1由两部分来共同组成最终结果: 1)常数项系数 2 T 1 2T_1 2T1,本质上表示的是方波信号的面积 2) s i n c ( T 1 ω ) sinc(T_1\omega) sinc(T1ω)项,直接将正半轴的零点当成 ω \omega ω的系数即可 当在具体求解问题时,假如给定一个像上图所示的对称分布的时域方波,再求频域表达式时: 1)先找到正半轴零点 x 0 x_0 x0,这时便可写出sinc项 s i n c ( x 0 ω ) sinc(x_0\omega) sinc(x0ω) 2)再计算出方波的面试 S S S,由此便得到信号频谱: X ( ω ) = S s i n c ( x 0 ω ) X(\omega)=Ssinc(x_0\omega) X(ω)=Ssinc(x0ω) 3.2时域sinc,频域方波假定频域方波信号的有效长度为
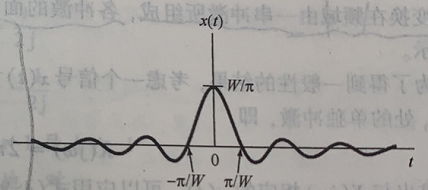
2
W
2W
2W,如下图所示: 利用FT逆变换进行计算,得到信号的时域表达式: x ( t ) = 1 2 π ∫ − W + W e j ω t d ω = 2 W 2 π s i n ( W t ) W t = 2 W 2 π s i n c ( W t ) x(t)=\frac{1}{2\pi}\int_{- W}^{+W} {e^{j\omega t}d\omega}=\frac{2W}{2\pi}\frac{sin(Wt)}{Wt}=\frac{2W}{2\pi}sinc(Wt) x(t)=2π1∫−W+Wejωtdω=2π2WWtsin(Wt)=2π2Wsinc(Wt) 频谱示意图(图片来自《信号与系统》奥本海姆)如下:
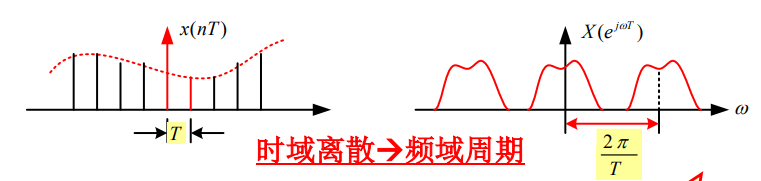
注:上式故意没有进行约分化简,是因为这种形式更具备可解释性,也更方便记忆。 助记: 与时域方波的计算结果类似,仅需将3.1节中的 ω \omega ω替换成 t t t,令外加一个系数 1 / 2 π 1/2\pi 1/2π,便可得到上述结果。欲确定方波信号的时域表达式,仅需要知道参数 W W W即可。 参数 W W W由两部分来共同组成最终结果: 1)常数项系数 2 W / 2 π 2W/2\pi 2W/2π,本质上表示的是方波信号的面积 2) s i n c ( W t ) sinc(Wt) sinc(Wt)项,直接将正半轴的零点当成 t t t的系数即可 当在具体求解问题时,假如给定一个像上图所示的对称分布的频域方波,再求时域表达式时: 1)先找到正半轴零点 W 0 W_0 W0,这时便可写出sinc项 s i n c ( W 0 t ) sinc(W_0t) sinc(W0t) 2)再计算出方波的面试 S S S,由此便得到信号频谱: X ( ω ) = S 2 π s i n c ( x 0 ω ) X(\omega)=\frac{S}{2\pi} sinc(x_0\omega) X(ω)=2πSsinc(x0ω) 将第2节中离散傅里叶级数的两种情况,与本节中的两种情况进行对比可知,前者的两种情况相差一个系数 1 / N 1/N 1/N,后者的两种情况相差一个系数 1 / 2 π 1/2\pi 1/2π;这与DFS与FS正反变换的系数相对应。 4.离散时间傅里叶变换下的方波和sinc此类傅里叶变换称为离散时间傅里叶变化(DTFT),信号的时域和频域特性如下: 时域特性:离散,非周期信号频域特性:连续,周期信号其示意图如下:
与FT类似,DTFT表示的是离散情况下一般的情况,通常有如下两种场景:时域为方波信号,频域为sinc信号以及频域为方波,时域为sinc信号。 4.1时域方波,频域sinc此类情况下,也可分成两种情况:时域为单个方波和时域为周期方波。对于后者,他与前文介绍的DFS是同一种情景,只不过这里要求的是周期方波的DTFT,而不是DFS。根据DFS与DTFT之间的关系,可以借助前文求得的傅里叶级数,快速得到时域周期方波的傅里叶变换,两种关系如下:
X
(
e
j
ω
)
=
2
π
∑
k
=
−
∞
+
∞
a
k
δ
(
ω
−
k
ω
0
)
,
其
中
ω
0
=
2
π
N
X(e^{j\omega})=2\pi\sum_{k=-\infty}^{+\infty}{a_k\delta(\omega-k\omega_0)},其中\omega_0=\frac{2\pi}{N}
X(ejω)=2πk=−∞∑+∞akδ(ω−kω0),其中ω0=N2π 因而,本文主要讨论时域为单个方波的情况。假定时域方波信号的有效长度为
2
N
1
+
1
2N_1+1
2N1+1,如下图所示: 利用DTFT正变换进行计算,得到信号的频谱: X ( e j ω ) = ∑ n − N 1 + N 1 e − j ω n = s i n ( ( N 1 + 1 ) ω ) s i n ( w / 2 ) X(e^{j\omega})=\sum_{n- N_1}^{+N_1} {e^{-j\omega n}}=\frac{sin((N_1+1)\omega)}{sin(w/2)} X(ejω)=n−N1∑+N1e−jωn=sin(w/2)sin((N1+1)ω) 频谱示意图(图片来自《信号与系统》奥本海姆)如下:
由上述计算结果可知,欲确定方波信号的频谱,仅需要知道参数 N 1 N_1 N1即可(默认方波的幅度为1的前提下)。 可以将此结果 s i n ( ( N 1 + 1 ) ω ) s i n ( w / 2 ) \frac{sin((N_1+1)\omega)}{sin(w/2)} sin(w/2)sin((N1+1)ω)与4.1连续方波信号的频谱表达式 2 T 1 s i n c ( T 1 ω ) 2T_1sinc(T_1\omega) 2T1sinc(T1ω)( = 2 T 1 s i n ( T 1 ω ) T 1 ω = s i n ( T 1 ω ) ω / 2 =2T_1\frac{sin(T_1\omega)}{T_1\omega}=\frac{sin(T_1\omega)}{\omega/2} =2T1T1ωsin(T1ω)=ω/2sin(T1ω))进行对比记忆。 4.2时域sinc,频域方波假定在一个周期内频域方波信号的有效长度为 2 ω c 2\omega_c 2ωc,如下图所示:
利用DTFT逆变换进行计算,得到信号的时域表达式: x [ n ] = 1 2 π ∫ 2 π e j ω n d ω = 2 ω c 2 π s i n ( ω c n ) ω c n = 2 ω c 2 π s i n c ( ω c n ) x[n]=\frac{1}{2\pi}\int_{2\pi} {e^{j\omega n}d\omega}=\frac{2\omega_c}{2\pi}\frac{sin(\omega_cn)}{\omega_cn}=\frac{2\omega_c}{2\pi}sinc(\omega_cn) x[n]=2π1∫2πejωndω=2π2ωcωcnsin(ωcn)=2π2ωcsinc(ωcn) 助记: 上述计算结果与3.2节频域为单个方波的情况非常相似,这是因为两者都是连续谱,尽管本节涉及到的频谱是周期谱,但是积分区间仅在 2 π 2\pi 2π范围内,这和3.2节整个 ω \omega ω轴上的积分没有区别。 因而,仿照3.2节的计算方式,直接便可以写出本节的结果。 5结束语以上便是信号分量与处理领域,所涉及到的几乎全部场景下的方波与sinc变换对的具体形式,希望能够对正在学习相关课程的同学,以及学过相关课程但是有所遗忘的同学有所帮助。 最后,需要说明的是,以上内容大部分是自己总结的一些‘规律’,其主要出发点是希望能够将各个知识点串联起来,有个宏观的把握,从而有利于记忆。如果内容中存在错误的话,非常欢迎在评论区或私信我进行指正,谢谢。 另外,整理不易,如果觉得对你有所帮助的话,希望能帮忙点个赞,谢谢~ 此外,转载请注明出处。 |
【本文地址】
今日新闻 |
推荐新闻 |

 选定积分区间[-T/2,T/2]来进行计算,需要注意的时,在计算时,要分n是否为0进行讨论,因为在计算积分的过程中,会出现1/n这一项,因而需要讨论n是否为0. 当n为0时:
X
(
0
ω
0
)
=
1
T
∫
−
T
1
T
1
d
t
=
2
T
1
T
X(0\omega_0)=\frac{1}{T}\int_{-T_1}^{T_1}dt=\frac{2T_1}{T}
X(0ω0)=T1∫−T1T1dt=T2T1 当n不为0时:
X
(
n
ω
0
)
=
1
T
∫
−
T
1
T
1
e
−
j
n
ω
0
t
d
t
=
−
1
j
n
ω
0
T
e
−
j
n
ω
0
t
∣
−
T
1
T
1
=
sin
(
n
ω
0
T
1
)
n
π
X(n\omega_0)=\frac{1}{T}\int_{-T_1}^{T_1}{e^{-jn\omega_0t}}dt=-\frac{1}{jn\omega_0T}e^{-jn\omega_0t}|_{-T_1}^{T_1}\\ =\frac{\sin(n\omega_0T_1)}{n\pi}
X(nω0)=T1∫−T1T1e−jnω0tdt=−jnω0T1e−jnω0t∣−T1T1=nπsin(nω0T1)
选定积分区间[-T/2,T/2]来进行计算,需要注意的时,在计算时,要分n是否为0进行讨论,因为在计算积分的过程中,会出现1/n这一项,因而需要讨论n是否为0. 当n为0时:
X
(
0
ω
0
)
=
1
T
∫
−
T
1
T
1
d
t
=
2
T
1
T
X(0\omega_0)=\frac{1}{T}\int_{-T_1}^{T_1}dt=\frac{2T_1}{T}
X(0ω0)=T1∫−T1T1dt=T2T1 当n不为0时:
X
(
n
ω
0
)
=
1
T
∫
−
T
1
T
1
e
−
j
n
ω
0
t
d
t
=
−
1
j
n
ω
0
T
e
−
j
n
ω
0
t
∣
−
T
1
T
1
=
sin
(
n
ω
0
T
1
)
n
π
X(n\omega_0)=\frac{1}{T}\int_{-T_1}^{T_1}{e^{-jn\omega_0t}}dt=-\frac{1}{jn\omega_0T}e^{-jn\omega_0t}|_{-T_1}^{T_1}\\ =\frac{\sin(n\omega_0T_1)}{n\pi}
X(nω0)=T1∫−T1T1e−jnω0tdt=−jnω0T1e−jnω0t∣−T1T1=nπsin(nω0T1)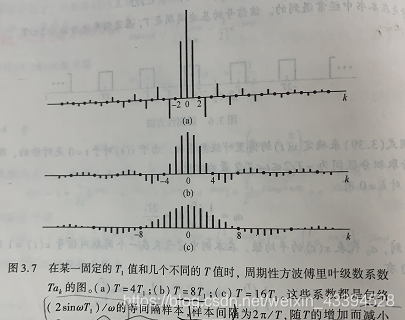 助记:
助记: 离散傅里叶变换公式如下:
x
[
n
]
=
x
(
n
T
1
)
=
∑
k
=
<
N
>
X
(
k
ω
0
)
e
j
k
ω
0
n
=
∑
k
=
<
N
>
X
(
k
ω
0
)
e
j
k
(
2
π
/
N
)
n
X
(
k
ω
0
)
=
1
N
∑
n
=
<
N
>
x
[
n
]
e
−
j
k
ω
0
n
=
1
N
∑
n
=
<
N
>
x
[
n
]
e
−
j
k
(
2
π
/
N
)
n
x[n]=x(nT_1)=\sum_{k=}{X(k\omega_0)e^{jk\omega_0n}}=\sum_{k=}{X(k\omega_0)e^{jk(2\pi /N)n}}\\ X(k\omega_0)=\frac{1}{N}\sum_{n=}{x[n]e^{-jk\omega_0n}}=\frac{1}{N}\sum_{n=}{x[n]e^{-jk(2\pi /N)n}}
x[n]=x(nT1)=k=∑X(kω0)ejkω0n=k=∑X(kω0)ejk(2π/N)nX(kω0)=N1n=∑x[n]e−jkω0n=N1n=∑x[n]e−jk(2π/N)n 由于时域和频域均为周期的离散信号,所以方波与sinc出现的场景具有对称性,通常有如下两种场景:时域为具有特定占空比的离散周期方波信号,频域为离散周期sinc信号以及频域为具有特定占空比的离散周期方波信号,时域为离散周期sinc信号。
离散傅里叶变换公式如下:
x
[
n
]
=
x
(
n
T
1
)
=
∑
k
=
<
N
>
X
(
k
ω
0
)
e
j
k
ω
0
n
=
∑
k
=
<
N
>
X
(
k
ω
0
)
e
j
k
(
2
π
/
N
)
n
X
(
k
ω
0
)
=
1
N
∑
n
=
<
N
>
x
[
n
]
e
−
j
k
ω
0
n
=
1
N
∑
n
=
<
N
>
x
[
n
]
e
−
j
k
(
2
π
/
N
)
n
x[n]=x(nT_1)=\sum_{k=}{X(k\omega_0)e^{jk\omega_0n}}=\sum_{k=}{X(k\omega_0)e^{jk(2\pi /N)n}}\\ X(k\omega_0)=\frac{1}{N}\sum_{n=}{x[n]e^{-jk\omega_0n}}=\frac{1}{N}\sum_{n=}{x[n]e^{-jk(2\pi /N)n}}
x[n]=x(nT1)=k=∑X(kω0)ejkω0n=k=∑X(kω0)ejk(2π/N)nX(kω0)=N1n=∑x[n]e−jkω0n=N1n=∑x[n]e−jk(2π/N)n 由于时域和频域均为周期的离散信号,所以方波与sinc出现的场景具有对称性,通常有如下两种场景:时域为具有特定占空比的离散周期方波信号,频域为离散周期sinc信号以及频域为具有特定占空比的离散周期方波信号,时域为离散周期sinc信号。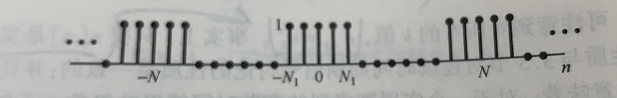 选定积分区间
[
−
N
1
,
N
1
]
[-N_1,N_1]
[−N1,N1]来进行计算。与上述连续周期方波的求解不同,在计算时,不需要讨论k是否为0,但要注意DFS的周期性.
选定积分区间
[
−
N
1
,
N
1
]
[-N_1,N_1]
[−N1,N1]来进行计算。与上述连续周期方波的求解不同,在计算时,不需要讨论k是否为0,但要注意DFS的周期性. 助记:
助记:
 利用FT正变换进行计算,得到信号的频谱:
利用FT正变换进行计算,得到信号的频谱:

 离散时间傅里叶变换公式如下:
x
[
n
]
=
x
(
n
t
)
=
1
2
π
∫
2
π
X
(
e
j
ω
)
e
j
ω
n
d
ω
X
(
e
j
ω
)
=
∑
n
=
−
∞
+
∞
x
(
n
)
e
−
j
ω
n
x[n]=x(nt)=\frac{1}{2\pi}\int_{2\pi} {X(e^{j\omega})e^{j\omega n}d\omega}\\ X(e^{j\omega})=\sum_{n=- \infty}^{+\infty} {x(n)e^{-j\omega n}}
x[n]=x(nt)=2π1∫2πX(ejω)ejωndωX(ejω)=n=−∞∑+∞x(n)e−jωn 注:本文在分析时,默认信号的频率坐标为角频率
ω
\omega
ω
离散时间傅里叶变换公式如下:
x
[
n
]
=
x
(
n
t
)
=
1
2
π
∫
2
π
X
(
e
j
ω
)
e
j
ω
n
d
ω
X
(
e
j
ω
)
=
∑
n
=
−
∞
+
∞
x
(
n
)
e
−
j
ω
n
x[n]=x(nt)=\frac{1}{2\pi}\int_{2\pi} {X(e^{j\omega})e^{j\omega n}d\omega}\\ X(e^{j\omega})=\sum_{n=- \infty}^{+\infty} {x(n)e^{-j\omega n}}
x[n]=x(nt)=2π1∫2πX(ejω)ejωndωX(ejω)=n=−∞∑+∞x(n)e−jωn 注:本文在分析时,默认信号的频率坐标为角频率
ω
\omega
ω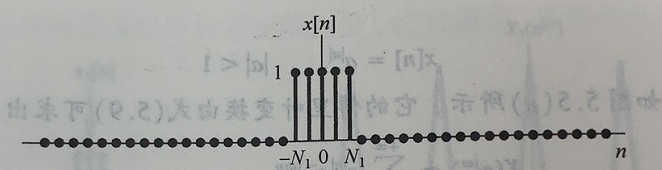
 助记:
助记: