自控理论 第6章 II 相对稳定性、伯德图和闭环频率响应 |
您所在的位置:网站首页 › 伯德图穿越频率与转折频率区别 › 自控理论 第6章 II 相对稳定性、伯德图和闭环频率响应 |
自控理论 第6章 II 相对稳定性、伯德图和闭环频率响应
|
6.4 相对稳定性分析
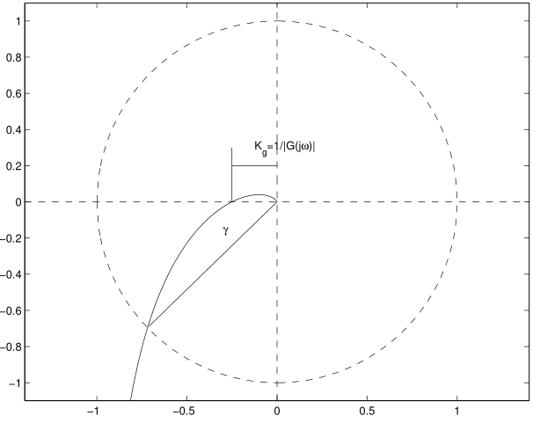
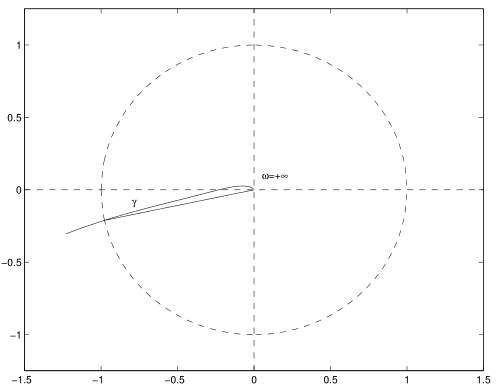
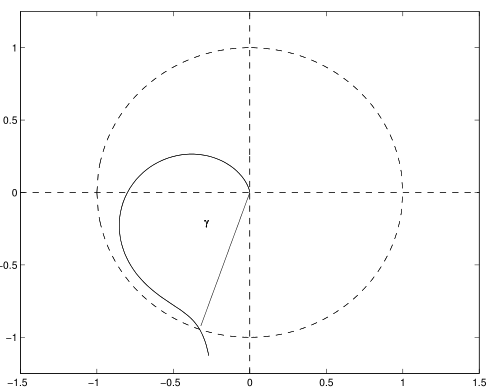
前边的讨论大多局限于稳定或不稳定,现在讨论如果稳定,能有多稳定。这在实际中是很需要的,毕竟实际中充满了干扰。 6.4.1 使用保角变换分析相对稳定性等我之后复习(预习)一下复变函数再过来补这一节吧。。。 6.4.2 \(\mathcal H_\infty\)控制健壮(robust)控制(实在不想用“鲁棒”这种莫名其妙的翻译💢)相关,不会先留着。。。 6.4.3 幅值裕度和相位裕度 定义幅值裕度 定义相位交越频率\(\omega_1\in(0,\infty)\),其满足\(\angle G_o(j\omega_1)=-\pi\),则幅值裕度为 \[K_g=\frac{1}{|G_o(j\omega_1)|} \]使用分贝表示则是(用的多) \[K_g\mathrm{dB}=20\log K_g=-20\log |G_o(j\omega_1)| \]当讨论幅值裕度的正负时,讨论的就是用分贝表示的,容易知道,当\(|G_o(j\omega_1)|\ge1\)时,\(K_g\mathrm{dB}\le0\),反之则\(K_g\mathrm{dB}>0\)。 假如奈奎斯特曲线来回穿越实轴,也即是有多个\(\omega\)满足\(\angle G_o(j\omega)=-\pi\),这时候幅值裕度该取哪一个点来计算? 课上没有提但是有个题涉及到了,我自己感觉如果稳定当前系统稳定,该取\((-1,j0)\)左侧最近的点;如果不稳定,该取右侧最近的点。 相位裕度 定义幅值交越频率\(\omega_2\in(0,\infty)\),其满足\(|G(j\omega_2)|=1\),则相位裕度为 \[\gamma=\pi+\angle G(j\omega_2) \]幅值裕度和相位裕度单独使用不能描述系统的相对稳定性,合在一块才可以。 最小相位系统裕度的图形意义一个幅值裕度和相位裕度都很大的系统,比较稳定
一个幅值裕度很大但是相位裕度很小的系统,对相角的扰动很可能使系统不稳定
一个幅值裕度很小但是相位裕度很大的系统,对幅值的扰动很可能使系统不稳定
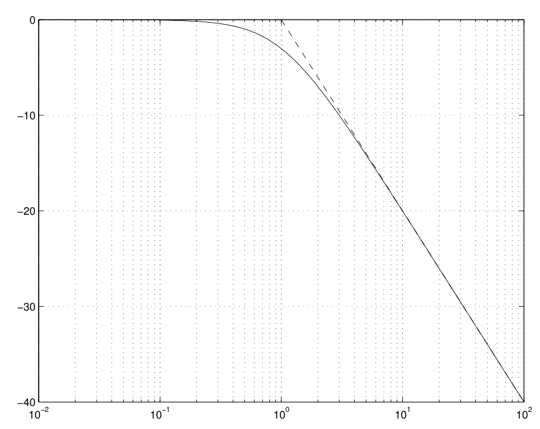
上述几幅图说明,对于最小相位系统,只有幅值裕度和相位裕度都大于0系统才能稳定。 注意,该结论只对最小相位系统成立。 6.5 伯德图奈奎斯特图中频率没有得到定量体现,伯德图在这方面可以作为补充。 6.5.1 引入 使用对数的原因 横坐标\(\omega\):系统需要考虑的频率很宽有可能从及赫兹(机械结构)到几兆赫兹(电子系统) 纵坐标\(|G(j\omega)|\):系统经常需要作出修正,对数将乘法化为加法看起来更直观。 定义:对数化的频率响应曲线即是伯德图 振幅响应两个轴都取对数 幅角相应只有横轴取对数 6.5.2 常用环节的伯德图 常数环节表达式如下 \[G(j\omega)=K_m\\ \Rightarrow \left\{ \begin{aligned} 20\log\left|G(j\omega)\right|&=20\log K_m\\ \angle G(j\omega)&=0 \end{aligned} \right. \]微/积分环节表达式如下 \[G(j\omega)=(j\omega)^{\pm1}\\ \Rightarrow \left\{ \begin{aligned} 20\log\left|G(j\omega)\right|&=\pm20\log\omega\\ \angle G(j\omega)&=\pm \frac{\pi}{2} \end{aligned} \right.\\ \]一阶微分/惯性环节表达式 \[G(j\omega)=(1+j\omega T)^{\pm1}\\ \Rightarrow \left\{ \begin{aligned} 20\log\left|G(j\omega)\right|&=\pm20\log\sqrt{1+(\omega T)^2}\\ \angle G(j\omega)&=\pm\arctan(\omega T) \end{aligned} \right.\\ \]渐近线 可以通过\(\omega T\)与\(1\)的大小关系作伯德图的渐近线,以\(\frac{1}{1+j\omega T}\)为例(下边的讨论也是一样,毕竟一阶惯性环节见得多): \[-20\log\sqrt{1+(\omega T)^2}\mathrm{dB}\approx \mathrm{Asym(\left|G(j\omega\right|)}= \left\{ \begin{aligned} &0\ & for\ \omega T\ll 1\\ &-20\log\omega T\ & for\ \omega T\gg1 \end{aligned} \right. \]\(\mathrm{Asym}\)指渐近线asymptote。
横轴是\(\omega T\)。 渐近线的误差 渐近线与完整的幅值响应之间的误差由上图很明显在中间(\(\omega=1\))时最大,在两头则很小,可以具体计算一下: \[\begin{aligned} \mathrm{Err}(\omega)&=20 \log |G(j \omega)|-\operatorname{Asym}(|G(j \omega)|) \\ &= \begin{cases}-20 \log \sqrt{1+(\omega T)^{2}} & 0 |
【本文地址】