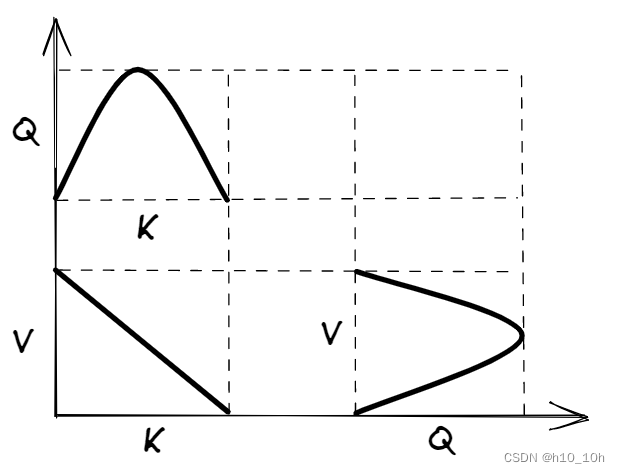
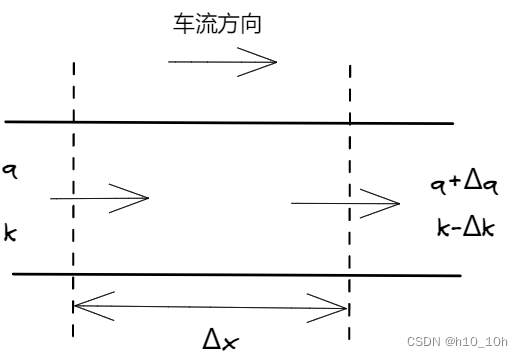
由流率 Q Q Q、行车速度 V s ‾ \overline{V_s} Vs​​、密度 K K K三个基本参数之间的关系 Q = V s ‾ K (1) Q=\overline{V_s}K\tag{1} Q=Vs​​K(1) 和速度-密度之间的线性关系（格林-希尔兹Greenshields）： V = V f ( 1 − K K j ) (2) V=V_f(1-\frac{K}{K_j})\tag{2} V=Vf​(1−Kj​K​)(2) ^f56ffb

当交通密度很大时，可以采用格林伯(Grenberg)提出的对数模型： V = V m l n K j K V=V_mln\frac{K_j}{K} V=Vm​lnKKj​​，对数模型保证随着密度 K K K趋近 K j K_j Kj​， V V V趋近0 当交通密度很小时，可采用Underwood提出的指数模型： V = V f e − K K m V=V_f e^{-\frac {K}{K_m}} V=Vf​e−Km​K​，指数模型保证随着密度 K K K趋近0， V V V趋近 V f V_f Vf​ ^894ef9

由公式[[03交通流理论#^f56ffb|(1)(2)]]可以推导得出： 流率与密度的关系 Q = K V f ( 1 − K K j ) (3) Q=KV_f(1-\frac{K}{K_j})\tag{3} Q=KVf​(1−Kj​K​)(3) 流率与速度关系 K = K j ( 1 − V V f ) K=K_j(1-\frac{V}{V_f}) K=Kj​(1−Vf​V​) Q = K j V ( 1 − V V f ) (4) Q=K_jV(1-\frac{V}{V_f})\tag{4} Q=Kj​V(1−Vf​V​)(4) K j K_j Kj​：K_jam，拥挤密度 V f V_f Vf​：V_free，自由流速 V m V_m Vm​：临界速度 K m K_m Km​：最佳密度

随着车流密度增大，行车速度线性下降。 交通流率与车流密度呈抛物线关系。 交通流率与行车速度呈抛物线关系。随着车速降低，流率先增大后减小。

密度等值图的体积是该道路上所有车辆的总行程时间。

车辆通过交叉口时，车队中前几辆车的车头时距需要考虑到司机看到绿灯的反应时间和车辆启动加速时间，故相对较大。车辆启动造成的影响随着后续车辆的到来逐渐减弱，直到车辆在穿过停车线的时候已经完全加速。车头时距趋于稳定，称为饱和车头时距 h h h。

前几辆车的超时（即消耗的大于饱和车头时距 h h h的时间）加在一起，称为[[信号参数与配时参数|启动损失时间]] l 1 l_1 l1​。

跟驰理论研究在无法超车的单一车道上车辆队列行驶时，后车跟随前车（非自由状态）的行驶状态的一种理论。

驾驶员在驾驶车辆跟驰的过程中，自身加速度与自身车速及前后车速度差成正比，与前后车间距成反比 a n ( t ) = c [ v n ( t ) ] m v n − 1 ( t − T ) − v n ( t − T ) [ x n − 1 ( t − T ) − x n ( t − T ) ] l a_n(t)=c[v_n(t)]^m\frac{v_{n-1}(t-T)-v_n(t-T)}{[x_{n-1}(t-T)-x_n(t-T)]^l} an​(t)=c[vn​(t)]m[xn−1​(t−T)−xn​(t−T)]lvn−1​(t−T)−vn​(t−T)​

GM模型能够建立起微观跟驰行为与[[03交通流理论#^0e2213|交通流三参数基本图模型]]之间的关系。 当 m = 0 , l = 2 m=0,l=2 m=0,l=2时，可以转换为[[03交通流理论#^f56ffb|Greeshields]]模型 当 m = 0 , l = 1 m=0,l=1 m=0,l=1时，可以转换为[[03交通流理论#^894ef9|Grenberg]]模型 当 m = 1 , l = 2 m=1,l=2 m=1,l=2时，可以转换为Underwood模型

GM模型的缺陷： 当前后两车速度相等时，无论前后车之间的跟车距离如何不实际，后车都将维持现状而不产生加速度。 当后车在驾驶过程中被迫停止后，由于速度为零，其加速度也为零，车辆无法再启动。

Komentani和Sasaki：假设驾驶员在不能完全预判前车运动的情况下，必须保持合理的间距以免碰撞 前后车之间距离是前车速度和后车速度的函数 Δ x n ( t − T ) = α v n − 1 2 ( t − T ) + β n v n 2 ( t ) + β v n ( t ) + b 0 \Delta x_n(t-T)=\alpha v_{n-1}^2(t-T)+\beta_n v_n^2(t)+\beta v_n(t)+b_0 Δxn​(t−T)=αvn−12​(t−T)+βn​vn2​(t)+βvn​(t)+b0​

Gipps：同时考虑自由驾驶状态和跟驰状态，其中跟驰状态的基本假设是前车速度突然减速，后车必须保持足够的安全间距以供紧急制动避免碰撞

Newell：对于不同的跟驰距离，驾驶者存在着与之对应的期望速度，并试图通过一个时间 τ \tau τ，将车速调整至期望的速度

全速度差模型FVDM：既考虑当前车速与期望速度的差异，又考虑自身车速与前车速度的差异。在模拟实际跟驰行为时效果较好。 a n ( t ) = α [ V ( Δ x n ( t ) ) − v n ( t ) ] + λ Δ v n ( t ) a_n(t)=\alpha[V(\Delta x_n(t))-v_n(t)]+\lambda \Delta v_n(t) an​(t)=α[V(Δxn​(t))−vn​(t)]+λΔvn​(t)

Treiber和Helbing认为车辆的加速度可以看作源于驾驶员期望提速的“动力”和前方车辆阻碍形成的“阻力”的综合影响，并基于此构建了智能驾驶员模型(Intelligent Driver Model, IDM)

流体力学模拟理论运用流体力学的基本原理，模拟流体的连续性方程，建立车流的连续性方程。把车流密度的疏密变化比拟成水波的起伏。通过分析车流波的传播速度，寻求车流流率和密度、速度之间的关系。

两种不同密度的分界线在队列中传播的过程称为车流波。车流波传播的速度为波速。（行波）

车流率随距离而降低时，车流密度随时间而增大

∂ k ∂ t + ∂ q ∂ x = 0 (6) \frac {\partial k}{\partial t}+\frac {\partial q}{\partial x}=0\tag{6} ∂t∂k​+∂x∂q​=0(6) ^a3784f

行波就是随着时间会向前推移，振幅不变的波。驻波是两个振幅频率相同传播方向相反的波叠加形成的，不会向前推进。纵波和横波只是指振动方向是沿波的传播方向纵波还是垂直于波的传播方向横波而已。 横波和纵波都可以形成驻波。

交通流中流率 q q q和密度 k k k符合基本图关系，且依赖于时间和位置关系 q ( x , t ) = Q ( k ( x , t ) ) (7) q(x,t)=Q(k(x,t))\tag{7} q(x,t)=Q(k(x,t))(7) ^dcab84

将公式[[03交通流理论#dcab84|(7)]]带入公式[[03交通流理论#a3784f|(6)]]，可以得到行波解 x = Q ′ ( k ) t + C 0 x=Q'(k)t+C_0 x=Q′(k)t+C0​ C 0 C_0 C0​：积分常数，根据行波解性质，交通流密度波速 μ = Q ′ ( k ) \mu=Q'(k) μ=Q′(k) 反映在基本图上，波速 v v v为流率 Q Q Q关于密度曲线 k k k的切线斜率

单一密度状态的交通流行波行波解特征线相互平行，两个密度状态相遇时，反应不同密度状态的特征相交，造成密度值发生突变，即产生激波。每条特征线的多个交点中均存在唯一一个真实反映交通状态变化的交点，所有这一交点的集合称为激波路径。

基本公式 P ( k ) = ( λ t ) k e − λ t k ! , k = 0 , 1 , 2 , . . . P(k)=\frac {(\lambda t)^ke^{-\lambda t}}{k!},k=0,1,2,... P(k)=k!(λt)ke−λt​,k=0,1,2,...，若令 m = λ t m=\lambda t m=λt为在计数间隔 t t t内平均到达的车辆（人）数，则有 P ( k ) = m k e m k ! P(k)=\frac {m^ke^m}{k!} P(k)=k!mkem​

递推公式 P ( 0 ) = e − m P(0)=e^{-m} P(0)=e−m P ( k + 1 ) = m k + 1 P ( k ) P(k+1)=\frac{m}{k+1}P(k) P(k+1)=k+1m​P(k) E = S = k = λ t E=S=k=λt E=S=k=λt 适用于车流密度低，车辆间相互影响微弱，即车流是随机的

基本公式 P ( k ) = C n k ( λ t n ) k ( 1 − λ t n ) n − k , k = 0 , 1 , 2 , . . . , n P(k)=\mathrm{C}_n^k(\frac {\lambda t}{n})^k(1-\frac {\lambda t}{n})^{n-k},k=0,1,2,...,n P(k)=Cnk​(nλt​)k(1−nλt​)n−k,k=0,1,2,...,n 令 p = λ t / n p=\lambda t/n p=λt/n，则上式为 P ( k ) = C n k p k ( 1 − p ) n − k , k = 0 , 1 , 2 , . . . , n P(k)=\mathrm{C}_n^kp^k(1-p)^{n-k},k=0,1,2,...,n P(k)=Cnk​pk(1−p)n−k,k=0,1,2,...,n

E = n p E=np E=np， S = n p ( 1 − p ) S=np(1-p) S=np(1−p) 适用于车流比较拥挤、自由行驶机会不多的车流用二项分布拟合较好 当观测数据表明 S 2 / m S^2/m S2/m显著大于1.0时就是二项分布不适的表示

基本公式 P ( k ) = C k + β − 1 β − 1 p β ( 1 − p ) k , k = 0 , 1 , 2 , . . . , n P(k)=\mathrm{C}_{k+\beta-1}^{\beta-1}p^{\beta}(1-p)^{k},k=0,1,2,...,n P(k)=Ck+β−1β−1​pβ(1−p)k,k=0,1,2,...,n E = β ( 1 − β ) , D = β ( 1 − p ) / p 2 , M < D E=\beta(1-\beta),D=\beta(1-p)/p^2,M