最优路径算法（python） |
您所在的位置：网站首页 › 代价树的广度优先搜索Python › 最优路径算法（python） |
最优路径算法（python）
|
最优路径算法（python实现）
从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径，称为最短路径 主要的最优（最短）路径算法： 一、深度优先算法；二、广度优先算法；三、Dijstra最短路径；四、floyd最短路径 深度优先算法图的深度优先搜索(Depth First Search)，和树的先序遍历比较类似。 它的思想：假设初始状态是图中所有顶点均未被访问，则从某个顶点v出发，首先访问该顶点，然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。 无向无权值网络
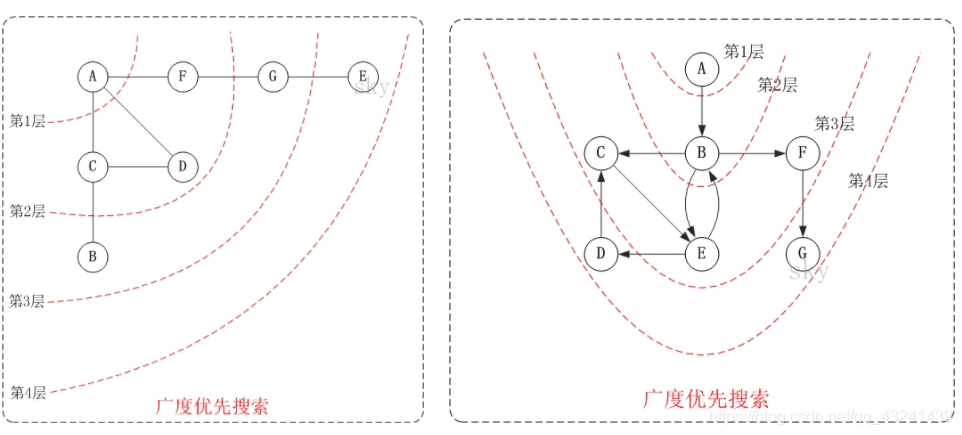
输入（无向图）： data = [[0, 0, 1, 1, 0, 1, 0], [0, 0, 1, 0, 0, 0, 0], [1, 1, 0, 1, 0, 0, 0], [1, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 1], [1, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 1, 1, 0]] 输出： [‘A’, ‘C’, ‘B’, ‘D’, ‘F’, ‘G’, ‘E’] 广度优先算法广度优先搜索算法(Breadth First Search)，又称为"宽度优先搜索"或"横向优先搜索"，简称BFS。 它的思想是：从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起始点，重复上述过程，直至图中所有顶点都被访问到为止。 换句话说，广度优先搜索遍历图的过程是以v为起点，由近至远，依次访问和v有路径相通且路径长度为1,2…的顶点。 输入（有向图）： data_w = [[0, 1, 0, 0, 0, 0, 0], [0, 0, 1, 0, 1, 1, 0], [0, 0, 0, 0, 1, 0, 0], [0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 0, 0]] 输出： [‘A’, ‘B’, ‘C’, ‘E’, ‘F’, ‘D’, ‘G’] Dijstra最短路径（迪杰斯特拉算法）迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。 OSPF协议 ：Open Shortest Path First开放式最短路径优先，底层是迪杰斯特拉算法，是链路状态路由选择协议，它选择路由的度量标准是带宽，延迟。
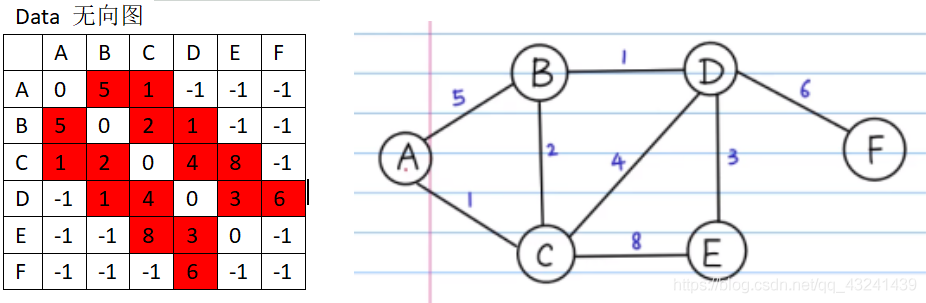
输入： data_weight = [[0, 5, 1, -1, -1, -1], [5, 0, 2, 1, -1, -1], [1, 2, 0, 4, 8, -1], [-1, 1, 4, 0, 3, 6], [-1, -1, 8, 3, 0, -1], [-1, -1, -1, 6, -1, -1]] data_index = [‘A’, ‘B’, ‘C’, ‘D’, ‘E’, ‘F’] d1, d2 = dijkstra_search(data_weight, data_index, 0) 输出： 路径最短距离为： 10 最优路线为： [‘A’, ‘C’, ‘B’, ‘D’, ‘F’] floyd最短路径算法的特点： 弗洛伊德算法是解决任意两点间的最短路径的一种算法，可以正确处理有向图或有向图或负权（但不可存在负权回路)的最短路径问题，同时也被用于计算有向图的传递闭包。 算法的思路： 通过Floyd计算图G=(V,E)中各个顶点的最短路径时，需要引入两个矩阵，矩阵S中的元素a[i][j]表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离。矩阵P中的元素b[i][j]，表示顶点i到顶点j经过了b[i][j]记录的值所表示的顶点。 假设图G中顶点个数为N，则需要对矩阵D和矩阵P进行N次更新。初始时，矩阵D中顶点a[i][j]的距离为顶点i到顶点j的权值；如果i和j不相邻，则a[i][j]=∞，矩阵P的值为顶点b[i][j]的j的值。 接下来开始，对矩阵D进行N次更新。第1次更新时，如果”a[i][j]的距离” > “a[i][0]+a[0][j]”(a[i][0]+a[0][j]表示”i与j之间经过第1个顶点的距离”)，则更新a[i][j]为”a[i][0]+a[0][j]”,更新b[i][j]=b[i][0]。 同理，第k次更新时，如果”a[i][j]的距离” > “a[i][k-1]+a[k-1][j]”，则更新a[i][j]为”a[i][k-1]+a[k-1][j]”,b[i][j]=b[i][k-1]。更新N次之后，操作完成！ Floyd-Warshall算法，简称Floyd算法，用于求解任意两点间的最短距离，时间复杂度为O(n^3)。 使用条件&范围 通常可以在任何图中使用，包括有向图、带负权边的图。 Floyd-Warshall 算法用来找出每对点之间的最短距离。它需要用邻接矩阵来储存边，这个算法通过考虑最佳子路径来得到最佳路径。 1.注意单独一条边的路径也不一定是最佳路径。 2.从任意一条单边路径开始。所有两点之间的距离是边的权，或者无穷大，如果两点之间没有边相连。 对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。 3.不可思议的是，只要按排适当，就能得到结果。 import sys sys.setrecursionlimit(100000000) # 弗洛伊德算法 def floyd(): n = len(graph) for k in range(n): for i in range(n): for j in range(n): if graph[i][k] + graph[k][j] < graph[i][j]: graph[i][j] = graph[i][k] + graph[k][j] parents[i][j] = parents[k][j] # 更新父结点 # 打印路径 def print_path(i, j): if i != j: print_path(i, parents[i][j]) print(j, end='-->') # Data [u, v, cost] datas = [ [0, 1, 2], [0, 2, 6], [0, 3, 4], [1, 2, 3], [2, 0, 7], [2, 3, 1], [3, 0, 5], [3, 2, 12], ] n = 4 # 无穷大 inf = 9999999999 # 构图 graph = [[(lambda x: 0 if x[0] == x[1] else inf)([i, j]) for j in range(n)] for i in range(n)] parents = [[i] * n for i in range(4)] # 关键地方，i-->j 的父结点初始化都为i for u, v, c in datas: graph[u][v] = c floyd() print('Costs:') for row in graph: for e in row: print('∞' if e == inf else e, end='\t') print() print('\nPath:') for i in range(n): for j in range(n): print('Path({}-->{}): '.format(i, j), end='') print_path(i, j) print(' cost:', graph[i][j]) # 最终的graph # graph[i][j]表示i-->j的最短路径 # 0 2 5 4 # 9 0 3 4 # 6 8 0 1 # 5 7 10 0 # # Path: # Path(0-->0): 0--> cost: 0 # Path(0-->1): 0-->1--> cost: 2 # Path(0-->2): 0-->1-->2--> cost: 5 # Path(0-->3): 0-->3--> cost: 4 # Path(1-->0): 1-->2-->3-->0--> cost: 9 # Path(1-->1): 1--> cost: 0 # Path(1-->2): 1-->2--> cost: 3 # Path(1-->3): 1-->2-->3--> cost: 4 # Path(2-->0): 2-->3-->0--> cost: 6 # Path(2-->1): 2-->3-->0-->1--> cost: 8 # Path(2-->2): 2--> cost: 0 # Path(2-->3): 2-->3--> cost: 1 # Path(3-->0): 3-->0--> cost: 5 # Path(3-->1): 3-->0-->1--> cost: 7 # Path(3-->2): 3-->0-->1-->2--> cost: 10 # Path(3-->3): 3--> cost: 0实例：垃圾回收公司成本问题 某城市有一家垃圾回收公司，负责该城市高新区的所有小区垃圾回收，目前 该公司有多辆垃圾营运专用车，每辆车均可收集多种垃圾。高新区内假定共有 N 个小区（小区编号从 0 开始到 N-1），共有 M 条垃圾车允许通行的路线，每条线 路均有相应的平均路程 S 和平均耗时 T。现要求根据给定的输入信息，编写程序 计算距离最短的路线，如果距离最短的路径存在多条，则要求输出时间最少的路 线。 代码： import sys sys.setrecursionlimit(100000000) # 弗洛伊德算法 def floyd(): n = len(graph) for k in range(n): for i in range(n): for j in range(n): if graph[i][k] + graph[k][j] < graph[i][j]: graph[i][j] = graph[i][k] + graph[k][j] T[i][j] = T[i][k] + T[k][j] parents[i][j] = parents[k][j] # 更新父结点 if graph[i][k] + graph[k][j] == graph[i][j]: if T[i][k] + T[k][j] < T[i][j]: graph[i][j] = graph[i][k] + graph[k][j] T[i][j] = T[i][k] + T[k][j] parents[i][j] = parents[k][j] # 更新父结点 # 打印路径 def print_path(i, j): if i != j: print_path(i, parents[i][j]) print(j, end='-->') n = int(input("n = ")) #n个点 m = int(input("m = ")) #m条边 start = int(input("start = ")) #起始点 end = int(input("end = ")) #目的点 inf = 9999999999 # 无穷大 datas = [[0]*4]*m for i in range(m): datas[i] = input().split(" ") #print(datas) # 构图 graph = [[(lambda x: 0 if x[0] == x[1] else inf)([i, j]) for j in range(n)] for i in range(n)] T = [[(lambda x: 0 if x[0] == x[1] else inf)([i, j]) for j in range(n)] for i in range(n)] # 耗时 parents = [[i] * n for i in range(n)] # 关键地方，i-->j 的父结点初始化都为i for u, v, s,t in datas: graph[u][v] = s T[u][v] = t floyd() S = graph[start][end] print_path(start,end) print(S, T[start][end]) # 最终的graph # graph[i][j]表示i-->j的最短路径 # 0 2 5 4 # 9 0 3 4 # 6 8 0 1 # 5 7 10 0 #
floyd算法(多源最短路径) python实现（主！） |
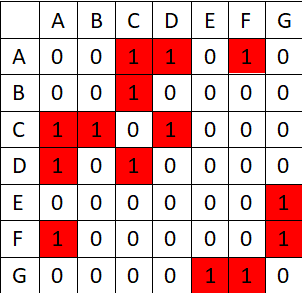data = [[0, 0, 1, 1, 0, 1, 0], [0, 0, 1, 0, 0, 0, 0], [1, 1, 0, 1, 0, 0x’x’x’x, 0], [1, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 1], [1, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 1, 1, 0]]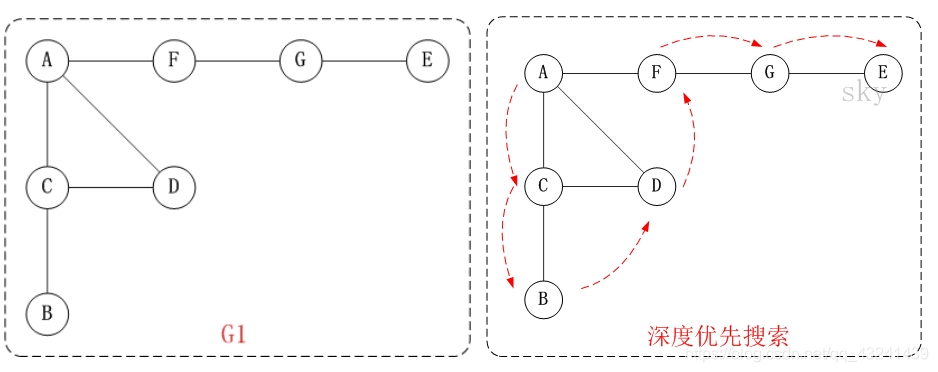
参考博客 ： 最短路径问题—Floyd算法详解 Floyd 算法最短路径问题精品（超详解） 最短路径—Dijkstra算法和Floyd算法（理解） 最优路径算法合集（附python源码）（原创）【本文地址】
今日新闻 |
推荐新闻 |