|
目录
一、结构方程模型的概念
二、结构方程模型的相关概念
三、结构方程模型的结构
四、结构方程的分析步骤
五、结构方程模型的应用
六、Amos结构方程分析实例
一、结构方程模型的概念
结构方程模型(Structural Equation Model,简称SEM)是基于变量的协方差矩阵来分析变量之间关系的一种统计方法,因此也称为协方差结构分析。结构方程模型属于多变量统计分析,整合了因素分析与路径分析两种统计方法,同时可检验模型中的显变量(测量题目)、潜变量(测量题目表示的含义)和误差变量直接按的关系,从而活动自变量对因变量影响的直接效果、间接效果和总效果。结构方程模型基本上是一种验证性的分析方法,因此通常需要有理论或者经验法则的支持,根据理论才能构建假设的模型图。在构建模型图之后,检验模型的拟合度,观察模型是否可用,同时还需要检验各个路径是否达到显著,以确定自变量对因变量的影响是否显著。目前,结构方程模型的分析软件较多,如Lisrel、EQS、Amos、Mplus、 Smartpls等等,其中AMOS的使用率甚高,因此我们重点了解一下使用AMOS软件进行结构方程模型分析的过程。结构方程包含两部分:测量模型,结构模型。测量模型研究的是潜变量(因子)和显变量(测量指标)的关系,简单点说可以认为因子分析就是测量模型,最典型的测量模型就是验证性因子分析;结构模型是研究潜变量之间或者说因子之间关系,及模型中无法解释的变异量(只有因子而没有测量因子的指标)
二、结构方程模型的相关概念
在构建模型假设图,我们首先需要了解一些有关的基本概念
显变量显变量有多种称呼,如“观察变量”、“测量变量”、“显性变量”、“观测变量”等等。从这些称呼中可以看到,显变量的主要含义就是:变量是实际测量的内容,也就是我们问卷上面的题目。在Amos中,显变量使用长方形表示。潜变量潜变量也叫潜在变量,是无法直接测量,但是可以通过多个题目进行表示的变量。在Amos中,潜变量使用椭圆表示。在使用的过程中,我们可以通过这样的方式区分显变量和潜变量:在数据文件中有具体值的变量就是显变量,没有具体值但可通过多个题目表示的则是潜变量。误差变量误差变量是不具有实际测量的变量,但必不可少。在调查中,显变量不可能百分之百的解释潜变量,总会存在误差,这反映在结构方程模型中就是误差变量,每一个显变量都会有误差变量。在Amos中,误差变量使用圆形进行表示(与潜变量类似)。拟合度拟合度,也叫适合度、配合度,是结构方程模型中最重要的指标。拟合度指标是假设的理论模型与实际数据的一致性程度,模型拟合度越高,代表理论模型与实际数据的吻合程度越高。Amos使用卡方作为拟合度检验的结果,一般以卡方值P>0.05作为标准,然而卡方容易受到样本大小的影响,因此除了卡方统计量之外,还需要参考其他拟合度指标。下表是常用的拟合度指标的判断标准(这些指标在Amos的“Output”中均能找到)。

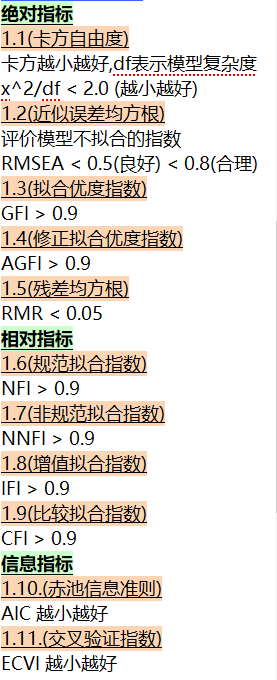
路径系数模型拟合度说明了理论模型与实际数据的一致性程度,而路径系数即路径系数检验则是说明变量之间的关系是否显著。路径系数包好标准路径系数和非标准路径系数,其含义与回归分析的路径系数相同。在路径系数检验的过程中,当系数的P值>0.05时,表明该路径的两个变量之间的影响不显著。此时,为了提高模型的拟合度,可将不显著的路径删除。在多变量的分析中中,经常会涉及到一个概念“效应值”。简单地说,效应值就是自变量对因变量的影响程度(这里的自变量和因变量都是潜变量),这种影响可以分为直接影响,还包含间接影响。在计算效应值的时候,我们需要知道各个路径的标准路径系数。
三、结构方程模型的结构
一个完整的结构方程模型需要包含两个方面:测量模型和结构模型。测量模型是指潜变量与显变量之间的额关系,结构模型是指潜变量之间的关系。下面以一个结构方程模型为例进行说明。【结构方程模型引例】研究者为了研究F1、F2和F3的关系,而设计了一份问卷,调查F1的题目(测量指标)有3个:X1、X2、X3;调查F2的题目有三道:Y1、Y2、Y3;调查F3的题目有三个:Z1、Z2、Z3。假设:假设1:F1能够直接影响F3;假设2:F2能够影响F3;假设3:F1可以通过F2影响F3。根据上述理论构想,可以构建如下的结构方程模型:

在上图中,F1、F2、F3为潜变量,X1~X3、Y1~Y3、Z1~Z3为显变量,e1~e9为误差变量。由e1~e3、X1~X3和F1构成的模型则是测量模型,由F1、F2、F3构成的则是结构模型。在进行假设检验之前,我们首先要通过Amos的“OutPut”了解模型的拟合度是否符合要求,当拟合度符合要求时,则可进行下一步的路径检验,如果模型的拟合度不符合要求,则需要对模型进行修正。在模型的拟合度符合要求之后,我们可以对F1、F2、F3之间的各条路径系数进行检验,如果系数具有显著意义,则认为该路径对应的假设处理。假如上述模型的拟合度不符合要求,并且F1→F3的路径不显著,那么可以采用删除F1→F3路径的方法对模型进行修正。对修正后的模型进行分析,发现模型的拟合度较好,并且保留的路径系数均显著,此时我们就可以得到结果,并对假设进行验证。根据上述分析,我们组中得到的结果为:F1对F3的直接影响不显著,F2对F3的影响显著,F2在F1和F3之间具有完全中介作用。也就是说,假设1不成立,假设2和假设3成立,并且F2在F1和F3之间具有完全中介效应。【附加内容】中介变量:X影响Y时,会通过中间项去影响,中间项即称为中介变量;自变量会影响到中介变量,同时中介变量还会影响到因变量。中介效应:如果中介变量存在,则称为有中介效应。部分中介效应:X影响Y时,一部分是直接影响,一部分是通过中介变量M去影响,此种情况则称为部分中介效应。完全中介效应:X影响Y时,如果全部是通过中介变量M去影响,即X要想影响Y,一定首先通过M才能影响到Y,此种情况则称为完全中介效应。如果上述模型的拟合度较好,并且各条路径系数均显著,那么就不需要对模型进行修正后,可以直接得到结果:F1对F3具有显著影响,F2对F3具有显著影响,F2在F1和F3之间具有部分中介作用。也就是:假设1、2、3均成立。此时,我们还需要使用标准路径系数计算自变量对因变量的效应值,假设F1→F2的标准路径系数为a,F2→的标准路径系数为b,F1→F3的标准路径系数为c,那么各个效应值的计算如下:

四、结构方程的分析步骤
1、需要对研究的内容有一个完整并且清晰的观念性架构;2、收集数据,并建立有效的原始数据文件(不能有缺失值)3、根据理论构想构建模型,也就是构建类似上图的模型结构;4、模型拟合度检验,如果模型拟合度良好,则可进行后续分析分析,如果模型拟合度不好,则需要对模型进行修正,直到拟合度符合表1的要求;5、路径系数检验,并计算各个潜变量之间的效应值。6、根据结构方程模型模型分析的结果得出结论,也就是验证假设。
五、结构方程模型的应用
结构方程模型最主要的应用就是分析多变量(≥3个)之间的关系,进行变量的中介效应检验。除此之外,还可以用来进行多群组的关系分析(可用来进行调节效应分析)。另外,研究者也常用测量模型进行问卷的效度分析(主要是验证性因素分析)。
六、Amos结构方程分析实例
此处等利用Amos解决实际研究问题时会再进行更新!
| 


