科幻小说《三体》里一种很魔幻的攻击方法——降维打击，以其神奇的作用方式和巨大的威力刷新了我们的三观。而在矩阵乘法计算中，这种降维打击时刻存在着。本节讲解一下矩阵乘法中造成的升维和降维。

还用游戏的例子，有4个角色，每个人都有不同的能力，将其用矩阵表示出来

现在我们要评估他们的两种能力：领兵打仗的能力和协同将领的能力

只要将两个矩阵相乘，就能根据 方法 X 对象 的法则评估出他们这两种能力值

我们生活中常见到的物体比如苹果，它是一个三维的物体，而当它被灯光照亮投影到地面上，它就形成了一个二维的影子。虽然通过影子我们也能看出来它大概的样子猜出它是一个苹果，但是它具体的颜色、红晕、斑纹的信息都消失了。

也可以用上一节中讲的空间变换来解释，将四维的对象在二维空间中展开了，得到的是二维空间中一个新的表现形式。

同样是这几个角色

我们多考察几种能力

得到的评估结果是

也可以用上一节中讲的空间变换来解释，将四维的对象在五维空间中展开了，并且通过添加其他信息扩展到了五维，得到的是五维空间中一个新的表现形式。

来看一个简单的矩阵乘法：

本来矩阵A可以张成一个二维空间， 但是经过左乘矩阵B之后，矩阵C却只能张成一个一维空间，也就是空间坍塌了！

原因是什么呢？是因为

它用来组成空间的两个基重叠了！导致二维空间坍塌成了一维空间。

   我们来看一下上面的A、B两个矩阵，它们的秩有什么问题

因为A中的两个向量它们线性无关， 它们的秩R(A)=2； B中的两个向量线性相关，它们的秩R(B)=1。

矩阵的秩，就是矩阵的列向量（或行向量）所能张成的空间的最大维度

（1） 若N个N维列向量线性无关，则它们可以张成N维空间，它们的秩就是满秩。

      举个例子： 组成矩阵D的 a、b、c 三个列向量线性无关，可以张成一个三维的空间。 

（2）若向量之间线性相关(则其中的一些向量可以用另一些向量表示出来，基有重叠），它们就无法张成一个满秩的空间。

举个例子： 组成矩阵F的3个列向量a1、a2、a3线性相关，虽然有3个向量，但是秩r(A)=2，只能张成二维空间。 

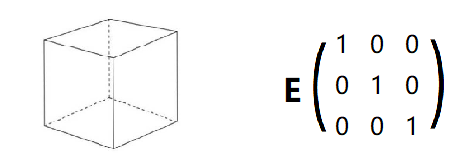
更进一步地，如果这些向量之间两两正交，则这些向量可以组成这个空间的一组基；如果再对这些基进行标准化，则这些基称为标准正交基。 

行列式的本质意义是什么呢？

从空间的伸缩性应该更容易理解一点。

单位矩E的行列式等于1， 它的行列式的几何意义可以看做是一个边长为1的超正方体的体积。 

对单位矩阵E的各个向量进行伸缩、平移、旋转之后，组成了一个超平行多面体，

行列式的几何意义就是行列式中的各列向量（或行向量）所构成的超平行多面体的有向体积（小于3维时为有向面积 ）。

从伸缩的角度来看，行列式可以看成是对单位矩阵的行列式各向量的伸缩，因此行列式的几何意义也可以看作

对单位矩阵的行列式体积的伸缩率。

那么，为什么不是满秩的矩阵它的行列式为0呢？

因为行列式就是体积的伸缩率，它遭到了降维打击，有的维度被踩扁了，在该方向上伸缩率变成了0，对所有的伸缩率进行叉乘的时候，不管有多少个伸缩率，|a|·|b|·|c|· |d|·0· cosα·cosβ·cosγ = 0 一定成立。 

你都把它踩扁了还指望它有能有体积吗？