常见概率分布及图像 |
您所在的位置:网站首页 › 二项分布的概率密度和分布函数的关系 › 常见概率分布及图像 |
常见概率分布及图像
|
概率分布
文章目录
概率分布@[toc]1 离散概率分布1.1 伯努利分布1.2 二项分布1.3 泊松分布
2 连续概率分布2.1 均匀分布2.2 指数分布2.3 正态分布2.4 卡方分布2.5 Student分布3.5 F分布
1 离散概率分布
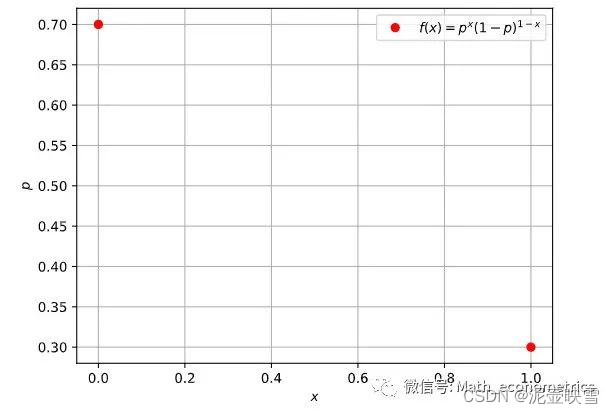
1.1 伯努利分布
随机变量 X X X仅取两个值, X = 0 , 1 X=0,1 X=0,1,概率质量函数(PMF)为
P
{
X
=
1
}
=
p
;
P
{
X
=
0
}
=
1
−
p
,
p
∈
[
0
,
1
]
P\{X=1\}=p; P\{X=0\}=1-p,p\in[0,1]
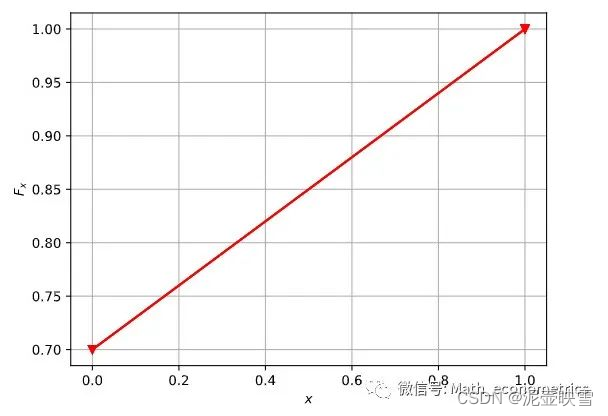
P{X=1}=p;P{X=0}=1−p,p∈[0,1] 伯努利累积概率分布(CMF) F ( X ≤ k ) F(X \le k) F(X≤k):
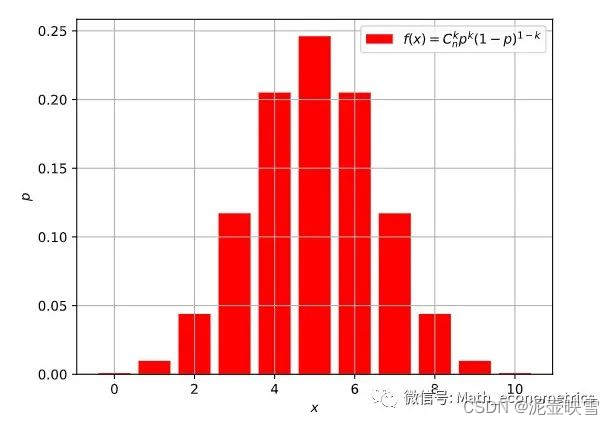
随机变量服从参数 n , p n,p n,p的二项分布,记作 X ∼ B ( n , p ) X\sim B(n,p) X∼B(n,p),PMF函数为 P { X = k } = ( k n ) p k ( 1 − p ) n − k , k = 0 , 1 , ⋯ n P\{X=k\}=\left(\begin{array}{c} k \\ n \end{array}\right) p^k(1-p)^{n-k} ,k=0,1, \cdots n P{X=k}=(kn)pk(1−p)n−k,k=0,1,⋯n 其中 ( n k ) = n ! k ! ( n − k ) ! \left(\begin{array}{l} n \\ k \end{array}\right)=\frac{n !}{k !(n-k) !} (nk)=k!(n−k)!n!是二项式系数。
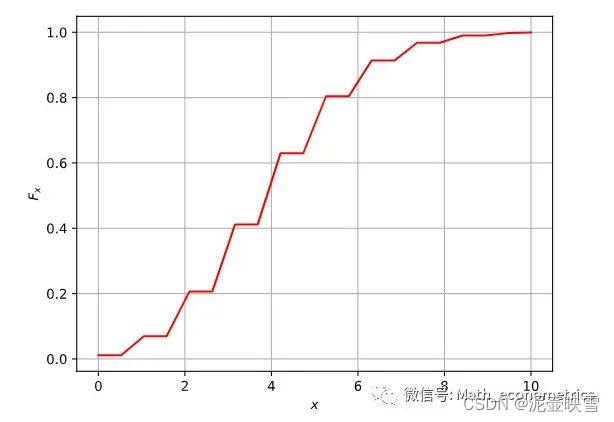
二项分布CMF:
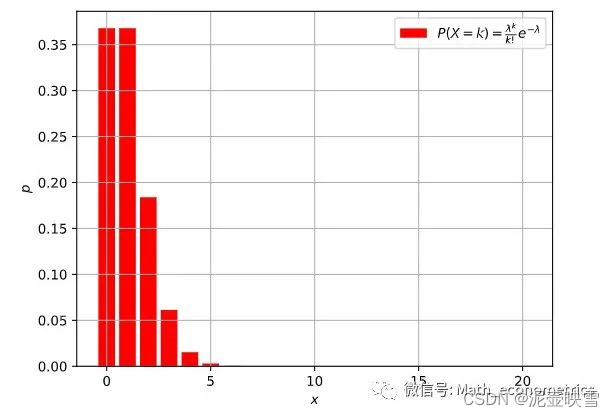
随机变量
X
X
X服从参数
λ
\lambda
λ,PMF为
P
(
X
=
k
)
=
λ
k
k
!
e
−
λ
,
k
=
0
,
1
,
⋯
P(X=k)=\frac{\lambda^k}{k !} e^{-\lambda}, k=0,1, \cdots
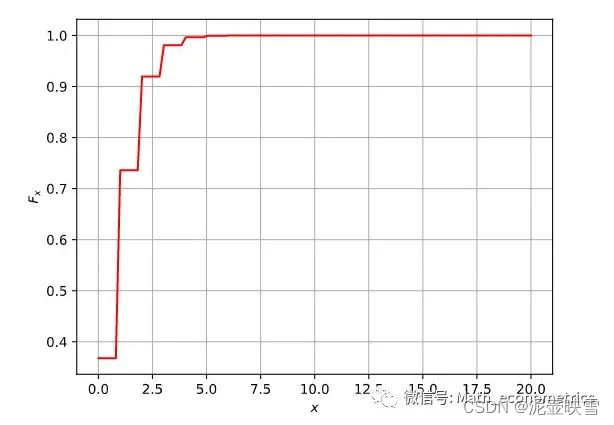
P(X=k)=k!λke−λ,k=0,1,⋯ 对应的CMF为
连续型随机变量
X
X
X服从均匀分布记作
X
∼
U
(
a
,
b
)
X\sim U(a,b)
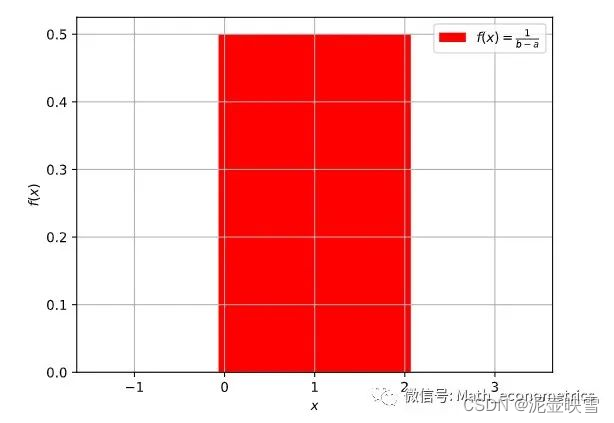
X∼U(a,b),概率密度函数(PDF)为
f
(
x
)
=
{
1
/
(
b
−
a
)
x
∈
[
a
,
b
]
0
e
l
s
e
f(x) = \left\{\begin{array}{l} 1/(b-a)& x\in[a,b] \\ 0&else \end{array}\right.
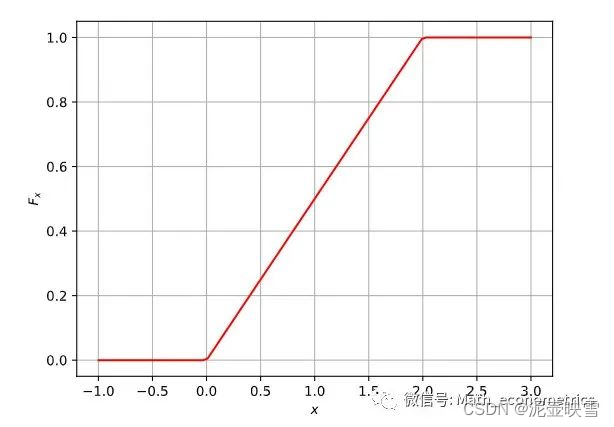
f(x)={1/(b−a)0x∈[a,b]else 均匀分布的累积概率分布为
F
(
x
)
=
{
0
,
x
≤
a
x
−
a
b
−
a
,
a
≤
x
≤
b
1
,
x
>
b
F(x)=\left\{\begin{array}{l} 0, x\le a \\ \dfrac{x-a}{b-a}, a\leq x \leq b \\ 1, x>b \end{array}\right.
F(x)=⎩
⎨
⎧0,x≤ab−ax−a,a≤x≤b1,x>b 连续型随机变量
X
X
X服从均匀分布记作
X
∼
E
(
λ
)
X\sim E(\lambda)
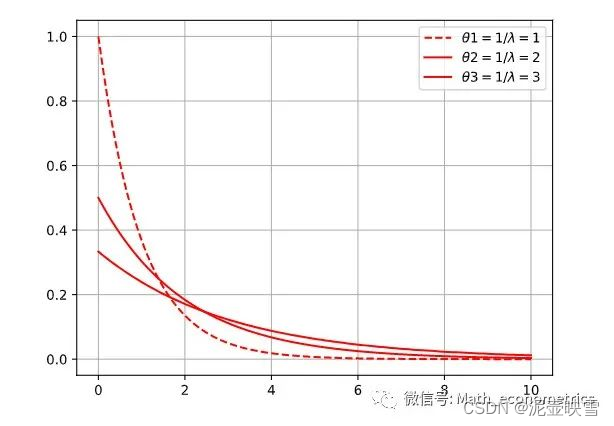
X∼E(λ),概率密度函数(PDF)为
f
(
x
)
=
{
λ
e
−
λ
x
x
>
0
0
x
⩽
0
f(x)=\left\{\begin{array}{l} \lambda e^{-\lambda x} &x>0 \\ 0&x \leqslant 0 \end{array}\right.
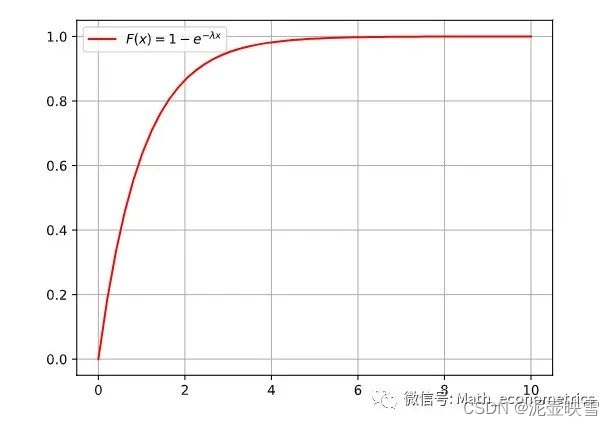
f(x)={λe−λx0x>0x⩽0 指数分布的累积概率分布为
P
{
X
≤
x
}
=
F
(
x
)
=
1
−
e
−
λ
x
,
x
>
0
P\{X \leq x\}=F(x)=1-e^{-\lambda x}, x>0
P{X≤x}=F(x)=1−e−λx,x>0 连续型随机变量
X
X
X服从正态分布记作
X
∼
N
(
μ
,
σ
2
)
X\sim N(\mu,\sigma^2)
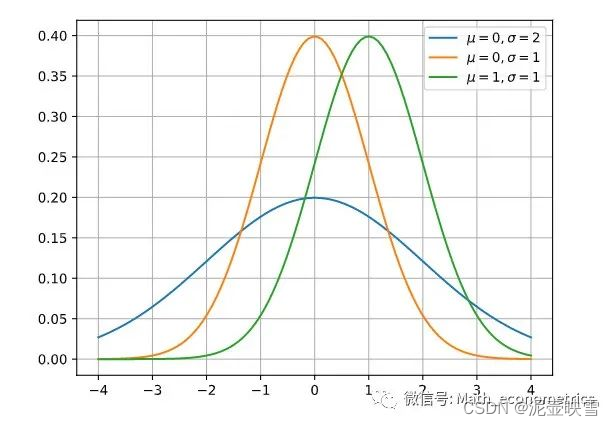
X∼N(μ,σ2),概率密度函数(PDF)为
f
(
x
)
=
1
2
π
σ
exp
(
−
(
x
−
μ
)
2
2
σ
2
)
f(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^2}{2 \sigma^2}\right)
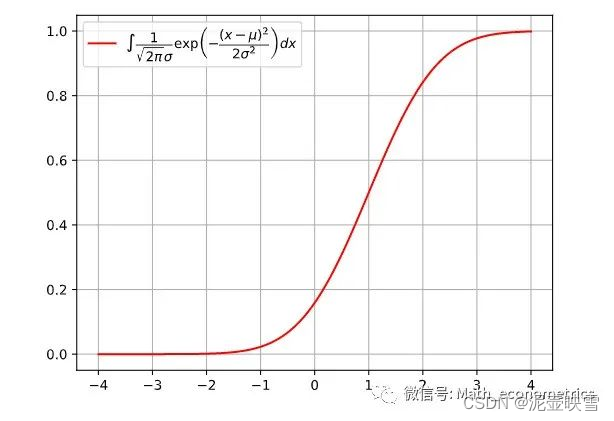
f(x)=2π
σ1exp(−2σ2(x−μ)2) 正态分布累积概率分布不存在初等函数,定义 F ( X ≤ k ) F(X\le k) F(X≤k)的概率为
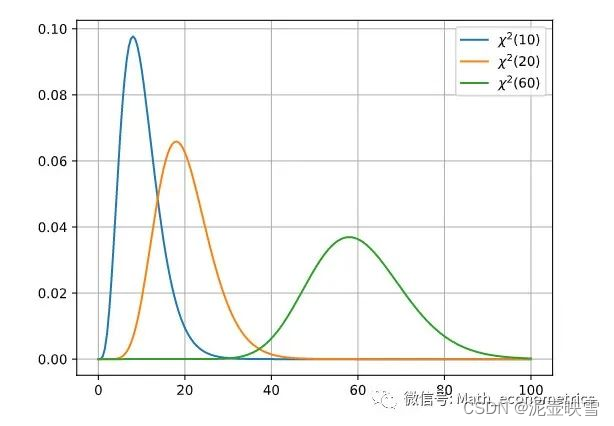
N N N个相互独立随机变量服从标准正态分布,则 N N N个随机变量的平方和服从 χ 2 \chi^2 χ2分布,记作 X ∼ χ 2 ( n ) X\sim\chi^2(n) X∼χ2(n), n n n为自由度。概率密度函数为 f k ( x ) = ( 1 / 2 ) k / 2 Γ ( k / 2 ) x k / 2 − 1 e − x / 2 , x > 0 f_k(x)=\frac{(1 / 2)^{k / 2}}{\Gamma(k / 2)} x^{k / 2-1} e^{-x / 2},x>0 fk(x)=Γ(k/2)(1/2)k/2xk/2−1e−x/2,x>0 Γ \Gamma Γ表示gamma函数。 k k k为自由度。
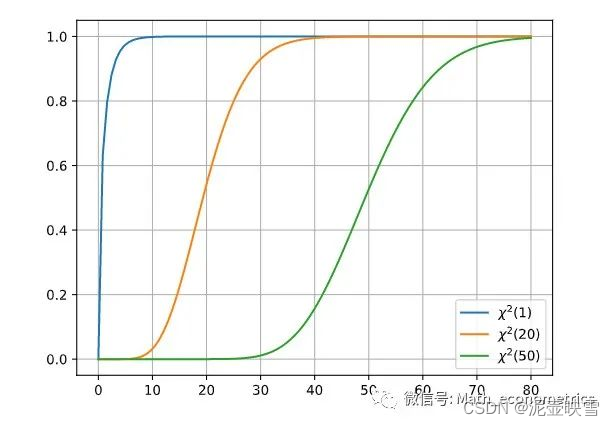
卡方分布累积概率分布为 F k ( x ) = γ ( k / 2 , x / 2 ) Γ ( k / 2 ) F_k(x)=\frac{\gamma(k / 2, x / 2)}{\Gamma(k / 2)} Fk(x)=Γ(k/2)γ(k/2,x/2) 其中 γ ( a , b ) \gamma(a,b) γ(a,b)表示不完全gamma函数。
随机变量
X
X
X服从标准正态分布,
Y
Y
Y服从
χ
2
(
n
)
\chi^2(n)
χ2(n),则随机变量
Z
=
X
Y
/
n
Z = \dfrac{X}{\sqrt{Y/n}}
Z=Y/n
X服从
t
t
t分布,概率密度函数为
f
Z
(
x
)
=
Γ
(
n
+
1
2
)
n
π
Γ
(
n
2
)
(
1
+
x
2
n
)
−
n
+
1
2
f_Z(x)=\frac{\operatorname{\Gamma}\left(\frac{n+1}{2}\right)}{\sqrt{n \pi} \operatorname{\Gamma}\left(\frac{n}{2}\right)}\left(1+\frac{x^2}{n}\right)^{-\frac{n+1}{2}}
fZ(x)=nπ
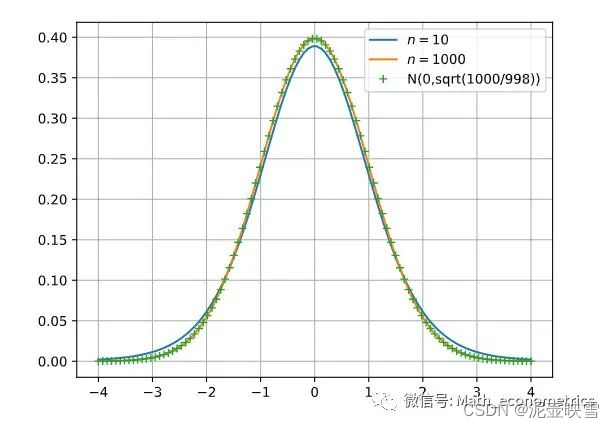
Γ(2n)Γ(2n+1)(1+nx2)−2n+1 当 n → ∞ n\to\infty n→∞,T分布与正态分布基本一致。 3.5 F分布随机变量
X
,
Y
X,Y
X,Y分别服从
χ
2
(
n
1
)
\chi^2(n_1)
χ2(n1)和
χ
2
(
n
2
)
\chi^2(n_2)
χ2(n2),则随机变量
Z
=
χ
2
(
n
1
)
/
n
1
χ
2
(
n
2
)
/
n
2
Z = \dfrac{\chi^2(n_1)/n_1}{\chi^2(n_2)/n_2}
Z=χ2(n2)/n2χ2(n1)/n1服从自由度为
(
n
1
,
n
2
)
(n_1,n_2)
(n1,n2)的
F
F
F分布,其pdf为
f
(
z
)
=
Γ
(
n
1
+
n
2
2
)
(
n
1
n
2
)
n
1
2
z
n
1
2
−
1
Γ
(
n
1
2
)
Γ
(
n
2
2
)
[
1
+
n
1
z
n
2
]
n
1
+
n
2
2
z
>
0
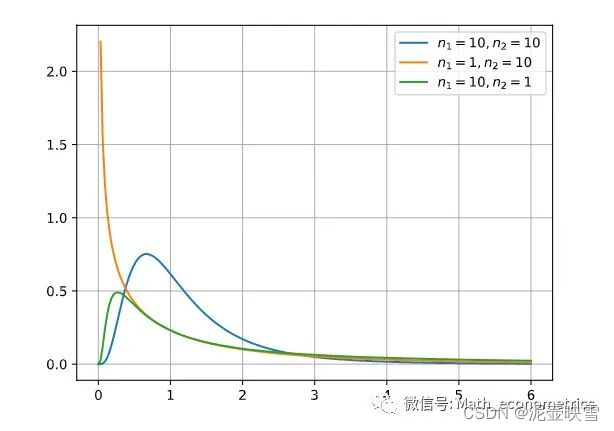
f(z)=\frac{\Gamma\left(\frac{n_1+n_2}{2}\right)\left(\frac{n_1}{n_2}\right)^{\frac{n_1}{2}} z^{\frac{n_1}{2}-1}}{\Gamma\left(\frac{n_1}{2}\right) \Gamma\left(\frac{n_2}{2}\right)\left[1+\frac{n_1 z}{n_2}\right]^{\frac{n_1+n_2}{2}}} \quad z>0
f(z)=Γ(2n1)Γ(2n2)[1+n2n1z]2n1+n2Γ(2n1+n2)(n2n1)2n1z2n1−1z>0 |
【本文地址】
今日新闻 |
推荐新闻 |