当我们试图用自变量的不同值所提供的信息来解二阶或更高阶的常微分方程时，我们必须使用与前面描述的不同的数值方法。 前面提到的初值问题经常涉及到“时间”作为自变量，解决技术要求我们按步骤“前进”，直到达到所需的解。在这种情况下，解的定义域不是有限的，因为原则上我们可以无限地沿着正方向或负方向前进。 边值问题涉及一个有限解的区间，在这个区间内去求解。这类问题的自变量通常是空间中测量距离的坐标。一个典型的二阶边值问题可能下面的形式。 解的定义域(假设为B >a)是由x在A≤x≤B的范围内的值给出的，我们需要的是找到对应于x在这个范围内的y的值。 本篇将考虑的数值解法分为三类 (a)用有限差分等效代替原来的微分方程的技术。 (b)“打靶法”，试图用一个等价初值问题代替边值问题。 ©“加权残差”法，即猜测一个满足边界条件的试解，并调整解内的某些参数以使误差最小化。

在这种方法中，微分方程中的导数项被有限差分近似代替。正如微分方程是线性的，将会显示的那样。这个过程会导致一个线性联立方程，可以使用前面描述的方法求解。 首先，需要定义一些有限差分近似来处理经常遇到的导数。考虑下图的解曲线，其中x轴被细分为规则的网格点，距离为h。 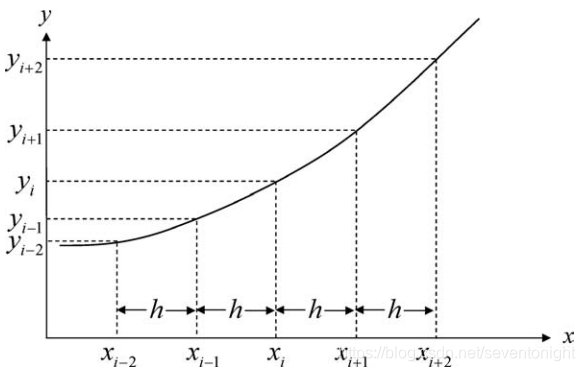可以用下面任意一种方法来表示y对x的一阶导数 这些有限差分公式通过计算函数在xi附近的连接点的直线的斜率来逼近一阶导数。正向和反向公式有偏差，因为它们只包括xi的右侧或左侧的点。中心差分形式将xi左右的点考虑在内。 高阶导数也可以用这种方法近似。例如，在xi处的二阶导数可以通过取一阶导数的逆向差来估计，如下所示 如果我们把一阶导数的前向差分公式代入，得到 类似上面可以得到yi’‘的中心差分公式 类似地，三阶导数的中心差分公式可以由 对x的四阶导数 这些高阶导数的正向和逆向差分也很容易得到，并且通过在差分公式中包含更多的点，可以获得更高的精度。 逆向差分公式是正向差分公式的简单镜像，除了奇数导数(即，y’，y " '等)，其中符号必须相反。 一阶导数在x0处的四点正向差分公式为 逆向差分公式为 “两点边值问题的解决方案包括把x的范围分裂到n个相等的部分,每个宽度h。n = 4,如果给定的边界条件,x = A和x = B,令ξ= x0 + ih, i = 1, 2,……，其中x0 = A, xn = B。 在每个点i = 1,2，…n−1处，微分方程以有限差分形式表示。如果微分方程是线性的，这将导致n−1个联立线性方程，在未知值yi, i = 1,2，…，n−1，其中yi表示在xi处的解。细分得越多，解的细节和精度就越高，但必须解决的联立方程也就越多。

给定y’’ = 3x + 4y，边界条件y(0) = 0, y(1) = 1，利用h = 0.2有限差分求解0≤x≤1范围内的方程。 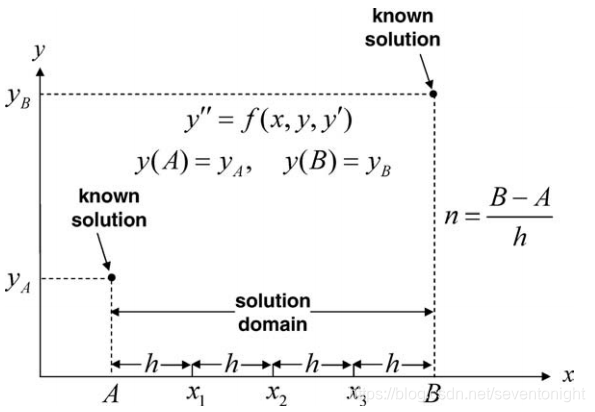首先将微分方程写成有限差分形式。选择二阶导数公式。通常使用最低阶中心差分形式，除非有特殊的情况去使用较不准确的正向或逆向差分形式，因此 微分方程可以写成 求解域被分割成5条相等的条带，每条宽度h = 0.2。 然后将有限差分方程写在每一个需要解的网格点上。需要时引入已知的边界条件，得到下表所示的四个方程。 这些(非对称)方程可以用线性方程求解中的任何合适的程序求解。第二个表将数值解与精确解进行了比较 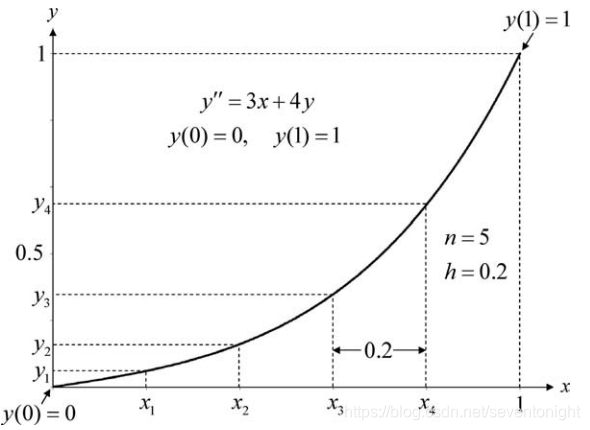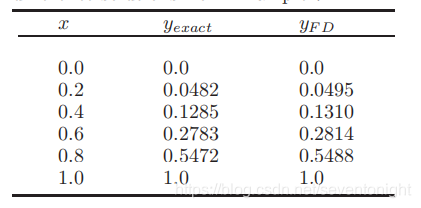显然，有限差分解的精度可以通过在0≤x≤1范围内进行更多的细分来进一步提高，但代价是求解更多的方程。 上个例子显示了一个问题，那就是如果使用了y "的高阶有限差分表示。例如，如果对y’‘使用五点中心差分公式，那么为了表示y1’‘和y4’’，就需要y在解域之外的值。为了解这个系统，还需要更多的信息，因为未知数要比方程多。 在解域之外引入点(至少是暂时引入点)的要求经常会碰到，并且可以通过采取合并适当的边界条件来解决，如下一个示例所示。 考虑一个边值问题 在这种情况下,y (B)是未知的,所以微分方程的有限差分需要写在x = B,即使使用最简单的中心差分公式y”，相应的“解决方案”在x5,将如下图所示。在这种情况下，我们有5个未知数，但只有4个方程。 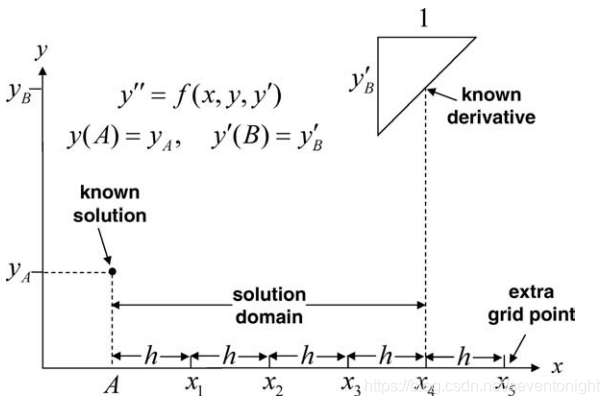第五个方程来自导数边界条件，它也可以写成有限差分形式，即使用中心差分

给定x2y’’ + 2xy’−2y = x2，边界条件y(1) = 1, y’(1.5) =−1。用h = 0.1有限差分求解1≤x≤1.5范围内的方程。 微分方程以有限差分形式，对两个导数项使用中心差分写成如下 并应用于5个需要解的x值，如下图所示。 得到的方程如下表所示。从下图可以看出，第五个方程在解域外引入了第六个未知数y6 = y(1.6)。中心差分形式的导数边界条件