5.4 导数与函数的极值、最值 |
您所在的位置:网站首页 › 二次函数求导求最值怎么求 › 5.4 导数与函数的极值、最值 |
5.4 导数与函数的极值、最值
|
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学下学期同步知识点剖析精品讲义! \(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\) 选择性必修第二册同步拔高,难度4颗星! 模块导图 知识剖析
极值的概念
知识剖析
极值的概念

若在点\(x=a\)附近的左侧\(f^{\prime} (x)0\), 则\(a\)称为函数\(y=f(x)\)的极小值点,\(f(a)\)称为函数\(y=f(x)\)的极小值; 若在点\(x=b\)附近的左侧\(f^{\prime} (x)>0\),右侧\(f^{\prime} (x)0$时,$f^{\prime}(x)>0$;
故根据极值的定义,$0$不是函数$f(x)=x^3$的极值点,这个从函数图象也很容易知道.
又如函数$g(x)=|x|$,
总结 ① 若\(f(x)\)可导,且\(x_0\) 是\(y=f(x)\)的极值,则\(x_0\)是\(f^{\prime}(x)=0\)的解; ② 若\(x_0\)是\(f^{\prime}(x)=0\)的解,\(x_0\) 不一定是\(y=f(x)\)的极值点. ③ 定义很重要. 求函数的极值的方法解方程\(f^{\prime}(x)=0\),当 \(f^{\prime}(x_0)=0\)时: (1) 如果在\(x_0\)附近的左侧\(f^{\prime} (x)>0\),右侧\(f^{\prime}(x)0 \\ a>0 \end{array}\right.\),解得\(00\), 故选:\(D\). 【点拨】 ① \(x_0\)是\(y=lnx+1+2x\)的零点,可用零点判定定理判断\(x_0\)的大致范围,这属于“隐零点问题”; ②\(x_0\)是可导函数\(f(x)\)的极值点,则满足\(f^{\prime}(x_0 )=0⇒lnx_0=-1-2x_0\),可化简\(g(x_0 )=f(x_0 )+2x_0\)再求它最值. 【典题2】讨论\(f(x) =x^2+(m-2)x-mlnx\)的极值点的个数. 【解析】函数的定义域为\((0 ,+∞)\), \(f^{\prime}(x)=2 x+m-2-\dfrac{m}{x}\)\(=\dfrac{2 x^{2}+(m-2) x-m}{x}\)\(=\dfrac{(2 x+m)(x-1)}{x}\), 令\(f^{\prime}(x)=0\),得\(x=-\dfrac{m}{2}\)或\(x=1\), ① 当\(-\dfrac{m}{2}>1\),即\(m0\), 在\((1 ,-\dfrac{m}{2})\)上,\(f'(x)0\), \(∴f(x)\)在\((-1 ,x_1)\)上单调递增; 当\(x_10\), \(∴f(x)\)在\((x_2 ,+∞)\)上单调递增. \(∴\)当\(f(x)\)有两个极值点时,\(a\)的取值范围为\((8 ,+∞)\). (2)由①可知,函数\(f(x)\)有唯一的极小值点为\(x_2\),且\(-\dfrac{3}{4}-1\) 恒成立,即\(A\)正确; 选项\(B\), 设\(g(x)=lnx-x+1(x>0)\), 令\(g^{\prime}(x)=\dfrac{1}{x}-1=0 \Rightarrow x=1\), \(∴g(x)\)在\((0 ,1)\)上递增,在\((1 ,+∞)\)上递减, \(∴g(x)≤g(1)=0\), 即\(lnx≤x-1\),即\(B\)错误; 选项\(C\), 设\(h(x)=e^x-x-1\),则\(h^{\prime} (x)=e^x-1\) 令\(h'(x)=0\),解得\(x=0\), 当\(x0\),\(h(x)\)单调递增. \(∴h(x)_{min}=h(0)=0\), 即\(h(x)≥0\)在\(R\)上恒成立, \(∴e^x≥x+1\)恒成立,即\(C\)正确; 选项\(D\), 设\(t(x)=\cos x-1+\dfrac{1}{2} x^{2}\),则\(t^{\prime}(x)=-\sin x+x\) 令\(m(x)=t^{\prime}(x)=-\sin x+x\), 则\(m^{\prime}(x)=-cosx+1≥0\)恒成立, 即\(m(x)\)在\(R\)上单调递增,又\(m(0)=0\), \(∴\)当\(x0\),\(t(x)\)单调递增. \(∴t(x)_{min}=t(0)=0\), 即\(t(x)≥0\)在\(R\)上恒成立, \(∴\cos x \geq 1-\dfrac{1}{2} x^{2}\)恒成立,即\(D\)正确. 故选:\(ACD\). 【点拨】 ① 通过构造函数证明不等式,选项\(D\)中运用了二次求导; ② 研究函数的最值,其实最终还是回归到函数单调性的分析,注意结合导函数的“穿线图”与原函数的“趋势图”进行分析函数最值; ③ 熟记\(e^x≥x+1\),\(lnx≤x-1\),以后你们会经常见到它们. 比如\(\ln x \leq x-1 \stackrel{\text { 令 } x=\frac{1}{x}}{\Longrightarrow} \ln x \geq 1-\dfrac{1}{x}\)\(\stackrel{\text { 令 } x=x+1}{\Longrightarrow} \ln (x+1) \geq \dfrac{x}{x+1}(x>-1)\),这就容易得知\(A\)正确. 【典题2】若函数\(f(x)=\dfrac{2}{3} x^{3}-a x^{2}(a0,2x-1>0,则导函数y=f'(x)的正负性等价于}}\) \({\color{Red}{ y=ax-1在[1 ,e]上的正负性,比较\dfrac{1}{a}与1、e的大小进行分类讨论)}}\) ①当\(00\),\(f(x)\)在\([1 ,e]\)上单调递增, 所以\(f(x)\)在\([1 ,e]\)上的最小值是\(f(1)=-2\); ②当\(1 |
【本文地址】
今日新闻 |
推荐新闻 |
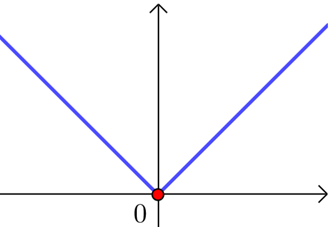 当$x0$;
所以$g(x)$在$x=0$处取到极值,但在导数不存在;故选$C$.
当$x0$;
所以$g(x)$在$x=0$处取到极值,但在导数不存在;故选$C$.