|
求整数N的开方,精度在0.001
二分法
若N大于1,则从[1, N]开始,low = 1, high = N, mid = low + (high - low) >> 1开始进行数值逼近
若N小于1,则从[N, 1]开始,low = 0, high = N, mid = low + (high - low) >> 1开始进行数值逼近
#include
#include
#include
#define ACCURACY 0.001
double newSqrt(double n)
{
double low, high, mid, tmp;
// 获取上下界
if (n > 1) {
low = 1;
high = n;
} else {
low = n;
high = 1;
}
// 二分法求开方
while (low n) {
high = mid;
} else {
low = mid;
}
}
return -1.000;
}
int main(void)
{
double n, res;
while (scanf("%lf", &n) != EOF) {
res = newSqrt(n);
printf("%lf\n", res);
}
return 0;
}
牛顿迭代法思路求解:
#include
using namespace std;
int main()
{
int N;
coutN
double x1 = 1;//初值
double x2 = x1/2.0+N/2.0/x1;
while( fabs(x2-x1)>0.001)
{
x1 = x2;
x2 = x1/2.0+N/2.0/x1;
}
cout return x; } while(sum_n unsigned long sum_n = 0; unsigned n = (x >> 1); unsigned top = x; unsigned bottom = 0; if (x sum_n = n * n; if (sum_n top = n; n -= ((top - bottom) >>1); if (n == top) return n-1; } else { return n; } } }
算法2 Newton 法
把这个问题转换为方程求根问题,即: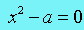 ,求x。 ,求x。
而方程求根的问题可以用Newton 法来解决。现在的问题有一点不同,即所求的根必须是整数。通过证明,我们可以发现,Newton迭代公式是适用于整数情况的,于是有:
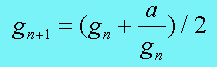 至于是怎么证明的,可以参考hacker’s delight。 至于是怎么证明的,可以参考hacker’s delight。
另外,初值的选择也是很重要的一环,这里我们选择大于等于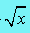 的最小的2的幂次数。 的最小的2的幂次数。
OK,下面给出程序:
 unsigned newton_method(unsigned
long x)
{
unsigned
long x1 = x -
1;
unsigned s =
1;
unsigned g0,g1;
/*
初值设定 通常将初始值设为1,但是只有1的开方才会是1,通过预处理找到更精确地初始值a[n]
*/
if (x1 >
65535) {s +=
8; x1 >>=
16;}
if (x1 >
255) {s +=
4; x1 >>=
8;}
if (x1 >
15) {s +=
2; x1 >>=
4;}
if (x1 >
3) {s +=
1; x1 >>=
2;}
/*
迭代
*/
g0 =
1 s)) >>
1;
while(g1 >
1;
}
return g0;
}
unsigned newton_method(unsigned
long x)
{
unsigned
long x1 = x -
1;
unsigned s =
1;
unsigned g0,g1;
/*
初值设定 通常将初始值设为1,但是只有1的开方才会是1,通过预处理找到更精确地初始值a[n]
*/
if (x1 >
65535) {s +=
8; x1 >>=
16;}
if (x1 >
255) {s +=
4; x1 >>=
8;}
if (x1 >
15) {s +=
2; x1 >>=
4;}
if (x1 >
3) {s +=
1; x1 >>=
2;}
/*
迭代
*/
g0 =
1 s)) >>
1;
while(g1 >
1;
}
return g0;
}
算法3 逐比特确认法
逐比特确认法认为一个32位整数求根,结果应该是一个16位整数。求这个16位整数,其实质是确认每位的比特是0还是1.我们把这个根分为两个相加的部分,一部分是已确认的值,另一部分是未确认的值。从高位到低位,每次迭代确认一位。初始时,已确认部分为0。则问题的初始形式为:
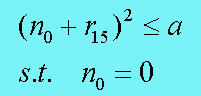 算法发明者为:James Ulery 论文:Computing Integer Square Roots 算法发明者为:James Ulery 论文:Computing Integer Square Roots
下面给出源代码:
 unsigned bitwise_verification(unsigned
long x)
{
unsigned
long temp =
0;
unsigned v_bit =
15;
unsigned n =
0;
unsigned b =
0x8000;
if (x 接下来介绍一种手动模拟求平方根算法。非常巧妙,非常神奇。可能自己智商有点问题哈,仔细琢磨了几个小时才彻底明白。先仔细介绍如何使用这种算法模拟求平方根,然后再简要说一说它的原理吧!
(a)首先将要开方根的数从小数点分别向右及向左每两个位一组分开,如98765.432内小数点前的65是一组,87是一组,9是一组,小数点后的43是一组,之后是单独的一个2,要补一个0而得20是一组。
(b)将最左一组的数减去最接近又不大于它的平方数,并将该平方数的开方(应该是个位数)记下。
(c) 将上一步所得之差乘以100,和下一组数加起来。
(d)将记下的数乘以20,然后将它加上某个个位数,再乘以这个个位数,令这个积不大于又最接近上一步所得之差,并将该个位数记下,且将上一步所得之差减去所得之积。
(e)记下的数依次隔两位记下。
(f)重复第3步,直到找到答案。
(g) 可以在数字的最右补上多组的00,以求得理想的精确度未止。
unsigned bitwise_verification(unsigned
long x)
{
unsigned
long temp =
0;
unsigned v_bit =
15;
unsigned n =
0;
unsigned b =
0x8000;
if (x 接下来介绍一种手动模拟求平方根算法。非常巧妙,非常神奇。可能自己智商有点问题哈,仔细琢磨了几个小时才彻底明白。先仔细介绍如何使用这种算法模拟求平方根,然后再简要说一说它的原理吧!
(a)首先将要开方根的数从小数点分别向右及向左每两个位一组分开,如98765.432内小数点前的65是一组,87是一组,9是一组,小数点后的43是一组,之后是单独的一个2,要补一个0而得20是一组。
(b)将最左一组的数减去最接近又不大于它的平方数,并将该平方数的开方(应该是个位数)记下。
(c) 将上一步所得之差乘以100,和下一组数加起来。
(d)将记下的数乘以20,然后将它加上某个个位数,再乘以这个个位数,令这个积不大于又最接近上一步所得之差,并将该个位数记下,且将上一步所得之差减去所得之积。
(e)记下的数依次隔两位记下。
(f)重复第3步,直到找到答案。
(g) 可以在数字的最右补上多组的00,以求得理想的精确度未止。
 原理网上说是(a+b)^2 = a^2 + b^2 + 2ab = a^2 + (2a+b)*b。并没有完全看明白,这里就不班门弄斧了,等以后搞清楚,再补上吧!
/* 大整数开方 ,模拟手工开方*/
# include
# include
# include
# include
# include
# define MAXN 1001
void bigN_sqrt(char *s);
int bigN_cmp(char *a, char *b, int lim);
void bigN_mul(char *a, int k, int lim);
void bigN_add(char *a, int k);
void bigNN_minus(char *a, char *b, int lim);
int Newtonsqrt(double x); //牛顿迭代可求求64位数的平方根
char str[MAXN];
int main()
{
freopen("hugeint.in", "r", stdin);
freopen("hugeint.out", "w", stdout);
while (~scanf("%s", str))
bigN_sqrt(str);
// printf("time cost %.3lfs.\n", (double)clock()/CLOCKS_PER_SEC);
return 0;
}
int bigN_cmp(char *a, char *b, int lim)
{
int i;
for (i = lim-1; i >= 0; --i)
if (a[i] < b[i]) return 1;
else if (a[i] > b[i]) return -1;
return 0;
}
void bigN_mul(char *a, int k, int lim)
{
int i, tmp, c;
for (c=i=0; i < lim; ++i) {
tmp = a[i]*k + c;
c = tmp / 10;
a[i] = tmp - 10*c;
}
}
void bigN_add(char *a, int k)
{
int i = 0;
while (k > 0) {
a[i++] += k%10;
k /= 10;
}
}
void bigNN_minus(char *a, char *b, int lim) // b = b - a;
{
int i, tmp, c;
for (c=i=0; i < lim; ++i) {
tmp = b[i] - a[i] + c;
c = (tmp0.1)
{
x1 = x2;
x2 = x1/2.0+x/2.0/x1;
}
return floor(x1);
}
void bigN_sqrt(char *s)
{
short int i, k, slen; // 根的一个十进制位
char res[MAXN]; // 试方余数
char cur[MAXN]; // 试方上限
char tmp[MAXN];
int lim;
memset(res, 0, sizeof(res));
memset(cur, 0, sizeof(cur));
lim = slen = strlen(s);
if (slen < 18) {
//非大整数,直接调用sqrt()计算平方根,结束 。sqrt()计算平方根并非完全正确,在测试的过程中
// sqrt(8456552264) = 91960 ,而实际上 8456552264的平方根是91959 ,因此采用Newton迭代法求解
// printf("%.0lf\n", sqrt(atof(s)));
// printf("%.0lf\n", sqrt(8456552264));
double value=atof(s);
printf("%d",Newtonsqrt(value));
return ;
}
if (slen & 0x1) {
k = -1;
cur[0] = s[0] - 48;
} else {
k = 0;
cur[1] = s[0] - 48;
cur[0] = s[1] - 48;
}
while (1) {
i = 0;
while (1) {
++i;
memcpy(tmp, res, MAXN);
bigN_mul(tmp, i*20, lim);
bigN_add(tmp, i*i);
if (-1 == bigN_cmp(tmp, cur, lim)) break; // break until tmp > cur;
}
--i;
printf("%d", i);
memcpy(tmp, res, MAXN); //cur -= res*i*20+i*i;
bigN_mul(tmp, i*20, lim);
bigN_add(tmp, i*i);
bigNN_minus(tmp, cur, lim);
bigN_mul(res, 10, lim); // res = res*10+i;
bigN_add(res, i);
k += 2;
if (k >= slen) break;
else {
bigN_mul(cur, 100, lim);
bigN_add(cur, ((s[k]-48)*10+(s[k+1]-48)));
}
}
printf("\n");
}
原理网上说是(a+b)^2 = a^2 + b^2 + 2ab = a^2 + (2a+b)*b。并没有完全看明白,这里就不班门弄斧了,等以后搞清楚,再补上吧!
/* 大整数开方 ,模拟手工开方*/
# include
# include
# include
# include
# include
# define MAXN 1001
void bigN_sqrt(char *s);
int bigN_cmp(char *a, char *b, int lim);
void bigN_mul(char *a, int k, int lim);
void bigN_add(char *a, int k);
void bigNN_minus(char *a, char *b, int lim);
int Newtonsqrt(double x); //牛顿迭代可求求64位数的平方根
char str[MAXN];
int main()
{
freopen("hugeint.in", "r", stdin);
freopen("hugeint.out", "w", stdout);
while (~scanf("%s", str))
bigN_sqrt(str);
// printf("time cost %.3lfs.\n", (double)clock()/CLOCKS_PER_SEC);
return 0;
}
int bigN_cmp(char *a, char *b, int lim)
{
int i;
for (i = lim-1; i >= 0; --i)
if (a[i] < b[i]) return 1;
else if (a[i] > b[i]) return -1;
return 0;
}
void bigN_mul(char *a, int k, int lim)
{
int i, tmp, c;
for (c=i=0; i < lim; ++i) {
tmp = a[i]*k + c;
c = tmp / 10;
a[i] = tmp - 10*c;
}
}
void bigN_add(char *a, int k)
{
int i = 0;
while (k > 0) {
a[i++] += k%10;
k /= 10;
}
}
void bigNN_minus(char *a, char *b, int lim) // b = b - a;
{
int i, tmp, c;
for (c=i=0; i < lim; ++i) {
tmp = b[i] - a[i] + c;
c = (tmp0.1)
{
x1 = x2;
x2 = x1/2.0+x/2.0/x1;
}
return floor(x1);
}
void bigN_sqrt(char *s)
{
short int i, k, slen; // 根的一个十进制位
char res[MAXN]; // 试方余数
char cur[MAXN]; // 试方上限
char tmp[MAXN];
int lim;
memset(res, 0, sizeof(res));
memset(cur, 0, sizeof(cur));
lim = slen = strlen(s);
if (slen < 18) {
//非大整数,直接调用sqrt()计算平方根,结束 。sqrt()计算平方根并非完全正确,在测试的过程中
// sqrt(8456552264) = 91960 ,而实际上 8456552264的平方根是91959 ,因此采用Newton迭代法求解
// printf("%.0lf\n", sqrt(atof(s)));
// printf("%.0lf\n", sqrt(8456552264));
double value=atof(s);
printf("%d",Newtonsqrt(value));
return ;
}
if (slen & 0x1) {
k = -1;
cur[0] = s[0] - 48;
} else {
k = 0;
cur[1] = s[0] - 48;
cur[0] = s[1] - 48;
}
while (1) {
i = 0;
while (1) {
++i;
memcpy(tmp, res, MAXN);
bigN_mul(tmp, i*20, lim);
bigN_add(tmp, i*i);
if (-1 == bigN_cmp(tmp, cur, lim)) break; // break until tmp > cur;
}
--i;
printf("%d", i);
memcpy(tmp, res, MAXN); //cur -= res*i*20+i*i;
bigN_mul(tmp, i*20, lim);
bigN_add(tmp, i*i);
bigNN_minus(tmp, cur, lim);
bigN_mul(res, 10, lim); // res = res*10+i;
bigN_add(res, i);
k += 2;
if (k >= slen) break;
else {
bigN_mul(cur, 100, lim);
bigN_add(cur, ((s[k]-48)*10+(s[k+1]-48)));
}
}
printf("\n");
}
|
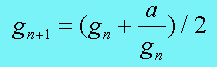 至于是怎么证明的,可以参考hacker’s delight。
至于是怎么证明的,可以参考hacker’s delight。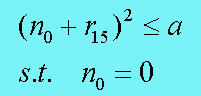 算法发明者为:James Ulery 论文:Computing Integer Square Roots
算法发明者为:James Ulery 论文:Computing Integer Square Roots