小波变换的理解 |
您所在的位置:网站首页 › 专业检索的优缺点是什么意思 › 小波变换的理解 |
小波变换的理解
|
文章目录
前言一、傅里叶变换的劣势以及小波变换的优势二、连续小波变换(CWT)的理解2.1 什么是小波变换?2.2 为什么小波变换能确定信号频率和其对应的时间区间?2.3 连续小波变换最大的特点是什么?2.4 其它补充
三、离散小波变换(DWT)的理解3.1 离散小波变换(DWT)定义3.2 一维离散小波变换3.3 二维离散小波变换3.4 离散小波变换(DWT)的Mallet算法(离散化实现)3.5 离散小波变换(DWT)的应用
四、总结
前言
小波变换:用于提取信号的局部特征(时域+频域信息) 小波变换是在傅里叶变换的基础上,发展而来,因此,在学习小波变换之前,需要对傅里叶变换有一定的了解。(傅里叶变换的内容在之前的实例中有介绍,这里不作赘述,详见对音频信号作短时傅里叶变换(STFT)/小波变换处理(python + matlab ;傅里叶变换(FT)) 一、傅里叶变换的劣势以及小波变换的优势傅里叶变换的基函数是三角函数,其作用域是信号的整个时间域,无法得到信号的局部特征(即只能获取一段信号总体上包含哪些频率的成分,但是对各成分出现的时刻并无所知);尽管采用“加窗”的思想,改进得到短时傅里叶变换,可以提取信号得局部特征,但是由于短时傅里叶变换窗口固定,宽度相等,其特征提取效果并不好,无法满足非稳态信号变化的特征需求,故而引入小波变换,使得“窗口宽度”不一致(小波变换的思想不是加窗,而是通过尺度a分别同时与中心频率和基函数支撑区间产生关系,在这里可以形象化的理解为加窗,后续会进一步解释),从而更好的实现局部特征提取。 通过前面的阐述,我们知道了小波变换的优势,它可以对非稳态信号做时频分析。接下来,我们进一步了解,什么是小波变换?为什么小波变换能确定信号的频率和其对应的时间区间? 2.1 什么是小波变换?小波变换: 将傅里叶变换中无限长的三角函数基换成了有限长的会衰减的小波基。
小波变换公式: 小波变换的两个变量: 从公式可以看出,不同于傅里叶变换,变量只有频率w,小波变换有两个变量:尺度a(scale)和平移量 ζ(translation)。尺度a控制小波函数的伸缩,平移量 ζ控制小波函数的平移。尺度a就对应于频率(反比),平移量ζ就对应于时间。
举个例子: 假设时域信号如下: 小波变换还有一些好处,比如,我们知道对于突变信号,傅里叶变换存在吉布斯效应,我们用无限长的三角函数怎么也拟合不好突变信号: 不确定性原理,或者叫做测不准原理,最早出自量子力学,意为在微观世界,离子的位置与动量不可同时被确定。但是这个原理并不局限于量子力学,有很多物理量都有这样的特征,比如能量和时间、角动量和角度。体现在信号领域就是时域和频域。不过更准确一点的表述应该是:一个信号不能再时空域和频域上同时过于集中;一个函数时域窄,它经过傅里叶变换的频域后就越宽。 问题二、关于正交化什么是正交化?为什么说小波能实现正交化是优势? 简单说,如果采用正交基,变换域系数会没有冗余信息,变换前后的信号能量相等,等于是用最少的数据表达最大的信息量,利用数值压缩等领域。 问题三、关于瞬时频率,图中时刻点对应一频率值,一个时刻点只有一个信号值,又怎么能得到他的频率呢?很好的问题。如文中所说,绝对意义的瞬时频率其实是不存在的,但看一个时刻点的一个信号值,当然得不到他的频率。我们只不过是很短的一段信号的频率作为该时刻表的频率,所以我们得到的只是时间分辨率有限的近似分析结果。这一想法在STFT上体现的很明显,小波用衰减的基函数去测定信号的瞬时频率,思想也类似 小结: 傅里叶变换: 知道一段时间内,信号各个频率分量分别多少; 小波变换: 知道一段时间内,信号的各个频率分量分别是多少,以及他们都是什么时候出现的。 2.2 为什么小波变换能确定信号频率和其对应的时间区间?这个问题可以一分为二的来看,即,1. 为什么CWT能辨认出信号的频率成分?2. 为什么CWT能确定频率对应的时间区间? morlet小波基函数分析:以一个morlet小波基函数为例进行说明,其表达式如下: 上述是对小波基函数的描述,现在回到小波变换,于是morlet小波变换的公式有: 举个例子: 一个频率为5的正弦函数 y=sin(2pi5t),和 f=sin(2pint),n=1,2,…,n,乘积后积分,问当频率为何值时,他们的乘积积分后结果最大。答案你肯定知道,当两个正弦函数频率相等的时候,而就是n=5的时候,他们的乘积积分后最大。有图为证: 接下来,把 f 换成小波基函数,换成morlet小波函数,去掉平移参数,并令初始中心频率 W0=10,令尺度参数 a=1,2,…10: 多分辨分析肯定是标准答案。所谓多分辨分析即是指小波在不同频率段会有不同的分辨率。 举个例子: 假设信号为: 举个例子: 假设有5个中心频率不同的小波基函数,如下: 对比两组基函数表达式,如下: 如果把基函数时域支撑区间叫做窗口长度,那么图四对应的就是窗口不变的傅里叶变换,即我们熟悉的另一种时频变换—加窗傅里叶变换(也就是短时傅里叶变换STFT),而图三对应的就是窗口可变的傅里叶变换,这就是我们要讲解的小波变换。 对于时间分辨率:我们知道,傅里叶变换是一个全局整体的积分,所以是没有时间分辨率的,如果,对信号进行分段的傅里叶变换,也就是加窗傅里叶变换,那么每一段时域信号便会对应一个频谱,这个时候,时间分辨率就出来了,如果加的窗口越短,定位的时间越准确,时间分辨率越高。 不同窗口长度下的STFT,如下图五、六所示: 而小波变换中,通过尺度a分别同时与中心频率和基函数支撑区间产生关系,使得时间,频率分辨率和频率产生关系。 小结: 尺度a是一个很重要的参数,因为它不仅仅能产生一系列中心频率不同的小波基函数(带通滤波器),还可以控制基函数在时域的支撑区间(带通滤波器的带宽),进而控制时间分辨率和频率分辨率。所以,表现出来的就是时间分辨率和频率有一定的关系。 尺度a越大,支撑区间的长度越长(形象化理解为STFT的窗口长度),频率分辨率越高,时间分辨率越低,反之亦然。
为什么在信号处理中只用傅里叶变换和小波变换? 信号处理怎么会 只有傅里叶变换和小波呢,只不过用的多些罢了(哈哈),这个要具体问题具体分析,如果是平稳周期信号,当然是傅里叶比较好,如果是非平稳非周期信号(常见的)当然是小波比较好,所谓的变换也不过是“搞基”,基就是描述信号特征的特征向量,而像傅里叶和小波这些比较固定的基,未必是对信号的一个最好的描述。 傅里叶变换、拉氏变换、Z变换干啥用的,三者之间的关系? 傅里叶分析包含傅里叶级数与傅里叶变换。傅里叶级数用于对周期信号转换,傅里叶变换用于非周期信号转换。 但对于不收敛的信号,傅里叶变换无能为力,只能借助拉普拉斯变换(添加了衰减函数),主要用于计算微分方程,而Z变换则可以算作是离散的拉普拉斯变换(主要计算差分方程)。 从复平面来说,傅里叶分析注意虚数部分,拉普拉斯变换则关注全部复平面,而Z变换则是将拉普拉斯的复平面投影到Z平面,将虚轴变为一个圆环。 三、离散小波变换(DWT)的理解由于CWT需要一个连续信号,但是实际采样信号往往是离散的,我们无法直接对实际信号进行CWT。 或许你想,我们对实际采样信号进行插值连续化不就可以使得其连续了吗?是的。将实际采样信号插值连续化之后,我们——人,是可对它进行CWT的。但是,我们也都知道,我们的帮手——计算机,是无法处理连续问题的。计算机只能处理离散问题。如果计算机要进行CWT,就意味着需要计算机做无穷次运算,计算机计算能力再强也是做不到的。 因此,为了使得计算机可以进行小波变换,我们需要引入离散小波变换(DWT)。 3.1 离散小波变换(DWT)定义
经过小波变换后图像会生成低频信息和高频信息。低频信息对应于求均值,高频信息对应于求差值。 均值是局部的平均值,变化缓慢,属于低频信息,存储图片的轮廓信息,近似信息;差值是局部的波动值,变化较快,属于高频信息,存储图片的细节信息,局部信息,另外含有噪音。h(high)是高通滤波器,允许高频信息通过;h(low)是低通滤波器,允许低频信息通过 h(high)是高通滤波器,允许高频信息通过;h(low)是低通滤波器,允许低频信息通过 DWT有很多种实现方式,其中Mallet算法,它是DWT的以一种经典的快速算法,也比较易懂。关于Mallet算法,可见离散小波变换(DWT)的Mallet算法 3.5 离散小波变换(DWT)的应用在小波分析中经常用到近似于细节,近似表示信号的高尺度,即低频信息;细节表示信号的低尺度,即高频信息。 对含有噪声的信号,噪声分量的主要能量集中在小波解的细节分量中。 小结: 在数字图像处理中,需要将连续的小波及其小波变换离散化。一般计算机实现中使用二进制离散处理,将经过这种离散化的小波及其相应的小波变换成为离散小波变换(简称DWT)。实际上,离散小波变换是对连续小波变换的尺度、位移按照2的幂次进行离散化得到的,所以也称之为二进制小波变换。这里要特别注意:DWT并没有将信号f(t)和小波ψ(t)中的时间变量t离散化!这与DFT的概念是非常不一样的!!小波分解的意义就在于能够在不同尺度上对信号进行分解,而且对不同尺度的选择可以根据不同的目标来确定。 四、总结 小波变换可以提取信号的局部特征,即可以知道信号的各个频率分量分别是多少,以及他们都是什么时候出现的(而傅里叶变换只能知道频率分量,短时傅里叶变换尽管可以提取局部变量,但由于其窗口固定,无法满足非稳态信号频率变化的需求);小波变换是傅里叶的“基变换”,将傅里叶变换中无限长的三角函数基换成了有限长的会衰减的小波基;小波可以认为是一个带通滤波器,只允许频率和小波中心频率(经过尺度伸缩后)相近的信号的通过;以morlet小波基函数为例,分析连续小波变换(CWT),morlet小波基函数 = 复三角函数 + 衰减函数。(复三角函数使其能分析频率(和原始信号乘积积分求极大值),衰减函数使其可以定位时间);尺度a是一个很重要的参数,因为它不仅仅能产生一系列中心频率不同的小波基函数(带通滤波器)—对应复三角函数,还可以控制基函数在时域的支撑区间(带通滤波器的带宽)—对应衰减函数,进而控制时间分辨率和频率分辨率;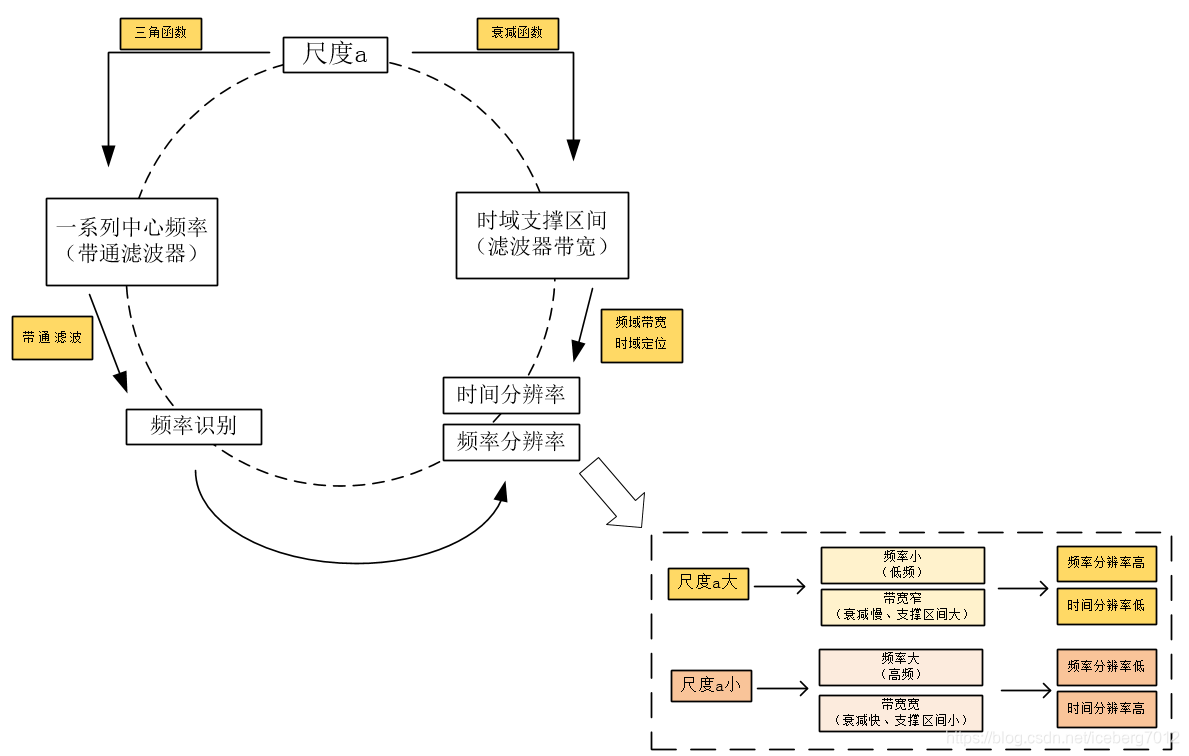 实际上,离散小波变换是对连续小波变换的尺度、位移按照2的幂次进行离散化得到的,所以也称之为二进制小波变换。为了使得计算机可以进行小波变换,我们需要引入离散小波变换(DWT),而Mallet算法是DWT的以一种经典的快速算法,也比较易懂。 实际上,离散小波变换是对连续小波变换的尺度、位移按照2的幂次进行离散化得到的,所以也称之为二进制小波变换。为了使得计算机可以进行小波变换,我们需要引入离散小波变换(DWT),而Mallet算法是DWT的以一种经典的快速算法,也比较易懂。
本文参考来源: 连续小波变换(CWT) 从傅里叶变换进阶到小波变换 DWT(离散小波变换) 连续小波变换、离散小波变换、二进小波变换、离散序列的小波变换、小波包 |
【本文地址】
今日新闻 |
推荐新闻 |
 下面对傅里叶变换与小波变换的优缺点做一个小结,如下:
下面对傅里叶变换与小波变换的优缺点做一个小结,如下:

 当伸缩、平移到这么一种重合情况时,也会相乘得到一个大的值。这时候和傅里叶变换不同的是,这不仅可以知道信号有这样频率的成分,而且知道它在时域上存在的具体位置。而当我们在每个尺度线都平移着和信号乘过一遍后,我们就知道信号在每个位置上都包含哪些频率成分。
当伸缩、平移到这么一种重合情况时,也会相乘得到一个大的值。这时候和傅里叶变换不同的是,这不仅可以知道信号有这样频率的成分,而且知道它在时域上存在的具体位置。而当我们在每个尺度线都平移着和信号乘过一遍后,我们就知道信号在每个位置上都包含哪些频率成分。 傅里叶变换结果:
傅里叶变换结果:  小波变换结果:
小波变换结果:  由此,可进一步说明,傅里叶变换仅能知道信号的频率成分,小波变换不仅能知道信号的频率成分,还能知道各频率成分出现的时刻。
由此,可进一步说明,傅里叶变换仅能知道信号的频率成分,小波变换不仅能知道信号的频率成分,还能知道各频率成分出现的时刻。 衰减的小波时:
衰减的小波时:  以上,就是小波的意义。另外补充几个小波变换与傅里叶变换中的常见问题:
以上,就是小波的意义。另外补充几个小波变换与傅里叶变换中的常见问题: morlet小波的基函数是由复三角函数乘上一个指数衰减函数构成,这里表示中心频率W0。还是先看图一(分别令W0=2,W0=5):
morlet小波的基函数是由复三角函数乘上一个指数衰减函数构成,这里表示中心频率W0。还是先看图一(分别令W0=2,W0=5):  上图左边是基函数时域图像,右边是傅里叶变换图像。可以看到基函数的频率正是其中心频率的值。这里给出morlet小波的傅里叶变换表达式:
上图左边是基函数时域图像,右边是傅里叶变换图像。可以看到基函数的频率正是其中心频率的值。这里给出morlet小波的傅里叶变换表达式:  从表达式也可以看出当频率等于其中心频率W0时,取极大值。这里复三角函数可以辨认频率,衰减函数可以保证其时域的有限支撑。只给一个固定的中心频率可不能辨认信号的频率,同样,基函数只在【-2,2】之间也确定不了时间区间。所以这里的小波基函数需要平移和伸缩 。又是一个公式(按传统,这个变大时前还有一个根号a,但我不讨论这个):
从表达式也可以看出当频率等于其中心频率W0时,取极大值。这里复三角函数可以辨认频率,衰减函数可以保证其时域的有限支撑。只给一个固定的中心频率可不能辨认信号的频率,同样,基函数只在【-2,2】之间也确定不了时间区间。所以这里的小波基函数需要平移和伸缩 。又是一个公式(按传统,这个变大时前还有一个根号a,但我不讨论这个):  于是,给出b=5(平移因子),a=2(尺度变量),即平移5个单位,缩小2倍的morlet小波基函数的图像,见下图二:
于是,给出b=5(平移因子),a=2(尺度变量),即平移5个单位,缩小2倍的morlet小波基函数的图像,见下图二:  相对图一,从时域可以明显看出平移,从频域也很明显看出尺度伸缩。当然从傅里叶变换的性质也可以推断出来。
相对图一,从时域可以明显看出平移,从频域也很明显看出尺度伸缩。当然从傅里叶变换的性质也可以推断出来。 由公式,我们可以看出,连续小波变换的运算是积分,是原始信号与小波基函数乘积后积分的过程,而积分就是一个求和的过程。于是,为什么小波变换能确定信号频率和其对应时间区域?转换为==>为什么小波变换会在原始信号固有的频率上产生极大值?而这极大值对应的区间正好是该频率的时区。
由公式,我们可以看出,连续小波变换的运算是积分,是原始信号与小波基函数乘积后积分的过程,而积分就是一个求和的过程。于是,为什么小波变换能确定信号频率和其对应时间区域?转换为==>为什么小波变换会在原始信号固有的频率上产生极大值?而这极大值对应的区间正好是该频率的时区。 好,到这里你应该就明白了为什么小波变换会在原始信号固有的频率上产生极大值? 因为基函数里包含复三角函数 (欧拉公式,复数与三角函数的转化)。
好,到这里你应该就明白了为什么小波变换会在原始信号固有的频率上产生极大值? 因为基函数里包含复三角函数 (欧拉公式,复数与三角函数的转化)。 再次求其与y乘积积分后的最大值(这个得取模)。很明显,当a=2的时候,也就是小波基函数频率为5的时候,会取的极大值,如图:
再次求其与y乘积积分后的最大值(这个得取模)。很明显,当a=2的时候,也就是小波基函数频率为5的时候,会取的极大值,如图:  小结:
小结: 其对应的小波变换二维时频图(语谱图)如下:
其对应的小波变换二维时频图(语谱图)如下:  由上图,我们可以看出,低频时(频率为4),对应彩色条纹更细,意味着更高的频率分辨率,而条纹区间大概落在【0,2.5】之间,这意味着较低的时间分辨率。同理,高频时,对应更低的频率分辨率和更高的时间分辨率。这是小波最为人知的特性,也是它被称为“数学显微镜”的原因,接下来我们一起探讨下为何小波具有这种特征。
由上图,我们可以看出,低频时(频率为4),对应彩色条纹更细,意味着更高的频率分辨率,而条纹区间大概落在【0,2.5】之间,这意味着较低的时间分辨率。同理,高频时,对应更低的频率分辨率和更高的时间分辨率。这是小波最为人知的特性,也是它被称为“数学显微镜”的原因,接下来我们一起探讨下为何小波具有这种特征。 前面说到,小波就是一个带通滤波器,它只允许频率和自己本身中心频率相近的信号通过。那么这个相近,到底相差多少才叫相近呢?上图,很明显可以看到,不同频率小波基函数在频域的带宽是不一样的,低频时的带宽窄,高频是的带宽要更宽一点。而带宽越窄,意味着小波这个带通滤波器,允许通过的频率越接近小波本身的中心频率,即频率分辨率越高,反之,带宽越宽,对应的频率分辨率越低。(补充:小波带宽与中心频率无关,与尺度a有关,见证明)
前面说到,小波就是一个带通滤波器,它只允许频率和自己本身中心频率相近的信号通过。那么这个相近,到底相差多少才叫相近呢?上图,很明显可以看到,不同频率小波基函数在频域的带宽是不一样的,低频时的带宽窄,高频是的带宽要更宽一点。而带宽越窄,意味着小波这个带通滤波器,允许通过的频率越接近小波本身的中心频率,即频率分辨率越高,反之,带宽越宽,对应的频率分辨率越低。(补充:小波带宽与中心频率无关,与尺度a有关,见证明) 而,它们的时域图像,分别如下图三、图四:
而,它们的时域图像,分别如下图三、图四: 
 两个表达式只在衰减函数的部分有区别,一个有尺度a,另一个没有。看图三中明显看出基函数长度不一,即他们的支撑区间(非零区间)都不一样,这主要是由于衰减函数(exp(-t^ 2/2a^ 2))导致的。于是,我们可以得到,尺度a越大,衰减越慢,支撑区间也就越大,反之,亦然。换句话说,尺度参数a不仅可以用来生成一些列的不同中心频率的基函数,还可以控制基函数在时域的支撑区间。
两个表达式只在衰减函数的部分有区别,一个有尺度a,另一个没有。看图三中明显看出基函数长度不一,即他们的支撑区间(非零区间)都不一样,这主要是由于衰减函数(exp(-t^ 2/2a^ 2))导致的。于是,我们可以得到,尺度a越大,衰减越慢,支撑区间也就越大,反之,亦然。换句话说,尺度参数a不仅可以用来生成一些列的不同中心频率的基函数,还可以控制基函数在时域的支撑区间。
 图五和图六中,图五的时间分辨率肯定更高,因为它的窗口短,时间定位更准,但是正是因为其窗口短,使得其频率分辨率更低。
图五和图六中,图五的时间分辨率肯定更高,因为它的窗口短,时间定位更准,但是正是因为其窗口短,使得其频率分辨率更低。




 A是低频信息,H是水平高频信息,V是垂直高频信息、D是对角高频信息。
A是低频信息,H是水平高频信息,V是垂直高频信息、D是对角高频信息。 

