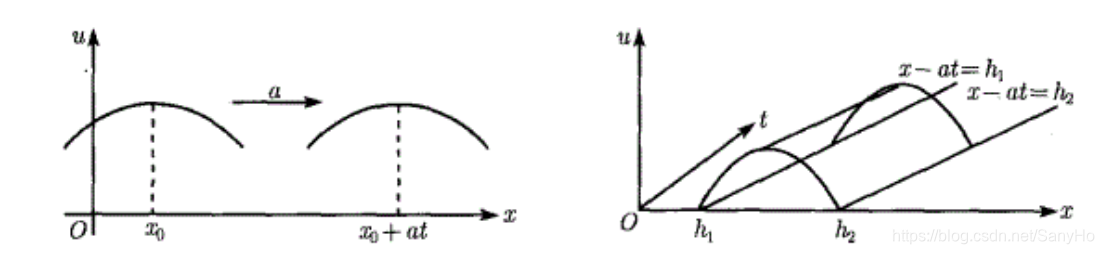
先求通解再确定特解，是求常微分方程定解问题采用的方法，都某些偏微分方程，也能通过积分求出通解，进而确定出满足定解条件的特解。

今有两个自变量的一阶线性偏微分方程。 a ( x , y ) ∂ u ∂ x + b ( x , y ) ∂ u ∂ y + c ( x , y ) u = f ( x , y ) (1) a(x,y)\frac{\partial u}{\partial x}+b(x,y)\frac{\partial u}{\partial y}+c(x,y)u=f(x,y) \tag{1} a(x,y)∂x∂u​+b(x,y)∂y∂u​+c(x,y)u=f(x,y)(1) 其中，系数 a ( x , y ) , b ( x , y ) , c ( x , y ) a(x,y),b(x,y),c(x,y) a(x,y),b(x,y),c(x,y)是平面区域 D ⊂ R 2 D\subset \bold R^2 D⊂R2上的连续函数，且 a ( x , y ) , b ( x , y ) a(x,y),b(x,y) a(x,y),b(x,y)不同时为零， f ( x , y ) f(x,y) f(x,y)在D上连续，称为方程的非齐次项。若 f ( x , y ) ≡ 0 f(x,y)\equiv 0 f(x,y)≡0，方程为齐次的。

思路：将两个自变量的方程化为求一个自变量的方程

情况1：如果在D上， a ( x , y ) ≡ 0 , b ( x , y ) ≠ 0 a(x,y)\equiv 0,b(x,y)\neq 0 a(x,y)≡0,b(x,y)​=0，方程（1）改写为 ∂ u ∂ x + c ( x , y ) b ( x , y ) u = f ( x , y ) b ( x , y ) (2) \frac{\partial u}{\partial x}+\frac{c(x,y)}{b(x,y)}u=\frac{f(x,y)}{b(x,y)} \tag{2} ∂x∂u​+b(x,y)c(x,y)​u=b(x,y)f(x,y)​(2) 利用一阶线性常微分方程的求解方法得其通解。 u ( x , y ) = e x p ( − ∫ c ( x , y ) b ( x , y ) d y ) ⋅ [ ∫ e x p ( ∫ c ( x , y ) b ( x , y ) ) f ( x , y ) b ( x , y ) d y + g ( x ) ] u(x,y)=exp(-\int \frac{c(x,y)}{b(x,y)}dy)·[\int exp(\int \frac{c(x,y)}{b(x,y)})\frac{f(x,y)}{b(x,y)}dy+g(x)] u(x,y)=exp(−∫b(x,y)c(x,y)​dy)⋅[∫exp(∫b(x,y)c(x,y)​)b(x,y)f(x,y)​dy+g(x)] 其中， g ( x ) g(x) g(x)为任意C函数。

情况2：如果在D上， a ( x , y ) b ( x , y ) ≠ 0 a(x,y)b(x,y)\neq 0 a(x,y)b(x,y)​=0，方程（1）不能直接积分求解，试作待定的自变量代换 { ξ = φ ( x , y ) η = ψ ( x , y ) (a) \begin{cases} \xi=\varphi(x,y) \\ \eta=\psi(x,y) \end{cases} \tag{a} {ξ=φ(x,y)η=ψ(x,y)​(a) 要求其雅可比（Jacobi）行列式 J ( φ , ψ ) = ∂ ( φ , ψ ) ∂ ( x , y ) = ∣ ∂ φ ∂ x ∂ φ ∂ y ∂ ψ ∂ x ∂ ψ ∂ y ∣ ≠ 0 J(\varphi,\psi)=\frac{\partial (\varphi,\psi)}{\partial(x,y)}= \begin{vmatrix} \frac{\partial \varphi}{\partial x} & \frac{\partial \varphi}{\partial y} \\ \frac{\partial \psi}{\partial x} & \frac{\partial \psi}{\partial y} \end{vmatrix} \neq 0 J(φ,ψ)=∂(x,y)∂(φ,ψ)​=∣∣∣∣∣​∂x∂φ​∂x∂ψ​​∂y∂φ​∂y∂ψ​​∣∣∣∣∣​​=0 以保证新变量 ξ , η \xi,\eta ξ,η的相互独立性，利用链式法则 ∂ u ∂ x = ∂ u ∂ ξ ∂ ξ ∂ x + ∂ u ∂ η ∂ η ∂ x = ∂ φ ∂ x ∂ u ∂ ξ + ∂ ψ ∂ x ∂ u ∂ η ∂ u ∂ y = ∂ u ∂ ξ ∂ ξ ∂ y + ∂ u ∂ η ∂ η ∂ y = ∂ φ ∂ y ∂ u ∂ ξ + ∂ ψ ∂ y ∂ u ∂ η \frac{\partial u}{\partial x}=\frac{\partial u}{\partial \xi}\frac{\partial \xi}{\partial x}+\frac{\partial u}{\partial \eta}\frac{\partial \eta}{\partial x}=\frac{\partial \varphi}{\partial x}\frac{\partial u}{\partial \xi}+\frac{\partial \psi}{\partial x}\frac{\partial u}{\partial \eta} \\ \frac{\partial u}{\partial y}=\frac{\partial u}{\partial \xi}\frac{\partial \xi}{\partial y}+\frac{\partial u}{\partial \eta}\frac{\partial \eta}{\partial y}=\frac{\partial \varphi}{\partial y}\frac{\partial u}{\partial \xi}+\frac{\partial \psi}{\partial y}\frac{\partial u}{\partial \eta} ∂x∂u​=∂ξ∂u​∂x∂ξ​+∂η∂u​∂x∂η​=∂x∂φ​∂ξ∂u​+∂x∂ψ​∂η∂u​∂y∂u​=∂ξ∂u​∂y∂ξ​+∂η∂u​∂y∂η​=∂y∂φ​∂ξ∂u​+∂y∂ψ​∂η∂u​ u = u ( x , y ) u=u(x,y) u=u(x,y)的方程（1）变为 u = u ( x ( ξ , η ) , y ( ξ , η ) ) = u ( ξ , η ) u=u(x(\xi,\eta),y(\xi,\eta))=u(\xi,\eta) u=u(x(ξ,η),y(ξ,η))=u(ξ,η)的新方程 ( a ∂ φ ∂ x + b ∂ φ ∂ y ) ∂ u ∂ ξ + ( a ∂ ψ ∂ x + b ∂ ψ ∂ y ) ∂ u ∂ η + c u = f (3) (a\frac{\partial \varphi}{\partial x}+b\frac{\partial \varphi}{\partial y})\frac{\partial u}{\partial \xi}+(a\frac{\partial \psi}{\partial x}+b\frac{\partial \psi}{\partial y})\frac{\partial u}{\partial \eta}+cu=f \tag{3} (a∂x∂φ​+b∂y∂φ​)∂ξ∂u​+(a∂x∂ψ​+b∂y∂ψ​)∂η∂u​+cu=f(3) 若取 ξ = φ ( x , y ) \xi=\varphi(x,y) ξ=φ(x,y)是齐次一阶线性偏微分方程 a ( x , y ) ∂ φ ∂ x + b ( x , y ) ∂ φ ∂ y = 0 (4) a(x,y)\frac{\partial \varphi}{\partial x}+b(x,y)\frac{\partial \varphi}{\partial y}=0 \tag{4} a(x,y)∂x∂φ​+b(x,y)∂y∂φ​=0(4) 的解，则新方程（3）称为（2）型的方程 ( a ∂ ψ ∂ x + b ∂ ψ ∂ y ) ∂ u ∂ η + c u = f (b) (a\frac{\partial \psi}{\partial x}+b\frac{\partial \psi}{\partial y})\frac{\partial u}{\partial \eta}+cu=f \tag{b} (a∂x∂ψ​+b∂y∂ψ​)∂η∂u​+cu=f(b) 对 η \eta η积分便可求出通解。

以下求解一阶线性偏微分方程（4），它的解对应与相应的常微分方程 a ( x , y ) d y − b ( x , y ) d x = 0 (5) a(x,y)dy-b(x,y)dx=0 \tag{5} a(x,y)dy−b(x,y)dx=0(5) 亦即 d x a ( x , y ) = d y b ( x , y ) (6) \frac{dx}{a(x,y)}=\frac{dy}{b(x,y)} \tag{6} a(x,y)dx​=b(x,y)dy​(6) 的解之间存在确定的关系。

定理：若 φ ( x , y ) = h \varphi(x,y)=h φ(x,y)=h（常数）是一阶常微分方程（5）在区域D内的隐式通解（积分曲线族），则 ξ = φ ( x , t ) \xi=\varphi(x,t) ξ=φ(x,t)是一阶线性偏微分方程（4）在区域D上的一个解。

证明：设 φ ( x , y ) = h \varphi(x,y)=h φ(x,y)=h是方程（5）在D内的隐式通解，则过D内一点 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)有一条积分曲线 Γ 0 : φ ( x , y ) = φ ( x 0 , y 0 ) = h 0 \Gamma_0:\varphi(x,y)=\varphi(x_0,y_0)=h_0 Γ0​:φ(x,y)=φ(x0​,y0​)=h0​，此隐式解满足方程 d x a ( x , y ) = d y b ( x , y ) \frac{dx}{a(x,y)}=\frac{dy}{b(x,y)} a(x,y)dx​=b(x,y)dy​ 又沿此积分曲线 Γ 0 \Gamma_0 Γ0​，有 ∂ φ ∂ x d x + ∂ φ ∂ y d y = 0 \frac{\partial \varphi}{\partial x}dx+\frac{\partial \varphi}{\partial y}dy=0 ∂x∂φ​dx+∂y∂φ​dy=0 故在 Γ 0 \Gamma_0 Γ0​上，有 a ( x , y ) ∂ φ ∂ x + b ( x , y ) ∂ φ ∂ y = 0 a(x,y)\frac{\partial \varphi}{\partial x}+b(x,y)\frac{\partial \varphi}{\partial y}=0 a(x,y)∂x∂φ​+b(x,y)∂y∂φ​=0 由于 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)是D内任意一点，故 ξ = φ ( x , y ) \xi=\varphi(x,y) ξ=φ(x,y)是一阶线性偏微分方程（4）在D上的解。

定题的逆命题也成立。

由常微分方程理论，一阶常微分方程（5）在区域D内存在且仅存在一族独立的积分曲线。如果求出了方程（5）的积分曲线族 φ ( x , y ) = h \varphi(x,y)=h φ(x,y)=h，再任取函数 ψ ( x , y ) \psi(x,y) ψ(x,y)，使在D上 J ( φ , ψ ) ≠ 0 J(\varphi,\psi)\neq 0 J(φ,ψ)​=0，以此 φ \varphi φ和 ψ \psi ψ作变量代换（a）式，一阶线性偏微分（1）便可化为可积分求通解的方程（b）。

特别地，当 c ( x , y ) = f ( x , y ) ≡ 0 c(x,y)=f(x,y)\equiv 0 c(x,y)=f(x,y)≡0时，方程（1）即为方程（4），相应的新方程（b）为 ∂ u ∂ η = 0 \frac{\partial u}{\partial \eta}=0 ∂η∂u​=0，其通解为 u = g ( ξ ) , g ( ξ ) u=g(\xi),g(\xi) u=g(ξ),g(ξ)为任意C函数。代回原自变量，得方程 a ( x , y ) ∂ u ∂ x + b ( x , y ) ∂ u ∂ y = 0 a(x,y)\frac{\partial u}{\partial x}+b(x,y)\frac{\partial u}{\partial y}=0 a(x,y)∂x∂u​+b(x,y)∂y∂u​=0 的通解 u = g ( φ ( x , y ) ) u=g(\varphi(x,y)) u=g(φ(x,y))。这里， φ ( x , y ) = h \varphi(x,y)=h φ(x,y)=h是常微分方程（5）的隐式通解， g ( ξ ) g(\xi) g(ξ)是任意C函数。

如果给定u在某一曲线 Γ : γ ( x , y ) = d \Gamma:\gamma(x,y)=d Γ:γ(x,y)=d上的值，则需求解定解问题 { a ( x , y ) ∂ u ∂ x + b ( x , y ) ∂ u ∂ y = 0 u ∣ γ ( x , y ) = d = θ ( y ) \begin{cases} a(x,y)\frac{\partial u}{\partial x}+b(x,y)\frac{\partial u}{\partial y}=0 \\ u|_{\gamma(x,y)=d}=\theta(y) \end{cases} {a(x,y)∂x∂u​+b(x,y)∂y∂u​=0u∣γ(x,y)=d​=θ(y)​ 用定解条件定出通解中的任意函数 g ( ξ ) g(\xi) g(ξ)即可。

这种求解定解问题的方法称之为通解法。常微分方程（5）或等价的方程（6）称为一阶线性偏微分方程（1）的特征方程，其积分曲线称之为特征曲线。

例1：求解右行单波方程的初值问题 { ∂ u ∂ t + a ∂ u ∂ x = 0 , t > 0 , − ∞ < x < + ∞ u ∣ t = 0 = φ ( x ) \begin{cases} \frac{\partial u}{\partial t}+a \frac{\partial u}{\partial x}=0,\quad t>0,-\infty0为常数。

解：特征方程 d x − a d t = 0 dx-adt=0 dx−adt=0，特征线族为 x − a t = h x-at=h x−at=h。

令 ξ = x − a t , η = x \xi=x-at, \eta=x ξ=x−at,η=x，则方程化为 ∂ u ∂ η = 0 \frac{\partial u}{\partial \eta}=0 ∂η∂u​=0 对 η \eta η积分得通解 u = g ( ξ ) = g ( x − a t ) u=g(\xi)=g(x-at) u=g(ξ)=g(x−at)，其中， g ( ξ ) g(\xi) g(ξ)是任意C函数。由初始条件 u ∣ t = 0 = g ( x ) = φ ( x ) u|_{t=0}=g(x)=\varphi(x) u∣t=0​=g(x)=φ(x) 得该初值问题的解 u ( t , x ) = φ ( x − a t ) u(t,x)=\varphi(x-at) u(t,x)=φ(x−at)

在 ( x , u ) (x,u) (x,u)平面上看（图1.3.1）， t = 0 t=0 t=0时 u = φ ( x ) u=\varphi(x) u=φ(x)，对每个固定时刻 t > 0 ， u = φ ( x − a t ) ] t>0，u=\varphi(x-at)] t>0，u=φ(x−at)]，其图形相当于曲线 u = φ ( x ) u=\varphi(x) u=φ(x)向右移动了 a t at at，波形的传播速度为 a a a。称这样的解为右行波解。

在 ( x , t , u ) (x,t,u) (x,t,u)空间看（图1.3.2），波形沿特征线传播。在特征线 x − a t = h x-at=h x−at=h上， u = φ ( x − a t ) = φ ( h ) u=\varphi(x-at)=\varphi(h) u=φ(x−at)=φ(h)，故当观察者沿某条特征线前行时，看到的波形始终不变。如果初始扰动 φ ( x ) \varphi(x) φ(x)只发生在区间 h 1 ≤ x ≤ h 2 h_1\leq x\leq h_2 h1​≤x≤h2​内，则这个扰动沿着 ( x , t ) (x,t) (x,t)平面上的特征条形域 h 1 ≤ x − a t ≤ h 2 h_1\leq x-at\leq h_2 h1​≤x−at≤h2​传播。

本例中初始条件给在非特征线的直线 t = 0 t=0 t=0上，从通解可唯一确定特解。如果初始条件给在一条特征线 x − a t = h 0 x-at=h_0 x−at=h0​上，初始条件 u ∣ x − a t = h 0 = g ( x − a t ) ∣ x − a t = h 0 = g ( h 0 ) = φ ( x ) u|_{x-at=h_0}=g(x-at)|_{x-at=h_0}=g(h_0)=\varphi(x) u∣x−at=h0​​=g(x−at)∣x−at=h0​​=g(h0​)=φ(x)，当 φ ( x ) \varphi(x) φ(x)为非常值函数时无解，当 φ ( x ) \varphi(x) φ(x)为常数 φ 0 \varphi_0 φ0​时有无穷多个解 g ( ξ ) g(\xi) g(ξ)，只要 g ( h 0 ) = φ 0 g(h_0)=\varphi_0 g(h0​)=φ0​。

对于左行单波方程 ∂ u ∂ t − a ∂ u ∂ x = 0 \frac{\partial u}{\partial t}-a\frac{\partial u}{\partial x}=0 ∂t∂u​−a∂x∂u​=0，同样可求得其通解为左行波 u = g ( x + a t ) u=g(x+at) u=g(x+at)， g g g为任意 C 1 C^1 C1函数（一阶连续导数）。