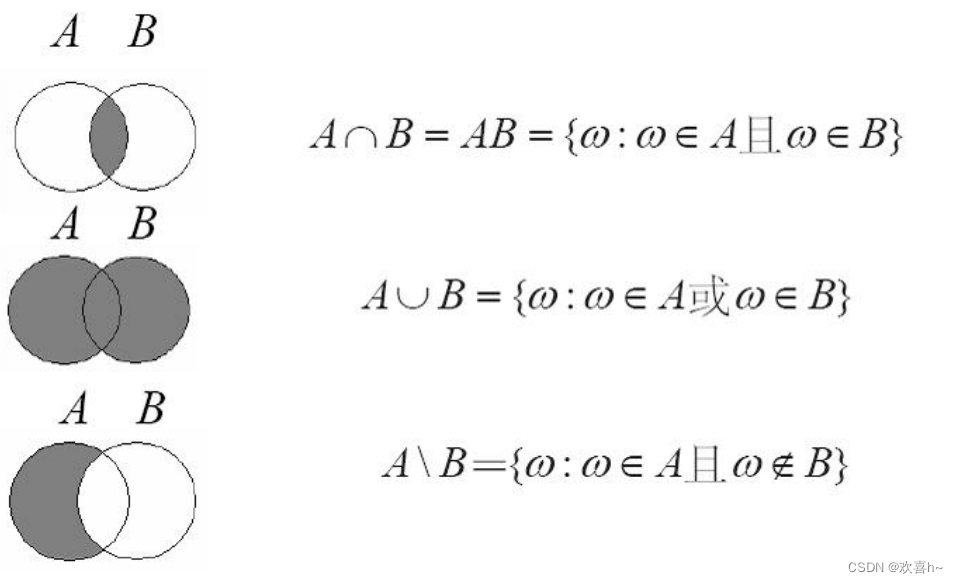随机过程复习（一）概率论基础与随机过程概述

您所在的位置：网站首页 › 一维随机变量的分布函数是单调不减的连续函数 › 随机过程复习（一）概率论基础与随机过程概述

随机过程复习（一）概率论基础与随机过程概述

2024-07-15 00:00| 来源: 网络整理| 查看: 265

1. 概率的公理化定义 1.1 概念随机现象：在一定条件下，可能出现也可能不会出现的现象。随机试验：

(1)试验可在相同条件下重复进行；

(2)每次试验只有一个结果出现并且结果不可预知；

(3)每次试验所有可能出现的结果已知。

所有试验的可能结果组成的集合称为样本空间，记成 $\Omega$ . $\Omega$ 中的元素 $\omega$ 称为样本点. $\Omega$ 的子集A称为随机事件或简称事件. 1.2 随机事件的关系运算

1.3 概率的直观定义 1.3.1 古典概型

称定义在样本空间 $\Omega$ 上的概型为古典概型，如果：

样本空间 $\Omega$ 是有限集；每个样本 $\omega$ 的出现是等可能的。 $A\subset\Omega,P(A)=\frac{\mu(A)}{\mu(\Omega)}$ 1.3.2 几何概型

称定义在样本空间 $\Omega$ 上的概型为几何概型，如果：

样本空间 $\Omega$ 是无限集；每个样本 $\omega$ 的出现时等可能的。 $A\subset\Omega,P(A)=\frac{\mu(A)}{\mu(\Omega)}$ 1.3.3 概率定义

设 $(\Omega, \mathcal{F})$ 为可测空间，P是定义在 $\mathcal{F}$ 上的实值函数，若满足：

$P(A)\geqslant 0, \forall A\in\mathcal{F}$ （非负性） $P(\Omega)=1$ （归一性）若 $A_i\in \mathcal{F},i=1,2,...,$ 且 $A_iA_j=\varnothing ,\forall i\neq j$ ，有

$P(\bigcup_{i=1}^\infty A_i)=\sum_{i=1}^\infty P(A_i)$ （可列可加性）

称P为可测空间 $(\Omega, \mathcal{F})$ 上的概率测度，简称概率。称 $(\Omega, \mathcal{F},P)$ 为概率空间，称 $\mathcal{F}$ 为事件域。若 $A\in\mathcal{F}$ ，称A为随机事件或时间，称P(A)为事件的概率。

概率的性质

$P(\varnothing )=0,P(A^C)=1-P(A)$ 若 $A\subset B$ ，则 $P(A)\leqslant P(B)$ 若 $A_1,A_2,...,A_n$ 互不相容，则 $P(\bigcup_{i=1}^nA_i)=\sum_{i=1}^nP(A_i)$ （有限可加性）对任意两个时间A及B，有

$P(A\cup B)\quad=\quad P(A)+P(B)-P(AB)$

$P(A-B)^2=2P(A)-P(AB)$

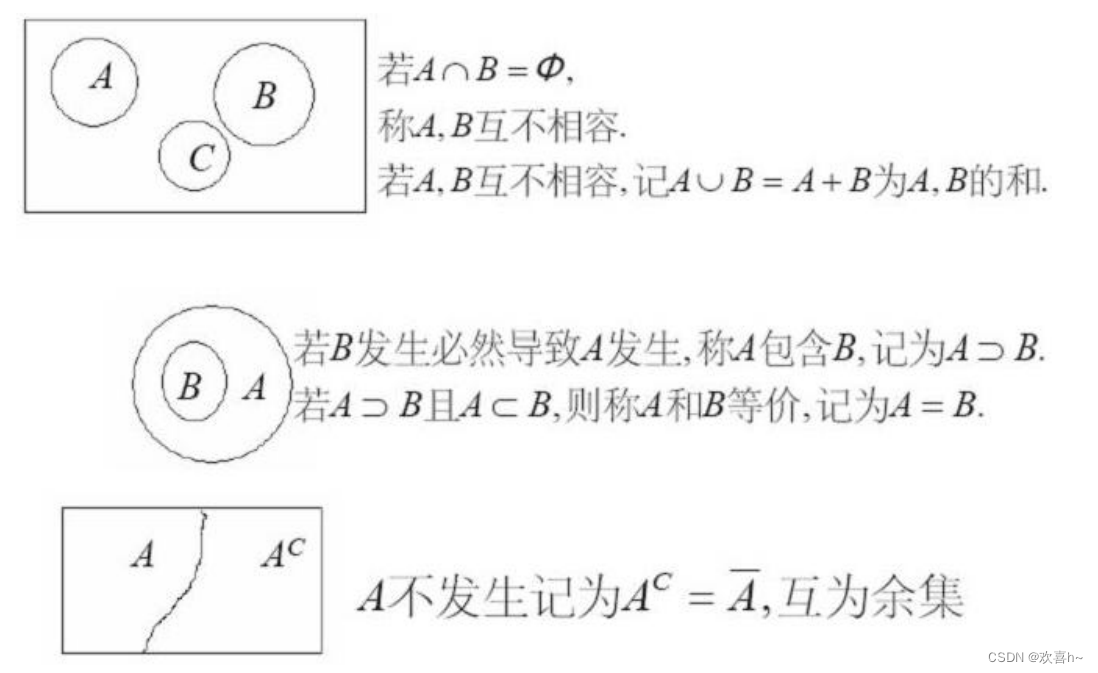
5.（若当(Jordan)公式），对任意 $A_1,A_2,...,A_n$ ，有

$\begin{aligned} P(\bigcup_{i=1}^nA_i)& \sum_{i=1}P(A_i)-\sum_{1\leqslant ij\leqslant n}P(A_iA_j)+\sum_{1\leqslant ijk\leqslant n}P(A_iA_jA_k) \\ &-\cdots+(-1)^{n+1}P(A_1A_2\cdots A_n) \\ &P(\bigcup_{i=1}^nA_i)\leqslant\sum_{i=1}^nP(A_i) \end{aligned}$

1.4 条件概率

设 $(\Omega, \mathcal{F},P)$ 为一概率空间， $A,B\in \mathcal{F}$ ，且P(B)>0，则称

$P(A|B)=\frac{P(AB)}{P(B)}$

为在事件B发生的条件下，事件A发生的条件概率。

几个重要的公式：

乘法公式

若 $A_1,A_2,...,A_n\in\mathcal{F}$ ，且 $P(A_1...A_{n-1})0$ 则

$P(A_1A_2\cdots A_n)=P(A_1)P(A_2|A_1)P(A_3|A_1A_2)\cdots P(A_n|A_1\cdots A_{n-1})$

全概率公式

若 $A,B_1,...,B_n\in\mathcal{F}$ ， $P(B_1),...,P(B_n)0$ ，且 $B_1,...,B_n$ 两两互不相容， $A\subset\bigcup_{i=1}^nB_i$ ，则

$P(A)=\sum_{i=1}^nP(B_i)P(A|B_i)$

贝叶斯公式

若 $A,B_1,...,B_n\in\mathcal{F}$ ， $P(A),P(B_1),...,P(B_n)0$ ，且 $B_1,...,B_n$ 两两互补相容， $A\subset\bigcup_{i=1}^nB_i$ ，则

$P(B_i|A)=\frac{P(B_i)P(A|B_i)}{\sum_{j=1}^nP(B_j)P(A|B_j)}\quad(i=1,2,\cdots,n)$

2. 随机变量与数字特征 2.1 随机变量的定义

设 $(\Omega, \mathcal{F},P)$ 为一概率空间。 $X=X(\omega)$ 是定义在 $\Omega$ 上的单值实函数。若对任意实数X，总有 $\{\omega:X(\omega)\geqslant x\}\in\mathcal{F}$ ,则称 $X(\omega)$ 是 $\mathcal{F}$ 上的随机变量，简记为随机变量X。称

$F(x)=P\{X\leqslant x\}\quad(x\in\mathbb{R})$

为随机变量X的分布函数。

2.2 示性函数

2.3 分布函数的性质 F(x)是单调不减的，即当 $x_1x_2$ 时，有 $F(x_1)\leqslant F(x_2)$ F(x)是右连续的，即 $F(x+0)=F(x)$ $F(-\infty)=\lim_{x\to-\infty}F(x)=0,F(\infty)=\lim_{x\to\infty}F(x)=1.$

离散型随机变量和连续性随机变量

若随机变量X的可能取值的全体是一有限集或可数集，则称X是离散型随机变量。

其概率分布用如下分布律描述：

$p_k=P\{X=x_k\}\quad(k=1,2,\cdots)$

其分布函数为

$F(x)=\sum_{x_k\leqslant x}p_k$

连续性随机变量X的概率分布常用概率密度f(x)描述，其分布函数为

$F(x)=\int_{-\infty}^xf(t)\mathrm{d}t$

显然，对连续型随机变量， $F'(x)=f(x)$ .

2.4 几种常见分布

（1）退化分布

若随机变量X只取常数c，即 $P\{X=c\}=1$ ，则X并不随机，但把它看做随机变量的退化情况更为方便，此时称为退化分布，又称单点分布。

（2）伯努利分布

在一次试验中，设事件A出现的概率为p，不出现的概率为1-p，若以X记事件A出现的次数，则X的取值仅为0,1，其对应的概率为

$P\{X=k\}=p^k(1-p)^{1-k}\quad(k=0,1)$

这个分布称为伯努利分布，又称为两点分布。

（3）二项分布

在n重伯努利试验中，设事件A在每次试验中出现的概率均为p，以X记在n次试验中事件A出现的次数，则X的可能取值为0,1,...,n，其对应的概率为

$\left.P\{X=k\}=\left(\begin{array}{c}n\\k\end{array}\right.\right)p^k(1-p)^{n-k}\quad(k=0,1,\cdots,n)$

称为以n和p为参数的二项分布，简记为X~B(n,p)。

（4）泊松分布

若随机变量X可取一切非负整数值，并且

$P\{X=k\}=\frac{\lambda^k}{k!}\mathrm{e}^{-\lambda}\quad(k=0,1,2,\cdots;\lambda0)$

称X服从泊松分布，记为X~P( $\lambda$ )

（5）几何分布

在伯努利试验序列中，设事件A在每次试验中出现的概率均为p，以X记事件A首次出现的实验次数，则X的可能取值为1,2,...，其对应的概率为

$P\{X=k\}=p(1-p)^{k-1}\quad(k=1,2,\cdots)$

称为几何分布。

（6）帕斯卡分布

在伯努利试验序列中，设事件A在每次实验中出现的概率均为p，以X记时间A第r次出现的试验次数，则X的可能取值为r,r+1,...,其对应的概率为

$\left.P\{X=k\}=\left(\begin{array}{c}k-1\\r-1\end{array}\right.\right)p^r(1-p)^{k-r}\quad(k=r,r+1\cdots)$

称为帕斯卡分布。

（7）离散均匀分布

如果分布律为

$p_k=\frac1n\quad(k=1,2,\cdots,n)$

则称为离散均匀分布。

（8）连续均匀分布

如果X的密度函数为

$\left.f(x)=\left\{\begin{array}{cc}\frac1{b-a}&\quad(a\leqslant x\leqslant b)\\0&\quad (else)\end{array}\right.\right.$

则称X为区间[a,b]上的均匀分布。

（9）正态分布

如果密度函数为

$f(x)=\frac1{\sigma\sqrt{2\pi}}\cdot\exp\{-(x-\mu)^2/2\sigma^2\}\quad(x\in\mathbb{R})$

则称为参数为 $\mu, \sigma^2$ 的正态分布，也称为高斯分布，记为 $X\sim N(\mu, \sigma^2)$

（10）指数分布

如果密度函数为

$\left.f(x)=\left\{\begin{array}{cc}\lambda\mathrm{e}^{-\lambda x}&\quad(x\geqslant0)\\0&\quad(x0)\end{array}\right.\right.$

则称为指数分布。

2.5 数字特征

（1）数学期望

离散型随机变量： $EX=\sum_{k=1}^\infty x_kp_k$

连续型随机变量： $EX=\int_{-\infty}^\infty xf(x)\mathrm{d}x$

一般形式： $EX=\int_{-\infty}^\infty x\mathrm{d}F(x)$

（2）方差： $DX=:E(X-EX)^2=EX^2-(EX)^2$

（3）协方差： $\mathrm{cov}(X,Y)=:E[(X-EX)(Y-EY)]=E(XY)-(EX)(EY)$

（4）相关系数： $\rho(X,Y)=\frac{\mathrm{cov}(X,Y)}{\sigma_X\sigma_Y}$

（5）k阶矩： $E(X^k)=\int_{-\infty}^\infty x^k\mathrm{d}F_X(x)\mathrm{~}(k\geqslant1)$

2.6 几个重要的不等式

（1）施瓦兹不等式：若随机变量X,Y的二阶矩存在，则

$|E(XY)|^2\leqslant E(X^2)E(Y^2)$

特别地，有

$\lvert\operatorname{cov}(X,Y)\rvert^2\leqslant\sigma_X^2\sigma_Y^2\quad(\lvert\rho(X,Y)\rvert\leqslant1)$

（2）切比雪夫不等式：对于任一随机变量X，若EX与DX均存在，则对于任意 $\varepsilon 0$ ，恒有

$P\{|X-EX|\geqslant\varepsilon\}\leqslant\frac{dX}{\varepsilon^2}$

或

$P\{|X-EX|\varepsilon\}\geqslant1-\frac{dX}{\varepsilon^2}$

（3）詹森不等式：若g(`)是R上一个凸函数，即 $\forall \alpha \in (0,1)$ 和 $\forall x,y\in \mathbb{R}$ ，有

$g(\alpha x+(1-\alpha)y)\leqslant\alpha g(x)+(1-\alpha)g(y)$

则

$g(EX)\leqslant E[g(X)]$

（4）马尔可夫不等式：设X是样本空间 $\Omega$ 上的非负随机变量且有有限期望，则对于 $\varepsilon 0$ ，有

$P(X\geqslant\varepsilon)\leqslant\frac{EX}\varepsilon$

3. 条件数学期望 3.1 离散型随机变量的条件数学期望

设X,Y为两个离散型随机变量，其联合分布律为 $P(X=x_i,Y=y_j)=p_{ij}\geqslant 0,\sum_i\sum_jp_{ij}=1$ ，若 $P(Y=y_j)=\sum_i p_{ij}=:p_{.j}0$ ，称

$P(X=x_i|Y=y_j)=P(X=x_i,Y=y_j)/P(Y=y_j)=p_{ij}/p_{.j}$

为给定 $Y=y_j$ 时，X的条件分布律。

称

$E(X|Y=y_j)=:\sum_ix_iP(X=x_i|Y=y_j)$

为给定 $Y=y_j$ 时，X的条件数学期望。

显然， $E(X|Y=y_j)$ 的值是依赖于 $Y=y_j$ 。

X关于Y的条件数学期望E(X|Y)定义为

$E(X|Y)=:\sum_jE(X|Y=y_j)I_{(Y=y_j)}(\omega)$

其中

$\left.I_{\{Y=y_j\}}(\omega)=I_{B_j}(\omega)=\left\{\begin{array}{ll}1&\quad(\omega\in B_j=\{\omega:Y(\omega)=y_j\})\\0&\quad(\omega\notin B_j=\{\omega:Y(\omega)=y_j\})\end{array}\right.\right.$

上式称为E(X|Y)的示性函数表达式。

由于随机变量E(X|Y)是随机变量Y的函数，故它的数学期望为：

$E(E(X|Y))=\sum_jE(X|Y=y_j)P(Y=y_j)$

3.2 连续型随机变量的条件数学期望

设X,Y均为连续型随机变量，(X,Y)的联合概率密度函数为f(x,y)，Y的概率密度函数为 $f_Y(y)=\int_{-\infty}^\infty f(x,y)\mathrm{d}x$ 。设 $f_Y(y)0,E|X|\infty$ ，给定Y=y，X的条件概率密度函数为

$f_{X|Y=y}(x|y)=\frac{f(x,y)}{f_Y(y)}$

条件分布函数为

$F_{X|Y=y}(x|y)=P(X\leqslant x|Y=y)=\int_{-\infty}^x\frac{f(u,y)}{f_Y(y)}\mathrm{d}u$

条件数学期望为

$E(X|Y=y)=\int_{-\infty}^\infty xf_{X|Y=y}(x|y)\mathrm{d}x=\int_{-\infty}^\infty x\frac{f(x,y)}{f_Y(y)}\mathrm{d}x$

EX=E{E(X|Y)}可看作数学期望形式的全概率公式。

求条件数学期望的一般步骤：

先写出固定条件（如 $Y=y_j$ ）情况下X的条件分布律或条件密度函数；根据条件数学期望的定义，通过求和或积分得到给定条件下的数学期望；若Y为连续型随机变量，则将y替换为随机变量Y即可。

4. 随机过程的基本概念

设对每一个参数 $t\in T$ ， $X(t,\omega)$ 是一个随机变量，称随机变量族 $X_T=\{X(t,\omega), t\in T\}$ 为随机过程。其中， $T\subset \mathbb{R}$ 是一个实数集，称为指标集。

从数学观点来看，随机过程 $\{X(t,\omega), t\in T\}$ 是定义在 $T\times \Omega$ 上的二元函数。当t固定时， $X(t,\omega)$ 是定义在样本空间 $\Omega$ 上的函数，即为一随机变量。固定 $\omega$ 时， $X(t,\omega)$ 是定义在T上的普通函数，称为随机过程的样本函数或轨道。当t, $\omega$ 都固定是， $X(t,\omega)$ 就是一个数值，称为随机过程的一个状态。 $X(t,\omega)$ 可能取值的全体所构成的集合称为状态空间，记作S，S中的元素称为状态。

5. 随机过程有限维分布与数字特征

一般来说，对任意给定的 $t_1,...,t_n\in T, (X(t_1),...,X(t_n))$ 是一个n维随机向量，称其联合分布函数

$F_{t_1,\cdots,t_n}(x_1,\cdots,x_n)=P\{X(t_1)\leqslant x_1,\cdots,X(t_n)\leqslant x_n\}$

为随机过程的n维分布函数，简称n维分布。

设 $\{X(t,\omega), t\in T\}$ 是概率空间 $(\Omega, \mathcal{F},P)$ 上的随机过程，对任意 $t\in T$ ，称随机变量X(t)的分布函数 $F_t(x)=P\{X\leqslant x\}$ 为随机过程的一维分布函数，简称一维分布。称X(t)的期望E[X(t)]为随机过程的均值函数，记为 $\mu_X(t)$ ；称X(t)的方差var[X(t)]为随机过程的方差函数，记为 $\sigma_X^2(t)$ ;称方差函数的开方为随机过程的标准差函数，记为 $\sigma_X(t)$ 。

设 $\{X(t,\omega), t\in T\}$ 是某概率空间 $(\Omega, \mathcal{F},P)$ 上的随机过程，对任意两个不同的 $t_1,t_2\in T$ ，称上式所定义的 $F_{t_1,t_2}(x_1,x_2)$ 为随机过程 $\{X(t,\omega), t\in T\}$ 在两个不同时刻 $t_1,t_2$ 的联合二维分布，简称二维分布。称 $E[X(t_1),X(t_2)]$ 为随机过程的自相关函数，简称相关函数，记为 $R_X(t_1,t_2)$ .称

$\begin{aligned} \operatorname{cov}[X(t_1),X(t_2)]& =2E\{[X(t_1)-\mu_X(t_1)][X(t_2)-\mu_X(t_2)]\} \\ &=2E[X(t_1)X(t_2)]-\mu_X(t_1)\mu_X(t_2) \end{aligned}$

为随机过程的协方差函数，记为 $C_X(t_1,t_2)$ .

6. 随机过程的分类

（1）正态过程

设 $\{X(t), t\in T\}$ 是随机过程，若对任意正整数n和 $t_1,t_2,...,t_n\in T$ ， $(X(t_1),X(t_2),...,X(t_n))$ 是n维正态随机变量，则称 $\{X(t,\omega), t\in T\}$ 是正态过程或高斯过程。

（2）维纳过程

随机过程{W(t), t≥0}为维纳过程，若它满足以下三个性质：

每一个增量W(t+s)-W(s)都为正态分布，且均值为 $\mu t$ ，方差为 $\sigma^2t$ ；对任意的 $t_1t_2...t_n$ ，增量 $W(t_2)-W(t_1),...,W(t_n)-W(t_{n-1})$ 独立并服从正态分布；W(0)=0并且W(t)的轨道连续。

（3）平稳过程

设 $\{X(t), t\in T\}$ 为随机过程，若对任意正整数n，任意h>0，当 $t_1,...,t_n\in T, t_1+h, ..., t_n+h\in T$ 时，均有随机向量 $(X(t_1+h),...,X(t_n+h))$ 与 $(X(t_1),...,X(t_n))$ 有相同的联合分布，记为

$(X(t_1+h),\cdots,X(t_n+h))\overset{d}{\operatorname*{=}}(X(t_1),\cdots,X(t_n))$

则称 $\{X(t), t\in T\}$ 为严平稳过程。

若随机过程 $\{X(t), t\in T\}$ 的二阶矩存在，且对任意 $t\in T, E[X(t)]=\mu$ （常数），对任意 $t,t+h\in T,C_X(t,t+h)=C_X(h),h\geqslant 0$ ,则称 $\{X(t), t\in T\}$ 为宽平稳过程或协方差平稳过程。

（4）独立增量过程

设 $\{X(t), t\in T\}$ 为随机过程，若对任意大于等于3的正整数n，任意 $t_1t_2...t_n$ ， $t_1,t_2,...,t_n\in T$ ，随机变量 $X(t_2)-X(t_1), ..., X(t_n)-X(t_{n-1})$ 相互独立，则称 $\{X(t), t\in T\}$ 为独立增量过程。若对任意 $t_1,t_2\in T$ 和任意h>0， $t_1+h, t_2+h\in T$ ，均有

$X(t_1+h)-X(t_1)=:X(t_2+h)-X(t_2)$

则称 $\{X(t), t\in T\}$ 为平稳增量过程。

（5）计数过程

计数过程又称为点过程，设有一随机过程 $\{N(A),A\subset T\}$ ，若N(A)表示集合A中“事件”发生的次数，即它满足：

对 $\forall A\subset T, N(A)$ 是一取值非负整数的随机变量 $(N(\varnothing )=0)$ '对 $\forall A_1,A_2\subset T$ ，若 $A_1A_2=\varnothing$ ，对每一个样本有 $N(A_1\cup A_2)=N(A_1)+N(A_2)$ ，则称 $\{N(A),A\subset T\}$ 为计数过程。

（6）泊松过程

对任意t≥0，若N(t)表示时间段[0,t]内事件A发生的次数，且满足如下三个条件：

N(0)=0;{N(t), t≥0}为独立增量过程；对任意的t≥0,s≥0，N(s+t)-N(s)服从参数为 $\lambda t$ 的泊松分布，则称{N(t), t≥0}是强度为 $\lambda$ 的泊松过程。

（7）马尔可夫过程

设 $\{X(t), t\in T\}$ 为随机过程，其状态空间为S。若对任意正整数n及 $t_1t_2...t_n$ ， $t_1,t_2,...,t_n\in T$ ，任意 $x_1,...,x_{n-1},x_n\in S$ ，其条件分布满足：

$\begin{aligned}\mathsf{P}\{X(t_n)\leqslant x_n|X(t_{n-1})=x_{n-1},\cdots,X(t_1)=x_1\}\\=\quad\mathsf{P}\{X(t_n)\leqslant x_n|X(t_{n-1})=x_{n-1}\}\end{aligned}$

则称 $\{X(t), t\in T\}$ 为马尔可夫过程。

（8）鞅

若对 $\forall t\in T,E|X(t)\infty$ ，且对 $t_1t_2...t_nt_{n+1}$ ，有

$E(X(t_{n+1})|X(t_1),X(t_2),\cdots,X(t_n))=X(t_n)$

则称 $\{X(t), t\in T\}$ 为鞅。

【本文地址】

随机过程复习（一）概率论基础与随机过程概述

随机过程复习（一）概率论基础与随机过程概述

今日新闻

推荐新闻