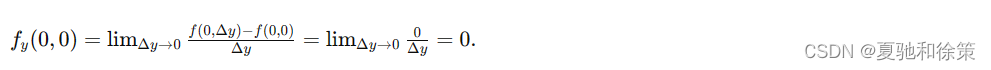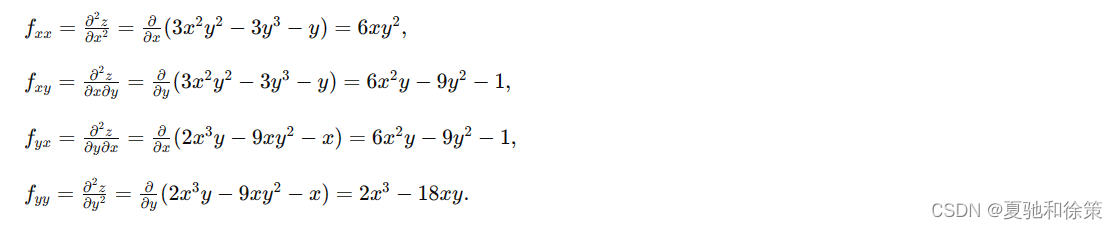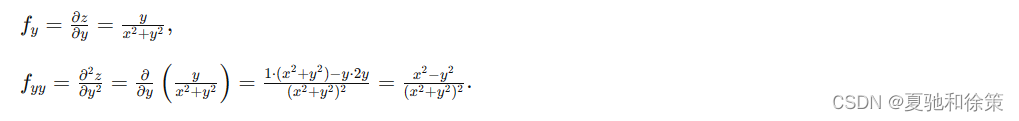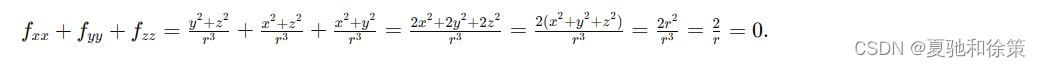在研究一元函数时，我们从研究函数的变化率引入了导数的概念。对于多元函数同样需要讨论它的变化率。但多元函数的自变量不止一个，因变量与自变量的关系要比一元函数复杂得多。在这一节里，我们首先考虑多元函数关于其中一个自变量的变化率。

以二元函数 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 为例，如果只有自变量 𝑥x 变化，而自变量 𝑦y 固定（即看做常量），这时它就是 𝑥x 的一元函数，这函数对 𝑥x 的导数，就称为二元函数 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 对于 𝑥x 的偏导数，即有如下定义：

定义 设函数 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 在点 (𝑥0,𝑦0)(x0​,y0​) 的某一邻域内有定义，当 𝑦y 固定在 𝑦0y0​ 而 𝑥x 在 𝑥0x0​ 处有增量 Δ𝑥Δx 时，相应的函数有增量

如果

存在，那么称此极限为函数 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 在点 (𝑥0,𝑦0)(x0​,y0​) 处对 𝑥x 的偏导数，记作

.

例如，极限可以表为

类似地，函数 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 在点 (𝑥0,𝑦0)(x0​,y0​) 处对 𝑦y 的偏导数定义为

记作

如果函数 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 在区域 𝐷D 内每一点 (𝑥,𝑦)(x,y) 处对 𝑥x 的偏导数都存在，那么这个偏导数就是 𝑥x 和 𝑦y 的函数，它就称为函数 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 对自变量 𝑥x 的偏导函数，记作

类似地，可以定义函数 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 对自变量 𝑦y 的偏导函数，记作

由偏导函数的概念可知，𝑓(𝑥,𝑦)f(x,y) 在点 (𝑥0,𝑦0)(x0​,y0​) 处对 𝑥x 的偏导数 𝑓𝑥(𝑥0,𝑦0)fx​(x0​,y0​) 显然就是偏导函数 𝑓𝑥(𝑥,𝑦)fx​(x,y) 在点 (𝑥0,𝑦0)(x0​,y0​) 处的函数值。

至于实际求 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 的偏导数，并不需要用新的方法，因为这里只有一个自变量在变动，另一个自变量是看做固定的，所以仍旧是一元函数的微分法问题，只要把 𝑦y 暂时看做常量而对 𝑥x 求导数；求对 𝑦y 的偏导数时，只要把 𝑥x 暂时看做常量而对 𝑦y 求导数。

偏导数的概念还可推广到二元以上的函数。例如三元函数 𝑢=𝑓(𝑥,𝑦,𝑧)u=f(x,y,z) 在点 (𝑥,𝑦,𝑧)(x,y,z) 处对 𝑥x 的偏导数定义为

𝑓𝑥(𝑥,𝑦,𝑧)=lim⁡Δ𝑥→0𝑓(𝑥+Δ𝑥,𝑦,𝑧)−𝑓(𝑥,𝑦,𝑧)Δ𝑥,fx​(x,y,z)=limΔx→0​Δxf(x+Δx,y,z)−f(x,y,z)​,

其中 (𝑥,𝑦,𝑧)(x,y,z) 是函数 𝑢=𝑓(𝑥,𝑦,𝑧)u=f(x,y,z) 的定义域的内点。它们的求法也仍旧是一元函数的微分法问题。

例1 求 𝑧=𝑥2+3𝑥𝑦+𝑦2z=x2+3xy+y2 在点 (1,2)(1,2) 处的偏导数。

解：

把 𝑦y 看做常量，得

∂𝑧∂𝑥=2𝑥+3𝑦;∂x∂z​=2x+3y;

把 𝑥x 看做常量，得

∂𝑧∂𝑦=3𝑥+2𝑦.∂y∂z​=3x+2y.

将 (1,2)(1,2) 代入上面的结果，就得

例2 求 𝑧=𝑥2sin⁡2𝑦z=x2sin2y 的偏导数。

解：

例3 设 𝑧=𝑥𝑥(𝑥>0,𝑥≠1)z=xx(x>0,x=1)，求证：

∂𝑧∂𝑥+∂𝑧∂𝑦=𝑧ln⁡𝑥.∂x∂z​+∂y∂z​=zlnx.

证：

因为 𝑧=𝑥𝑥ln⁡𝑥z=xxlnx，所以

所以

例4 求 𝑟=𝑥2+𝑦2+𝑧2r=x2+y2+z2​ 的偏导数。

解：

把 𝑦y 和 𝑧z 都看做常量，得

由于所给函数关于自变量的对称性，所以

例5 已知理想气体的状态方程 𝑝𝑉=𝑅𝑇pV=RT（𝑅R 为常量），求证：

证：

因为

所以

二元函数 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 在点 (𝑥0,𝑦0)(x0​,y0​) 的偏导数有下述几何意义：

设 𝑀0(𝑥0,𝑦0,𝑓(𝑥0,𝑦0))M0​(x0​,y0​,f(x0​,y0​)) 为曲面 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 上的一点，过 𝑀0M0​ 作平面 𝑦=𝑦0y=y0​，截此曲面得一曲线，此曲线在平面 𝑦=𝑦0y=y0​ 上的方程为 𝑧=𝑓(𝑥,𝑦0)z=f(x,y0​)，则偏导数 𝑓𝑥(𝑥0,𝑦0)fx​(x0​,y0​) 就是这曲线在点 𝑀0M0​ 处的切线 𝑀0𝑇M0​T 对 𝑥x 轴的斜率。同样，偏导数 𝑓𝑦(𝑥0,𝑦0)fy​(x0​,y0​) 的几何意义是曲面被平面 𝑥=𝑥0x=x0​ 所截得的曲线在点 𝑀0M0​ 处的切线 𝑀0𝑇M0​T 对 𝑦y 轴的斜率。

我们已经知道，如果一元函数在某点具有导数，那么它在该点必定连续。但对于多元函数来说，即使各偏导数在某点都存在，也不能保证函数在该点连续。这是因为各偏导数存在只能保证点 𝑃P 沿着平行于坐标轴的方向趋于 𝑃0P0​ 时，函数值 𝑓(𝑃)f(P) 趋于 𝑓(𝑃0)f(P0​)，但不能保证点 𝑃P 按任何方式趋于 𝑃0P0​ 时，函数值 𝑓(𝑃)f(P) 都趋于 𝑓(𝑃0)f(P0​)。

例如，函数

在点 (0,0)(0,0) 对 𝑥x 的偏导数为

同样有

但是在第一节中已经知道这函数在点 (0,0)(0,0) 并不连续。

通过以上内容，我们对偏导数的定义、计算方法、几何意义和连续性有了较为全面的了解。在接下来的学习中，我们将进一步探讨偏导数的应用和更高级的微分概念。

设函数 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 在区域 𝐷D 内具有偏导数：

于是，在 𝐷D 内 𝑓𝑥(𝑥,𝑦)fx​(x,y) 和 𝑓𝑦(𝑥,𝑦)fy​(x,y) 都是 𝑥x 和 𝑦y 的函数。如果这两个函数的偏导数也存在，那么称它们是函数 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 的二阶偏导数。按照对变量求导次序的不同，有下列四个二阶偏导数：

其中第二、第三两个偏导数称为混合偏导数。同样可得三阶、四阶……以及 𝑛n 阶偏导数。二阶及二阶以上的偏导数统称为高阶偏导数。

例6 设 𝑧=𝑥3𝑦2−3𝑥𝑦3−𝑥𝑦+1z=x3y2−3xy3−xy+1，求：

𝑓𝑥, 𝑓𝑦, 𝑓𝑥𝑥, 𝑓𝑥𝑦, 𝑓𝑦𝑥, 𝑓𝑦𝑦.fx​,fy​,fxx​,fxy​,fyx​,fyy​.

解：

首先计算一阶偏导数：

然后计算二阶偏导数：

我们看到例6中两个二阶混合偏导数相等，即：

𝑓𝑥𝑦=𝑓𝑦𝑥.fxy​=fyx​.

这不是偶然的，事实上，有下述定理：

定理 如果函数 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 的两个二阶混合偏导数在区域 𝐷D 内连续，那么在该区域内这两个二阶混合偏导数必相等。

换句话说，二阶混合偏导数在连续的条件下与求导的次序无关。这定理的证明从略。

对于二元以上的函数，也可以类似地定义高阶偏导数，而且高阶混合偏导数在偏导数连续的条件下也与求导的次序无关。

例7 验证函数 满足方程：

解：

因为

所以

同理，

因此，

例8 证明函数 𝑢=𝑥2+𝑦2+𝑧2u=x2+y2+z2​ 满足方程：

其中 𝑟=𝑥2+𝑦2+𝑧2r=x2+y2+z2​。

解：

因为

同理，

因此，

例7和例8中的两个方程都叫做拉普拉斯（Laplace）方程，它是数学物理方程中一种很重要的方程。