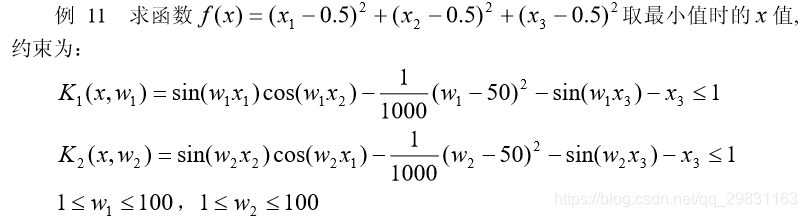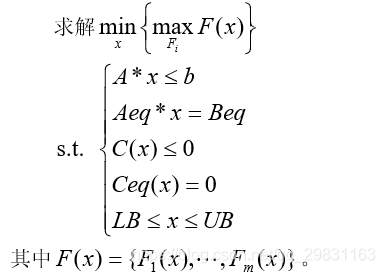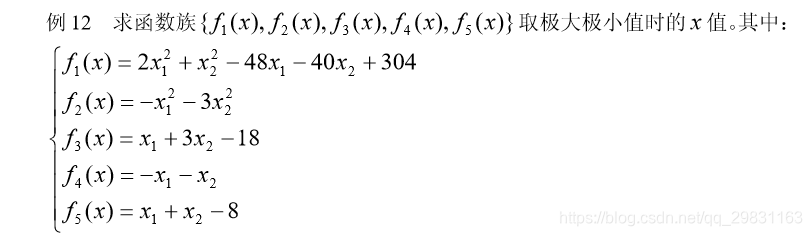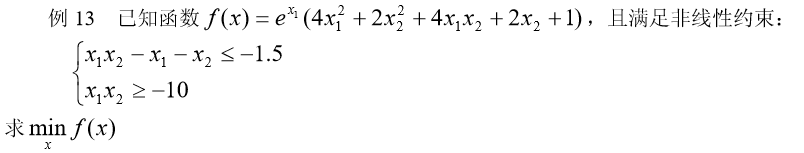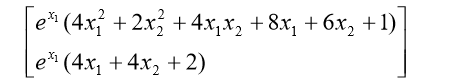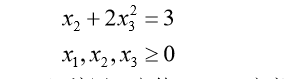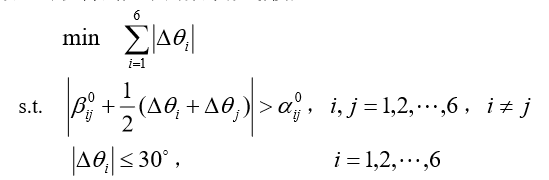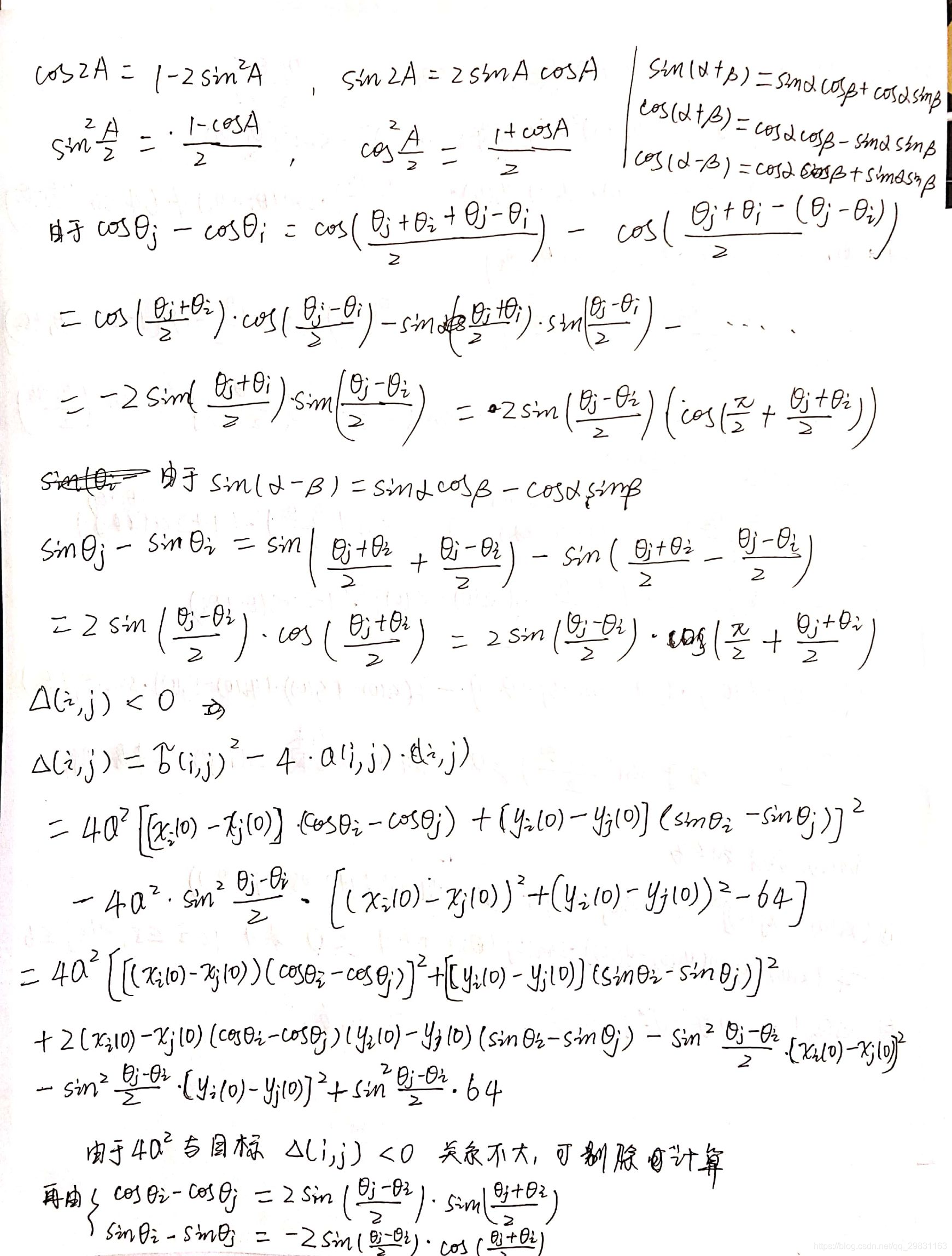非线性规划(二): Matlab 求解约束极值问题 |
您所在的位置:网站首页 › 一元二次函数求最值例题 › 非线性规划(二): Matlab 求解约束极值问题 |
非线性规划(二): Matlab 求解约束极值问题
|
非线性规划(一):定义与数值优化方法(梯度法、牛顿法、拟牛顿法、变尺度法) 非线性规划(二): Matlab 求解约束极值问题 目录 约束极值问题 1 二次规划 2 罚函数法 3 Matlab 求约束极值问题 3.1 fminbnd 函数 3.2 fseminf 函数 3.3 fminimax 函数 4 Matlab 优化工具箱的用户图形界面解法 4 非线性规划的应用:飞行管理问题 4.1 模型一 4.2 模型二 习 题 约束极值问题带有约束条件的极值问题称为约束极值问题,也叫规划问题。 求解约束极值问题要比求解无约束极值问题困难得多。为了简化其优化工作,可采用以下方法:将约束问题化为无约束问题;将非线性规划问题化为线性规划问题,以及 能将复杂问题变换为较简单问题的其它方法。 库恩—塔克条件是非线性规划领域中重要的理论成果之一,是确定某点为优点 的必要条件,但一般说它并不是充分条件(对于凸规划,它既是优点存在的必要条件, 同时也是充分条件)。 无约束问题的求解请参考这里:非线性规划(一):定义与数值优化方法 1 二次规划若某非线性规划的目标函数为自变量 x的二次函数,约束条件又全是线性的,就称 这种规划为二次规划。
Matlab 中求解二次规划的命令是 [X,FVAL]= QUADPROG(H,f,A,b,Aeq,beq,LB,UB,X0,OPTIONS)返回值 X 是决策向量 x的值,返回值 FVAL 是目标函数在 x处的值。(具体细节可以参 看在 Matlab 指令中运行 help quadprog 后的帮助)。
利用罚函数法,可将非线性规划问题的求解,转化为求解一系列无约束极值问题, 因而也称这种方法为序列无约束小化技术,简记为 SUMT (Sequential Unconstrained Minization Technique)。 罚函数法求解非线性规划问题的思想是,利用问题中的约束函数作出适当的罚函 数,由此构造出带参数的增广目标函数,把问题转化为无约束非线性规划问题。主要有 两种形式,一种叫外罚函数法,另一种叫内罚函数法,下面介绍外罚函数法。
解 (i)编写 M 文件 test.m function g=test(x); M=50000; f=x(1)^2+x(2)^2+8; g=f-M*min(x(1),0)-M*min(x(2),0)-M*min(x(1)^2-x(2),0)+... M*abs(-x(1)-x(2)^2+2);或者是利用Matlab的求矩阵的极小值和极大值函数编写test.m如下: function g=test(x); M=50000; f=x(1)^2+x(2)^2+8; g=f-M*sum(min([x';zeros(1,2)]))-M*min(x(1)^2-x(2),0)+... M*abs(-x(1)-x(2)^2+2);我们也可以修改罚函数的定义,编写test.m如下: function g=test(x); M=50000; f=x(1)^2+x(2)^2+8; g=f-M*min(min(x),0)-M*min(x(1)^2-x(2),0)+M*(-x(1)-x(2)^2+2)^2;(ii)在 Matlab 命令窗口输入 [x,y]=fminunc('test',rand(2,1))即可求得问题的解。 3 Matlab 求约束极值问题在 Matlab 优化工具箱中,用于求解约束优化问题的函数有:fminbnd、fmincon、 quadprog、fseminf、fminimax,上面我们已经介绍了函数 fmincon 和 quadprog。 3.1 fminbnd 函数求单变量非线性函数在区间上的极小值
Matlab 的命令为 [X,FVAL] = FMINBND(FUN,x1,x2,OPTIONS)它的返回值是极小点x 和函数的极小值。这里 fun 是用 M 文件定义的函数或 Matlab 中 的单变量数学函数。
上述问题的 Matlab 命令格式为 X=FSEMINF(FUN,X0,NTHETA,SEMINFCON,A,B,Aeq,Beq)
解 (1)编写 M 文件 fun6.m 定义目标函数如下: function f=fun6(x,s); f=sum((x-0.5).^2);(2)编写 M 文件 fun7.m 定义约束条件如下: function [c,ceq,k1,k2,s]=fun7(x,s); c=[];ceq=[]; if isnan(s(1,1)) s=[0.2,0;0.2 0]; end %取样值 w1=1:s(1,1):100; w2=1:s(2,1):100; %半无穷约束 k1=sin(w1*x(1)).*cos(w1*x(2))-1/1000*(w1-50).^2-sin(w1*x(3))-x(3)-1; k2=sin(w2*x(2)).*cos(w2*x(1))-1/1000*(w2-50).^2-sin(w2*x(3))-x(3)-1; %画出半无穷约束的图形 plot(w1,k1,'-',w2,k2,'+');(3)调用函数 fseminf 在 Matlab 的命令窗口输入 [x,y]=fseminf(@fun6,rand(3,1),2,@fun7)即可求得结果。 3.3 fminimax 函数
上述问题的 Matlab 命令为 X=FMINIMAX(FUN,X0,A,B,Aeq,Beq,LB,UB,NONLCON)
解 (1)编写 M 文件 fun8.m 定义向量函数如下: function f=fun8(x); f=[2*x(1)^2+x(2)^2-48*x(1)-40*x(2)+304 -x(1)^2-3*x(2)^2 x(1)+3*x(2)-18 -x(1)-x(2) x(1)+x(2)-8];(2)调用函数 fminimax [x,y]=fminimax(@fun8,rand(2,1))3.3.4 利用梯度求解约束优化问题
分析:当使用梯度求解上述问题时,效率更高并且结果更准确。 题目中目标函数的梯度为:
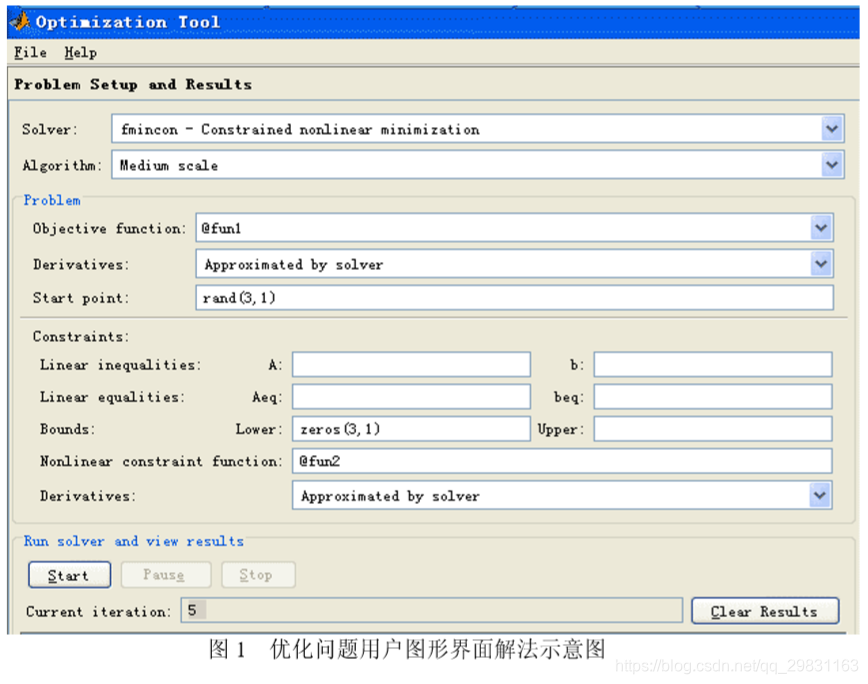
解 (1)编写 M 文件 fun9.m 定义目标函数及梯度函数: function [f,df]=fun9(x); f=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1); df=[exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+8*x(1)+6*x(2)+1);exp(x(1))*(4*x(2) +4*x(1)+2)];(2)编写 M 文件 fun10.m 定义约束条件及约束条件的梯度函数: function [c,ceq,dc,dceq]=fun10(x); c=[x(1)*x(2)-x(1)-x(2)+1.5;-x(1)*x(2)-10]; dc=[x(2)-1,-x(2);x(1)-1,-x(1)]; ceq=[];dceq=[];(3)调用函数 fmincon,编写主函数文件 example13.m 如下: %采用标准算法 options=optimset('largescale','off'); %采用梯度 options=optimset(options,'GradObj','on','GradConstr','on'); [x,y]=fmincon(@fun9,rand(2,1),[],[],[],[],[],[],@fun10,options) 4 Matlab 优化工具箱的用户图形界面解法Matlab 优化工具箱中的 optimtool 命令提供了优化问题的用户图形界面解法。 optimtool 可应用到所有优化问题的求解,计算结果可以输出到 Matlab 工作空间中。
例 14 用 optimtool 重新求解例 2。
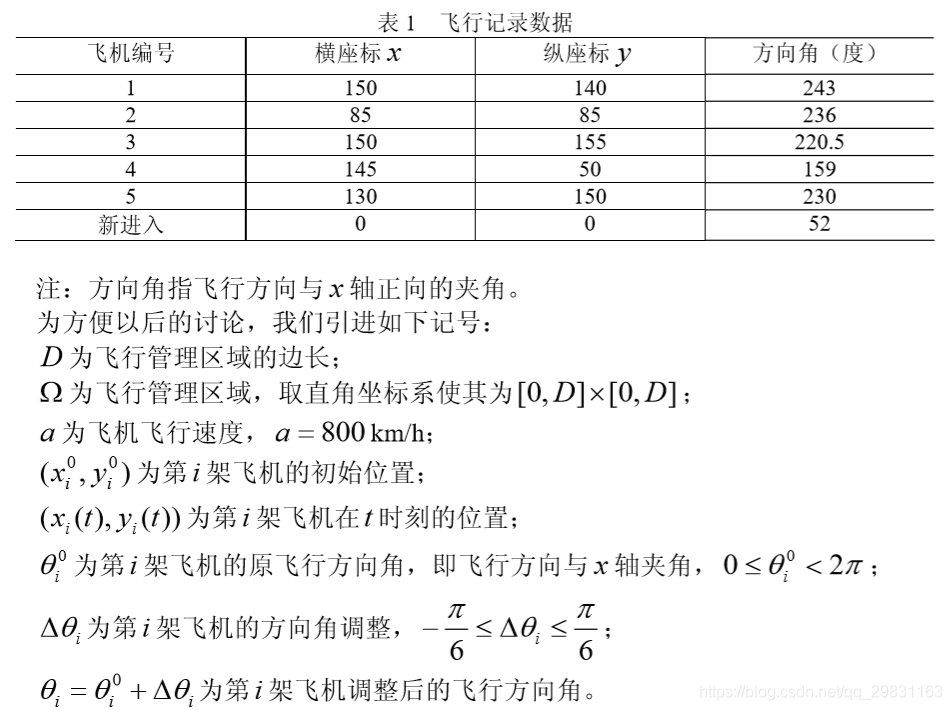
解 (i)编写 M 文件 fun1.m 定义目标函数 function f=fun1(x); f=sum(x.^2)+8;(ii)编写M文件fun2.m定义非线性约束条件 function [g,h]=fun2(x); g=[-x(1)^2+x(2)-x(3)^2 x(1)+x(2)^2+x(3)^3-20]; %非线性不等式约束 h=[-x(1)-x(2)^2+2 x(2)+2*x(3)^2-3]; %非线性等式约束利用例 2 已经定义好的函数 fun1 和 fun2。在 Matlab 命令窗口运行 optimtool,就打 开图形界面,如图 1 所示,填入有关的参数,未填入的参数取值为空或者为默认值,然 后用鼠标点一下“start”按钮,就得到求解结果,再使用“file”菜单下的“Export to Workspace…”选项,把计算结果输出到 Matlab 工作空间中去。 4 非线性规划的应用:飞行管理问题 在约 10,000m 高空的某边长 160km 的正方形区域内,经常有若干架飞机作水平 飞行。区域内每架飞机的位置和速度向量均由计算机记录其数据,以便进行飞行管理。 当一架欲进入该区域的飞机到达区域边缘时,记录其数据后,要立即计算并判断是否会 与区域内的飞机发生碰撞。如果会碰撞,则应计算如何调整各架(包括新进入的)飞机 飞行的方向角,以避免碰撞。现假定条件如下: 1)不碰撞的标准为任意两架飞机的距离大于 8km; 2)飞机飞行方向角调整的幅度不应超过 30 度; 3)所有飞机飞行速度均为每小时 800km; 4)进入该区域的飞机在到达区域边缘时,与区域内飞机的距离应在 60km 以上; 5)多需考虑 6 架飞机; 6)不必考虑飞机离开此区域后的状况。 请你对这个避免碰撞的飞行管理问题建立数学模型,列出计算步骤,对以下数据进 行计算(方向角误差不超过 0.01 度),要求飞机飞行方向角调整的幅度尽量小。 设该区域 4 个顶点的座标为(0,0),(160,0),(160,160),(0,160)。记录数据见表 1。
本问题中的优化目标函数可以有不同的形式:如使所有飞机的大调整量小; 所有飞机的调整量绝对值之和小等。这里以所有飞机的调整量绝对值之和小为目标 函数,可以得到如下的数学规划模型:
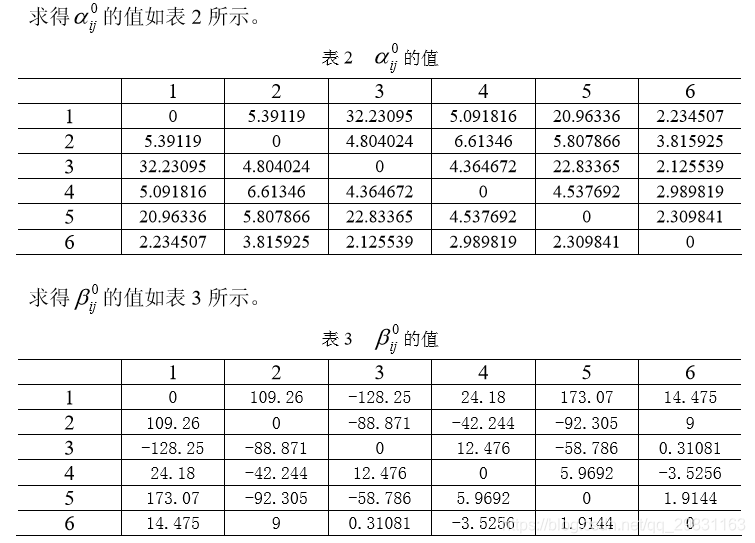
利用如下的程序: clc,clear x0=[150 85 150 145 130 0]; y0=[140 85 155 50 150 0]; q=[243 236 220.5 159 230 52]; xy0=[x0; y0]; d0=dist(xy0); %求矩阵各个列向量之间的距离 d0(find(d0==0))=inf; a0=asind(8./d0) %以度为单位的反函数 xy1=x0+i*y0 xy2=exp(i*q*pi/180) for m=1:6 for n=1:6 if n~=m b0(m,n)=angle((xy2(n)-xy2(m))/(xy1(m)-xy1(n))); end end end b0=b0*180/pi; dlmwrite('txt1.txt',a0,'delimiter', '\t','newline','PC'); fid=fopen('txt1.txt','a'); fwrite(fid,'~','char'); %往纯文本文件中写 LINGO 数据的分割符 dlmwrite('txt1.txt',b0,'delimiter', '\t','newline','PC','-append','roffset', 1)
上述飞行管理的数学规划模型可如下输入 LINGO 求解: model: sets: plane/1..6/:delta; link(plane,plane):alpha,beta; endsets data: alpha=@file('txt1.txt'); !需要在alpha的数据后面加上分隔符"~"; beta=@file('txt1.txt'); enddata min=@sum(plane:@abs(delta)); @for(plane:@bnd(-30,delta,30)); @for(link(i,j)|i#ne#j:@abs(beta(i,j)+0.5*delta(i)+0.5*delta(j))>a lpha(i,j)); end
4.2 模型二
计算到这里也没有展开的必要了。由于目标的约束是< 0和 |
【本文地址】
今日新闻 |
推荐新闻 |