傅里叶变换、拉普拉斯变换、Z 变换的联系是什么?为什么要进行这些变换? |
您所在的位置:网站首页 › z变换的目的 › 傅里叶变换、拉普拉斯变换、Z 变换的联系是什么?为什么要进行这些变换? |
傅里叶变换、拉普拉斯变换、Z 变换的联系是什么?为什么要进行这些变换?
|
原创 逸珺 嵌入式客栈 [导读] 在知乎上看到一个问题,傅里叶变换、拉普拉斯变换、Z 变换的联系是什么?为什么要进行这些变换?我觉得这是一个非常好的问题,貌似一下子也回答不上来,所以整理学习并分享一下。
要理解这些变换,首先需要理解什么是数学变换!如果不理解什么是数学变换的概念,那么其他的概念我觉得也没有理解。 数学变换是指数学函数从原向量空间在自身函数空间变换,或映射到另一个函数空间,或对于集合X到其自身(比如线性变换)或从X到另一个集合Y的可逆变换函数。比如(图片来源wikipedia):
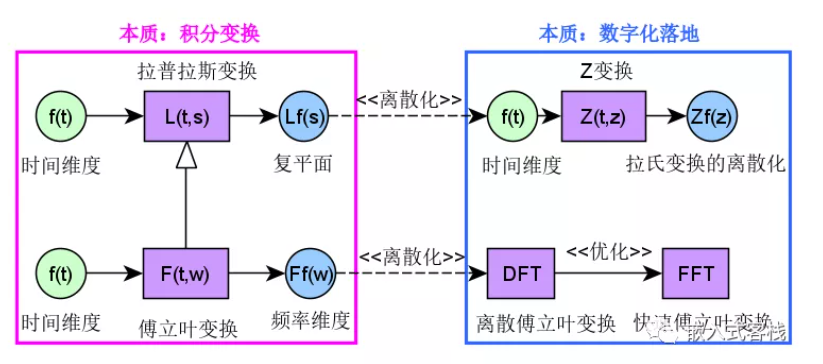
数学中还有很多其他的数学变换,其本质都可以看成是将函数f(x)利用变换因子进行的一种数学映射,其变换结果是函数的自变量有可能还是原来的几何向量空间,或许会变成其他的几何向量空间,比如傅立叶变换就从时域变换为频域。 而傅立叶变换和拉普拉斯变换的本质都是对连续或有限个第一类间断点函数的一种积分变换,那么什么是积分变换呢? 什么是积分变换?积分变换通过对原函数对映射函数空间自变量在特定区间进行积分运算,将函数从其原始函数空间映射到另一个函数空间。这样一来,其中原始函数的某些属性在映射函数空间可能比原始函数空间更容易表征或分析。通常可以使用逆变换将变换后的函数映射回到原函数空间,这样的变换称为可逆变换。 假定对于函数为自变量t的函数f(t),通常积分变换都具有如下类似的范式:
(
T
f
)
(
u
)
=
∫
t
1
t
2
f
(
t
)
K
(
t
,
u
)
d
t
(Tf)(u)=\int_{t1}^{t2}{f(t)K(t,u)dt}
(Tf)(u)=∫t1t2f(t)K(t,u)dt 函数f(t)是该变换的输入,(Tf)(u)为变换的输出,因此积分变换一般也称为一种特定的数学运算符。而函数K(t,u)称为积分核函数(kernel function)。 有的变换可逆,这是什么概念呢?就是变换后通过逆变换,还能还原! f ( t ) = ∫ u 1 u 2 ( T f ) ( u ) K − 1 ( u , t ) d u f(t)=\int_{u_1}^{u_2}{(Tf)(u)K^{-1}(u,t)du} f(t)=∫u1u2(Tf)(u)K−1(u,t)du 观察正变换与逆变换,你会发现: 核函数刚好两个自变量交换位置正变换是对原函数f(t)在时间维度上进行积分逆变换是在变换后的函数在u维度上进行积分 什么是傅立叶级数?在谈傅立叶变换之前,先谈谈傅立叶级数会更容易理解傅立叶变换。在数学中,傅里叶级数(Fourier series)是把类似波的函数表示成简单正弦波的方式。更正式的说法是,它能将任何周期性函数或周期性信号分解成一个(可能由无穷个频率分量组成的)简单振荡函数的集合,即正弦函数和余弦函数(或者,等价地使用复指数),从数学的定义来看: 设f(t)是一周期信号,假定其周期为T。若f(t)在一个周期的能量是有限的,就是: ∫ − T 2 T 2 ∣ f ( t ) ∣ d t < ∞ \int_{-\frac{T}{2}}^{\frac{T}{2}}|f(t)|dt\lt\infty ∫−2T2T∣f(t)∣dt σ 0 ) \lim_{x->\infty}{f(t)e^{-\sigma t}}=0(\sigma \gt \sigma_0) x−>∞limf(t)e−σt=0(σ>σ0) 傅立叶拉氏变换联系区别所以傅立叶变换与拉普拉斯变换的联系就比较容易联系了。 Z变换本质上是拉普拉斯变换的离散形式。也称为Fisher-Z变换。对于连续信号进行抽样变换就得到了原函数的离散序列:
f
s
(
t
)
=
f
(
t
)
⋅
δ
T
(
t
)
=
∑
n
=
0
∞
f
(
n
T
)
δ
(
t
−
n
T
)
f_s(t)=f(t)\cdot \delta_T(t)=\sum_{n=0}^{\infty}f(nT)\delta(t-nT)
fs(t)=f(t)⋅δT(t)=n=0∑∞f(nT)δ(t−nT) 其中T为采样周期,
δ
T
(
t
)
\delta_T(t)
δT(t)信号与系统中称为冲激抽样。其实说人话,就是将连续信号,按等间隔理想的转为抽取离散序列样本。看下图就明白了,在电子系统中常用AD转换器进行实现。 这就是Z变换了,从上面的过程描述就知道Z变换与拉普拉斯变换的关系了。因此两者的联系也就是Z变换是拉布拉斯变换的离散形式。
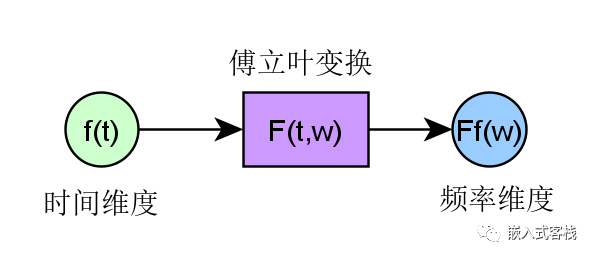
这里谈到Z变换的离散形式,那么这里也提一句,傅立叶变换数字落地,也即离散形式是离散傅立叶变换DFT(Discrete Fourier Transform),而大家所熟知的快速傅立叶变换FFT(Fast Fourier Transform)则是DFT的高效率实现。 总结一下要理解三种变换的联系区别,首先要理解什么是数学变换,什么是积分变换。傅立叶变换以及拉普拉斯变换本质上都是连续或有限个第一类间断点函数的积分变换,而傅立叶变换是拉普拉斯变换的特殊形式,而Z变换是拉普拉斯变换的离散形式。每种变换都有其应用价值,傅立叶变换在信号处理的频域分析中提供了强大的数学工具,而拉普拉斯变换在电子学、控制工程、航空航天等领域提供了建模、分析的数学分析工具;Z变换则将这些变换进而落地为数字实现提供数学理论依据。DFT为FFT的离散化形式,而FFT是DFT的算法优化实现。 |
【本文地址】
今日新闻 |
推荐新闻 |

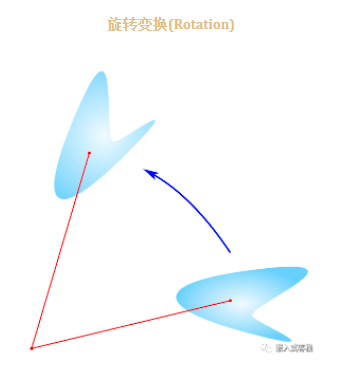
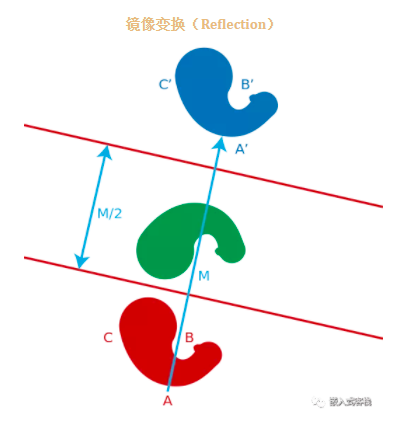

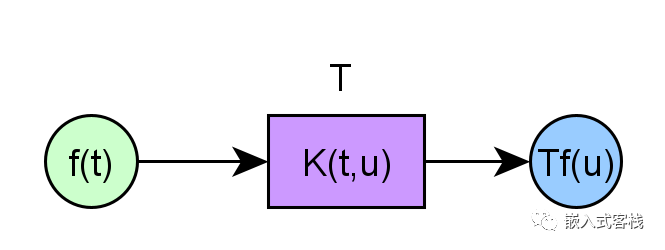 这里有一个对称核函数的概念,这是什么意思呢?就是将函数K的两个自变量交换位置仍然相等:
K
(
t
,
u
)
=
K
(
u
,
t
)
K(t,u)=K(u,t)
K(t,u)=K(u,t)
这里有一个对称核函数的概念,这是什么意思呢?就是将函数K的两个自变量交换位置仍然相等:
K
(
t
,
u
)
=
K
(
u
,
t
)
K(t,u)=K(u,t)
K(t,u)=K(u,t)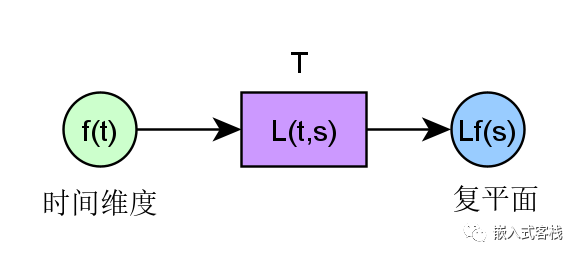
 对上式进行拉普拉斯变换:
F
s
(
S
)
=
∫
0
∞
[
∑
n
=
0
∞
f
(
n
T
)
δ
(
t
−
n
T
)
]
e
−
s
t
d
t
F_s(S)=\int_0^\infty[\sum_{n=0}^{\infty}f(nT)\delta(t-nT)]e^{-st}dt
Fs(S)=∫0∞[n=0∑∞f(nT)δ(t−nT)]e−stdt 该公式利用冲激函数的抽样特性,可简化为:
F
s
(
S
)
=
∑
n
=
0
∞
f
(
n
T
)
e
−
s
n
T
F_s(S)=\sum_{n=0}^{\infty}f(nT)e^{-snT}
Fs(S)=n=0∑∞f(nT)e−snT 引入
z
=
e
s
T
z=e^{sT}
z=esT,引入新的自变量Z,则上面的公式就变成这样了:
F
(
Z
)
=
∑
n
=
0
∞
f
(
n
T
)
Z
−
n
F(Z)=\sum_{n=0}^{\infty}f(nT)Z^{-n}
F(Z)=n=0∑∞f(nT)Z−n
对上式进行拉普拉斯变换:
F
s
(
S
)
=
∫
0
∞
[
∑
n
=
0
∞
f
(
n
T
)
δ
(
t
−
n
T
)
]
e
−
s
t
d
t
F_s(S)=\int_0^\infty[\sum_{n=0}^{\infty}f(nT)\delta(t-nT)]e^{-st}dt
Fs(S)=∫0∞[n=0∑∞f(nT)δ(t−nT)]e−stdt 该公式利用冲激函数的抽样特性,可简化为:
F
s
(
S
)
=
∑
n
=
0
∞
f
(
n
T
)
e
−
s
n
T
F_s(S)=\sum_{n=0}^{\infty}f(nT)e^{-snT}
Fs(S)=n=0∑∞f(nT)e−snT 引入
z
=
e
s
T
z=e^{sT}
z=esT,引入新的自变量Z,则上面的公式就变成这样了:
F
(
Z
)
=
∑
n
=
0
∞
f
(
n
T
)
Z
−
n
F(Z)=\sum_{n=0}^{\infty}f(nT)Z^{-n}
F(Z)=n=0∑∞f(nT)Z−n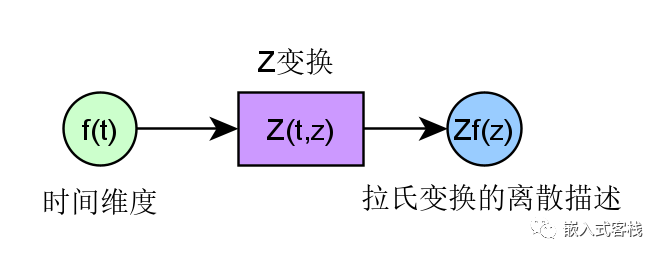 那么Z变换的意义在于什么呢?在数字信号处理以及数字控制系统中,Z变换提供了数学基础。利用Z变换很快就能将一个传递函数描述成差分方程形式,这就为编程实现提供了数学依据,比如一个数字滤波器知道其Z变换形式,写代码就是分分钟的事情了,同样知道一个控制算法的Z变换形式,同样编代码也是水到渠成的事情。
那么Z变换的意义在于什么呢?在数字信号处理以及数字控制系统中,Z变换提供了数学基础。利用Z变换很快就能将一个传递函数描述成差分方程形式,这就为编程实现提供了数学依据,比如一个数字滤波器知道其Z变换形式,写代码就是分分钟的事情了,同样知道一个控制算法的Z变换形式,同样编代码也是水到渠成的事情。