高等数学II

您所在的位置：网站首页 › ye-y的原函数 › 高等数学II

高等数学II

2024-07-08 19:01| 来源: 网络整理| 查看: 265

原函数的概念

不定积分

定义

不定积分的基本积分公式

不定积分的运算法则

求原函数的两种常用方法

第一换元法（凑微分法）

第二换元法

分部积分法

有理函数原函数求法

典型三角函数原函数求法

原函数的概念

设 $f(x)$ 在区间 $I$ 上有定义，若存在函数 $F(x)$ ,对任意 $x\in I$ ，都有 $F'(x)=f(x)$ 或 $dF(x)=f(x)dx$ .

则称 $F(x)$ 为 $f(x)$ 在区间 $I$ 上的一个原函数。

例：由 $(\frac{x^3}{3})'=x^2$ ，知 $\frac{x^3}{3}$ 是 $x^2$ 在 $\left (- \infty,+\infty \right )$ 上的一个原函数；

由 $(sinx)'=cosx$ ，知 $sinx$ 是 $cosx$ 在 $\left (- \infty,+\infty \right )$ 上的一个原函数。

因为： $(sinx+1)'=cosx,(sinx+10)'=cosx......$ （原函数可以有无数个）

所以：原函数可以表达为 $sinx+C$

不定积分

定义

函数 $f(x)$ 的全体函数 $F(x)+C$ 称为 $f(x)$ 的不定积分，记作 $\int f(x)dx$ ，即

$\int f(x)dx=F(x)+C$

其中，“ $\int$ ”表示积分号， $f(x)$ 为被积函数， $f(x)dx$ 为被积表达式， $x$ 为积分变量， $C$ 为积分常数。

不定积分的基本积分公式

不定积分的运算法则

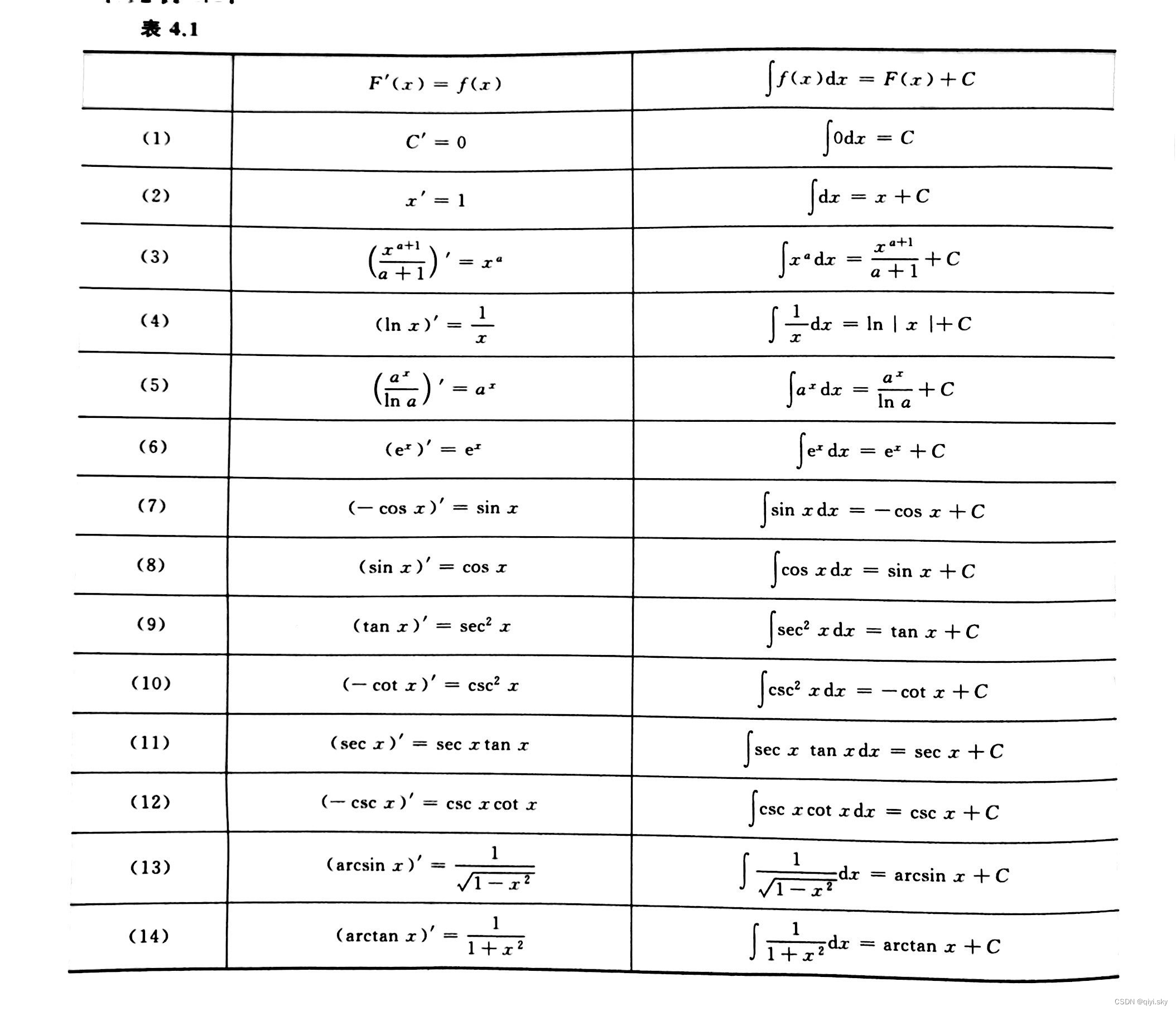
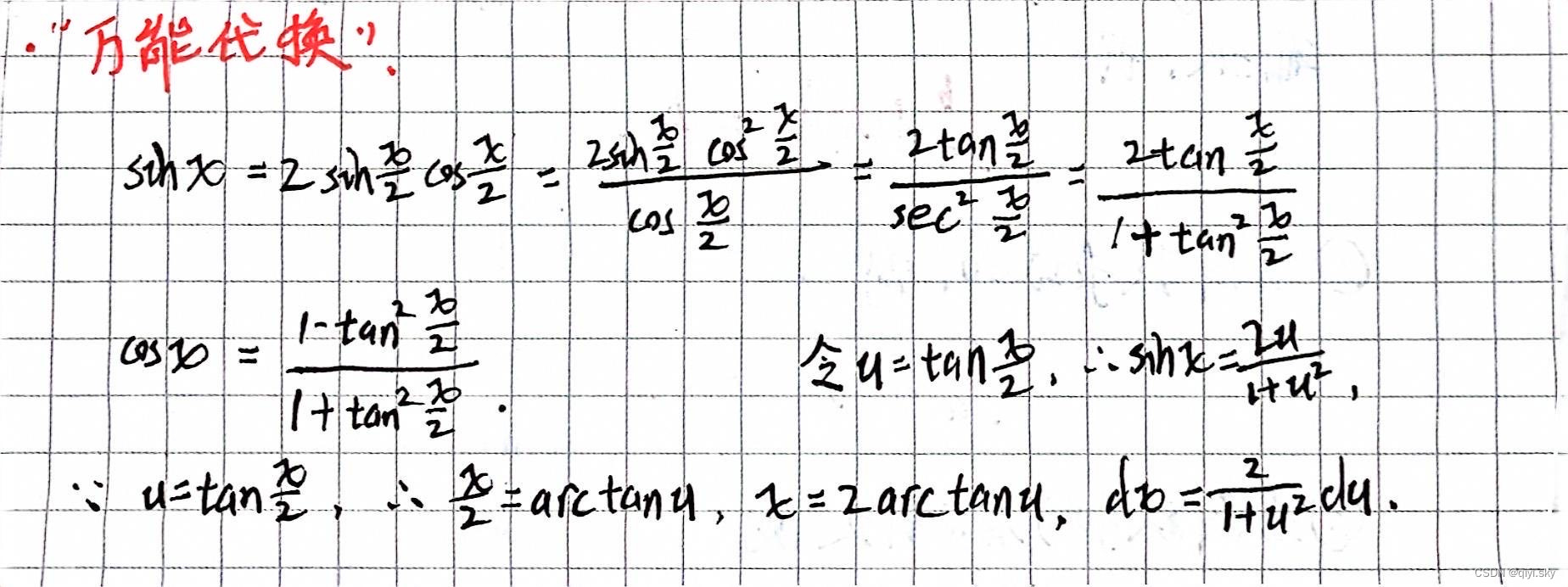
（1）被积函数中不为0的常数因子可以提出来：

$\int kf(x)dx=k\int f(x)dx\: \: (k\neq 0)$

（2）两个函数代数和的不定积分等于这两个函数不定积分的代数和

$\int [f_1(x)\pm f_2(x)]dx=\int f_1(x)dx\pm \int f_2(x)dx$

求原函数的两种常用方法

第一换元法（凑微分法）

例： $\int sin^2x\, cosxdx$

一、找到复合函数

$(sinx)^2$

二、由 $d(sinx)=sin'x\cdot dx=cosx\cdot dx$

$\int (sinx)^2\cdot d(sinx)$

三、换元，令u=sinx

$\int u^2du$

四、求出来后回代

$\int u^2du=\frac{1}{3}u^3+C=\frac{1}{3}(sinx)^3+C$

要熟练应用第一换元法，需要有效地凑出：

$f[\varphi (x)]\varphi '(x)dx=f(u)du$

第二换元法

例： $\int \frac{1}{1+\sqrt{x}}dx$

令 $\sqrt{x}=t$ ，则 $x=t^2,dx=2tdt$ 。

$\begin{matrix} \therefore \int \frac{1}{1+\sqrt{x}}dx &= &\int \frac{1}{1+t}2tdt\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \\ &= &2\int \frac{t}{1+t}dt\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \\ &= &2t+2\ln \left | 1+t \right |+C\: \: \: \: \: \: \: \:\: \\ &= &2\sqrt{x} -2 \ln\left | 1+\sqrt{x} \right |+C \end{matrix}$

第二换元法积分公式： $\int f(x)dx=G[\varphi^{-1}(x) ]+C$

第二换元法的三角换元法

$\begin{matrix} \textbf{a}.sin^2t+cos^2t=1\\ \textbf{b}.1+tan^2t=sec^2t\\ \textbf{c}.1+cot^2t=csc^2t \end{matrix}$

当被积函数中含 $\sqrt{a^2-x^2}$ 时，设 $x=asint\: \: \: (-\frac{\pi}{2}t\frac{\pi}{2})$

当被积函数中含 $\sqrt{a^2+x^2}$ 时，设 $x=atant\: \: \: (-\frac{\pi}{2}t\frac{\pi}{2})$

当被积函数中含 $\sqrt{x^2-a^2}$ 时，设 $x=asect\: \: \: (0t\frac{\pi}{2})$

分部积分法

$(uv)'=u'v+uv'$ 两边同时积分

$\int (uv)'dx=\int u'vdx+\int uv'dx$

$uv=\int vdu+\int udv$

于是，得到分部积分公式： $\int udv=uv-\int vdu$

例： $\int x\cdot sinxdx$

$\int x\cdot sinxdx=\int x\cdot d(-cosx)=-xcosx-\int -cosxdx=-xcosx+sinx+C$

特殊题型 $\int e^xsinxdx$

$\begin{matrix} & &\int e^xsinxdx\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \\ &= &-e^xcosx-\int -cosxd(e^x) \: \: \: \: \: \: \: \: \: \: \: \: \: \: \\ &= &-e^xcosx+e^xsinx-\int sinxd(e^x) \\ &= &-e^xcosx+e^xsinx-\int e^xsinxdx \end{matrix}$

移到等式左边

$2\int e^xsinxdx=-e^xcos+e^xsinx$

需要对左式再进行分部积分。

有理函数原函数求法

典型三角函数原函数求法

end

【本文地址】

高等数学II

高等数学II

今日新闻

推荐新闻