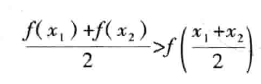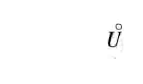人工智能数学基础:利用导数判断函数单调性、凹凸性、极值、最值和描绘函数图形 |
您所在的位置:网站首页 › xe的x2求二阶导 › 人工智能数学基础:利用导数判断函数单调性、凹凸性、极值、最值和描绘函数图形 |
人工智能数学基础:利用导数判断函数单调性、凹凸性、极值、最值和描绘函数图形
 一、单调性判断定理
一、单调性判断定理
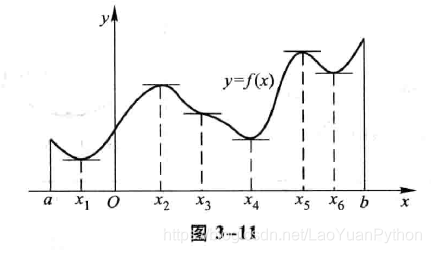
定理: 设函数y=f(x)在[a,b]上连续,在(a,b)内可导。 (1)如果在(a,b)内f(x)≥0,且等号仅在有限多个点处成立,那么函数y=f(x)在[a,b]上单调增加; (2)如果在(a,b)内f(x)≤0,且等号仅在有限多个点处成立,那么函数y=f(x)在[a,b]上单调减少。 证明思路: 利用拉格朗日中值公式,可以正得任意两点的函数值差等于某点导数与两点x值的差的乘积,因此x值的差决定了函数值的差的符号。 另外对于导数为0的点,将区间分成了2部分,每部分的单调性跟随导数的值与自变量的差的值,这表明两个区间的单调性遵循定理的要求,则两个区间叠加后也会遵循。 二、曲线凹凸性判断 1、凹凸性的判断规则函数曲线的上升或下降反映了函数的单调性,而曲线在上升或下降过程中,还存在一个弯曲方向的问题,如图: 都是上升曲线,曲线ACB向上凸起,而ADB则向下弯曲。 曲线的凹凸性在几何图形上的描述:通过曲线上任取两点,如果连接这两点的直线(弦)总是位于这两点曲线弧的上方,则曲线是向下弯曲(凹),如果弦总是位于曲线弧的上方,则曲线是向上凸的。 曲线的凹凸性函数形式的表达: 设f(x)在区间I上连续,如果对I上任意两点x1、x2恒有: 设f(x)在[a,b]上连续,在(a,b)内具有一阶和二阶导数,那么 (1)若在(a,b)内f”(x)>0,则f(x)在[a,b]上的图形是凹的; (2)若在(a,b)内f”(x)x1,然后取x0=(x1+x2)/2,记h=x0-x1=x2-x0,分别对区间[x1,x0]、[x0,x2]应用柯西中值定理,得到的两个式子相减后再应用柯西中值定理,如果函数f(x)的二阶导数大于0,就可以得到: 设函数f(x)在点x0的某邻域U(x0)内有定义,如果对于去心邻域U°(x0)内的任一x,有 f(x)f(x0)),那么就称f(x0)是函数f(x)的一个极大值(或极小值)。 备注:去心邻域实际的表示不是U°,而是在U上面一个小圈,但无法用文字输入,因此老猿所有的博文都用了U°来表示,实际的符号应该是: 函数的极大值与极小值统称为函数的极值,使函数取得极值的点称为极值点。 函数的极大值和极小值概念是局部性的。如果f(x0)是函数f(x)的一个极大值,那是就x0附近的一个局部范围来说,f(x0)是f(x)的一个最大值,如果就f(x)的整个定义域来说f(x0)不见得是最大值。关于极小值也类似。
在图3-11中,函数f(x)有两个极大值:f(x2)、f(x5),三个极小值:f(x1)、f(x4)、f(x6),其中极大值f(x2)比极小值f(x0)还小。就整个区间[a,b]来说,只有一个极小值f(x1)同时也是最小值,而没有一个极大值是最大值。 2、定理1(必要条件)定理:设函数f(x)在x0处可导,且在x0处取得极值,则f’(x0)=0。 定理1就是说:可导函数f(x)的极值点必定是它的驻点,但反过来,函数的驻点却不一定是极值点。 例如,f(x)=x3的导数f’(x)=3x2,f’(0)=0,因此x=0是这可导函数的驻点,但x=0却不是这函数的极值点。 所以,函数的驻点只是可能的极值点。此外,函数在它的导数不存在的点处也可能取得极值。 3、定理2(第一充分条件)定理:设函数f(x)在x0处连续,且在x0的某去心邻域U°(x0,δ)内可导。 (1)若x∈(x0-δ,x0)时,f’(x)>0,而x∈(x0,x0+δ)时,f’(x) |
【本文地址】
今日新闻 |
推荐新闻 |
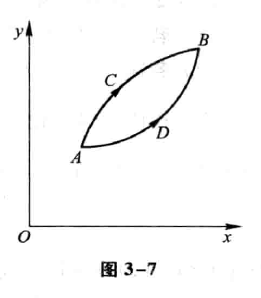
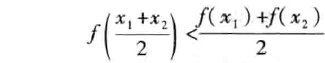 那么称f(x)在I上的图形是(向上)凹的(或凹弧),如果恒有:
那么称f(x)在I上的图形是(向上)凹的(或凹弧),如果恒有: 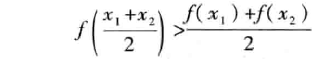 那么称/(x)在I上的图形是(向上)凸的(或凸弧)。
那么称/(x)在I上的图形是(向上)凸的(或凸弧)。