在很久以前整理过支持向量机（SVM）的相关内容，参考 [ML] 支持向量机及对偶问题的推导。SVM 一般用于分类任务，本次我们所提到的支持向量回归（SVR）则是 SVM 在回归分析中的变体。

在 SVM 中我们的目标是通过最大化间隔，找到一个分离超平面（Hyperplane），使得绝大多数的样本点位于两个决策边界（Decision boundary）的外侧。SVR 同样是考虑最大化间隔，但是考虑的是决策边界内的点，使尽可能多的样本点位于间隔内。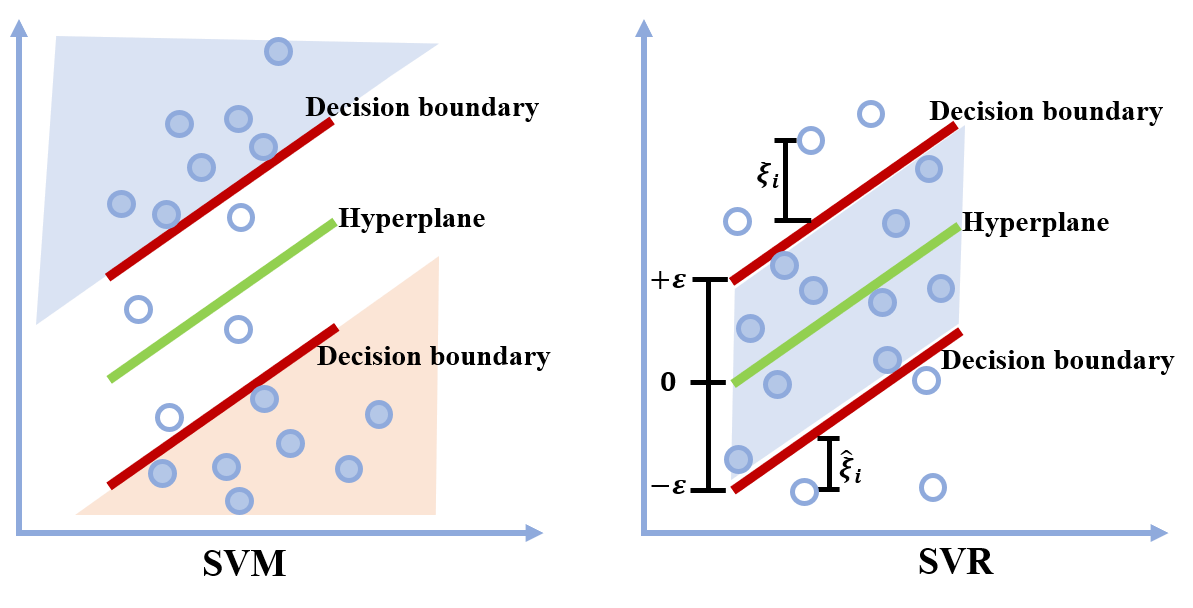

下面直接给出 SVR 的优化问题：

\begin{split} \min_{\boldsymbol{w}} & \; \frac{1}{2} \left\| \boldsymbol{w}\right \|^2\\ \text{s.t. } & \; y_i-\boldsymbol{w}^T\boldsymbol{x}_i -b \leq \varepsilon \\ & \;\boldsymbol{w}^T\boldsymbol{x}_i +b-y_i \leq \varepsilon \end{split}\\

为每个样本点引入松弛变量 \xi_i 或 \hat{\xi}_i ：

\begin{split} \min_{\boldsymbol{w}} & \; \frac{1}{2} \left\| \boldsymbol{w}\right \|^2 + C\sum^{N}_{i=1}\left (\xi_i+\hat{\xi}_i\right )\\ \text{s.t. } & \; y_i-\boldsymbol{w}^T\boldsymbol{x}_i -b \leq \varepsilon + \xi_i\\ & \;\boldsymbol{w}^T\boldsymbol{x}_i +b-y_i \leq \varepsilon +\hat{\xi}_i\\ & \; \xi, \hat{\xi}_i \geq 0 \end{split}\\

从上面的优化问题我们可以看出，SVR 只对间隔（ \varepsilon -insensitive tube）外的样本进行惩罚 ，当样本点位于间隔内时，则不计算其损失。（见第一张图片）

二次规划算法可以用于求解上述优化问题，对于 SVM 问题，SMO 算法一般是最常用的算法。不再赘述，我们先写出它的对偶问题。。

Lagrange 函数为：（符号上这里尽量与《机器学习》中保持一致）

\begin{aligned} &L(\boldsymbol{w},b,\boldsymbol{\xi}, \hat{\boldsymbol{\xi}},\boldsymbol{\mu},\hat{\boldsymbol{\mu}}, \boldsymbol{\alpha},\hat{\boldsymbol{\alpha}})\\ &=\frac{1}{2}||\boldsymbol{w}||^2+C\sum^{N}_{i=1}{(\xi_i+\hat{\xi}_i)}-\sum^{N}_{i=1}(\mu_i \xi_i+\hat{\mu}_i\hat{\xi}_i)\\ &+\sum_{i=1}^{N}\alpha_i(y_i-\boldsymbol{w}^T\boldsymbol{x}_i -b -\varepsilon - \xi_i) + \sum_{i=1}^{N}\hat{\alpha}_i (\boldsymbol{w}^T\boldsymbol{x}_i +b-y_i -\varepsilon -\hat{\xi}_i) \end{aligned}\\

其中 \boldsymbol{\mu},\hat{\boldsymbol{\mu}}, \boldsymbol{\alpha},\hat{\boldsymbol{\alpha}} \geq 0 。

（具体推导步骤可以参考我的 SVM 那篇文章）

那么我们有：

\begin{aligned} \partial_\boldsymbol{w} L&=\boldsymbol{w}-\sum^{N}_{i=1}(\alpha_i-\hat{\alpha}_i)\boldsymbol{x}_i=0\\ \partial_b L&=\sum^{N}_{i=1}(\hat{\alpha}_i-\alpha_i)=0\\ \partial_{\xi_i} L&=C-\mu_i-\alpha_i=0\\ \partial_{\hat{\xi}_i} L&=C-\hat{\mu_i}-\hat{\alpha_i}=0 \end{aligned}\\

将上面等式带入拉格朗日函数，以及写出并利用 KKT 条件可得对偶函数：

\begin{aligned} q(\boldsymbol{\alpha},\hat{\boldsymbol{\alpha}}) &=-\frac{1}{2}\sum^{N}_{i=1}\sum_{j=1}^{N}(\alpha_i-\hat{\alpha}_i)(\alpha_j-\hat{\alpha}_j)\boldsymbol{x}^T_i\boldsymbol{x}_j\\ &-\varepsilon\sum_{i=1}^{N}(\alpha_i+\hat{\alpha}_i)+\sum_{i=1}^{N}y_i(\alpha_i-\hat{\alpha}_i) \end{aligned}\\

KKT 条件如下（分别记为KKT 等式1-4）：

\begin{aligned} \alpha_i(y_i-f(\boldsymbol{x}_i) -\varepsilon - \xi_i) &= 0\\ \hat{\alpha}_i (f(\boldsymbol{x}_i)-y_i -\varepsilon -\hat{\xi}_i) &= 0\\ (C-\alpha_i)\xi_i&=0\\ (C-\hat{\alpha}_i)\hat{\xi}_i&=0\\ \end{aligned}\\

那么有对偶问题如下：

\begin{split} \max_{\boldsymbol{\alpha},\hat{\boldsymbol{\alpha}}} & \; q(\boldsymbol{\alpha},\hat{\boldsymbol{\alpha}})\\ \text{s.t. } & \; \sum^{N}_{i=1}(\hat{\alpha}_i-\alpha_i)=0\\ & \; \boldsymbol{\alpha},\hat{\boldsymbol{\alpha}}\in [0,C] \end{split}\\

对于线性 SVR，则：

\boldsymbol{w}^\ast=\sum^{N}_{i=1}(\alpha_i-\hat{\alpha}_i)\boldsymbol{x}_i\\

f(\boldsymbol{x})=\sum^{N}_{i=1}\left (\alpha_i-\hat{\alpha}_{i}\right )\left \langle \boldsymbol{x}_i, \boldsymbol{x}\right \rangle + b\\

对于非线性 SVR，自然地，引入核函数（kernel function） K(\cdot, \cdot) 即可。

\begin{split} f(\boldsymbol{x})&=\sum^{N}_{i=1}\left (\alpha_i-\hat{\alpha}_{i}\right )\left \langle \varphi(\boldsymbol{x}_i), \varphi(\boldsymbol{x})\right \rangle + b\\ f(\boldsymbol{x})&=\sum^{N}_{i=1}\left (\alpha_i-\hat{\alpha}_{i}\right ) K(\boldsymbol{x}_i, \boldsymbol{x}) + b\\ \end{split}\\

常用的核函数有多项式（Polynomial）核 K(\boldsymbol{x}_i, \boldsymbol{x}_j)=\left \langle \boldsymbol{x}_i,\boldsymbol{x}_j\right \rangle ^d ，高斯径向基函数（Gaussian Radial Basis function） K(\boldsymbol{x}_i, \boldsymbol{x}_j)=\exp(-\frac{\left\|\boldsymbol{x}_i- \boldsymbol{x}_j)\right\|^2}{2\sigma^2}) 等。