对程序耗时的理论分析 |
您所在的位置:网站首页 › vi运行c程序耗时 › 对程序耗时的理论分析 |
对程序耗时的理论分析
|
在用科学方法分析程序中,以 ThreeSum 为例总结了科学方法在分析程序用时中的作用,理论和实验在科学方法中是相互依赖的,前面的例子大多还属于实验的范围,所以下面将建立一个理论模型来解释为什么 ThreeSum.count(a) 的运行时间 \(T(N) = aN^3\)(其中 N 为数组 a 的长度,\(a\) 为常数)。 通常认为,一个程序运行的总时间主要和两点有关: ❏ 执行每条语句的耗时; ❏ 执行每条语句的频率。 前者取决于计算机、Java 编译器和操作系统,后者取决于程序本身和输入。如果对于程序的所有部分我们都知道了这些性质,就可以将它们相乘并将程序中所有指令的成本相加得到总运行时间。 执行频率我们可以根据执行的频率将 ThreeSum.count(int[]) 中的 Java 语句分块: 图 1 程序语句执行频率的分析
其中,语句块 C 的执行频率为从输入数组中能够取得的两个不同整数的数量,语句块 E 的执行频率为从输入数组中能够取得的三个不同整数的数量,可由组合数公式 \(\mathrm{C}_n^m=\frac{n!}{m!(n-m)!}\) 得到。cnt++ 命令的执行的次数为输入中和为 0 的整数三元组的数量,其值取决于输入数据,对于用科学方法分析程序中的 DoublingTest,其输入值是随机产生的,所以我们可用概率分析得到该值的期望,进而得到平均情况下 cnt++ 命令执行的次数,这里我们假设该值为 x。 执行耗时对于语句的耗时,我们用常数 t0、t1、t2... 表示各个代码块的执行时间(假设每个 Java 代码块所对应的机器指令集所需的执行时间都是固定的)。于是可将各语句块的执行频率和耗时汇总如下: 语句块 运行时间(以秒记) 频率 总时间 E t0 x(取决于输入) t0x D t1 N3/6-N2/2+N/3 t1(N3/6-N2/2+N/3) C t2 N2/2-N/2 t2(N2/2-N/2) B t3 N t3N A t4 1 t4 总时间 (t1/6)N3 +(t2/2-t1/2)N2 +(t1/3-t2/2+t3)N +t4+t0x上表统计得到的总时间 T(N)=(t1/6)N3+(t2/2-t1/2)N2+(t1/3-t2/2+t3)N+t4+t0x,根据假设,t0、t1、t2... 都为常数,而现代计算机都很快,所以他们应该都是很小的值,因此在 N 很大的时候,T(N) 首项之后的其他项都相对较小,也就是 T(N) 除以 (t1/6)N3 的结果随着 N 的增大趋向于 1。我们定义: ~f(N) 表示所有随着 N 的增大除以 f(N) 的结果趋近于 1 的函数。g(N)~f(N) 表示 g(N)/f(N) 随着 N 的增大趋近于 1。 于是有 T(N)~(t1/6)N3,即总用时 T(N) 在 N 很大的时候与 (t1/6)N3 相对接近。该结论解释了为什么在用科学方法分析程序中拟合得到的时间成本函数为 \(T(N) = aN^3\)。 T(N) 的首项 (t1/6)N3 是语句块 D 的执行频率的一部分,而 T(N)~(t1/6)N3,从程序的层面来看,这意味着执行最频繁的指令决定了程序执行的总时间——我们将这些指令称为程序的内循环。这种情况是很典型的:许多程序的运行时间都只取决于其中的一小部分指令。 增长数量级在对函数进行近似的时候,一般我们用到的近似方式都是 g(N)~af(N),其中 f(N)=Nb(logN)c,a、b 和 c 均为常数。我们将 f(N) 称为 g(N) 的增长数量级,比如 T(N) 的增长数量级为 N3。我们一般不会指定增长数量级中的底数,因为常数 a 能够弥补这些细节(使用换底公式)。这种形式的函数覆盖了我们在对程序运行时间的研究中经常遇到的几种函数,如表 1 所示(指数级别是一个例外)。 表 1 常见的增长数量级函数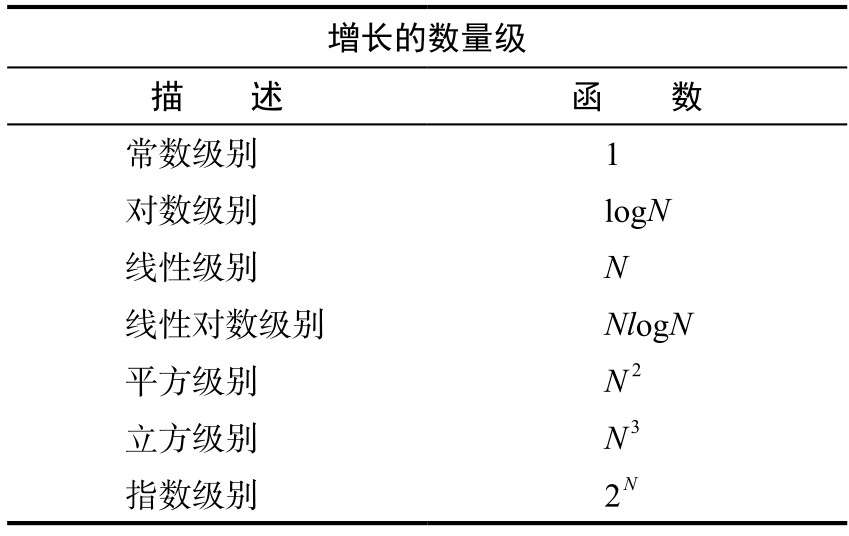 图 2 典型的增长数量级函数
图 2 典型的增长数量级函数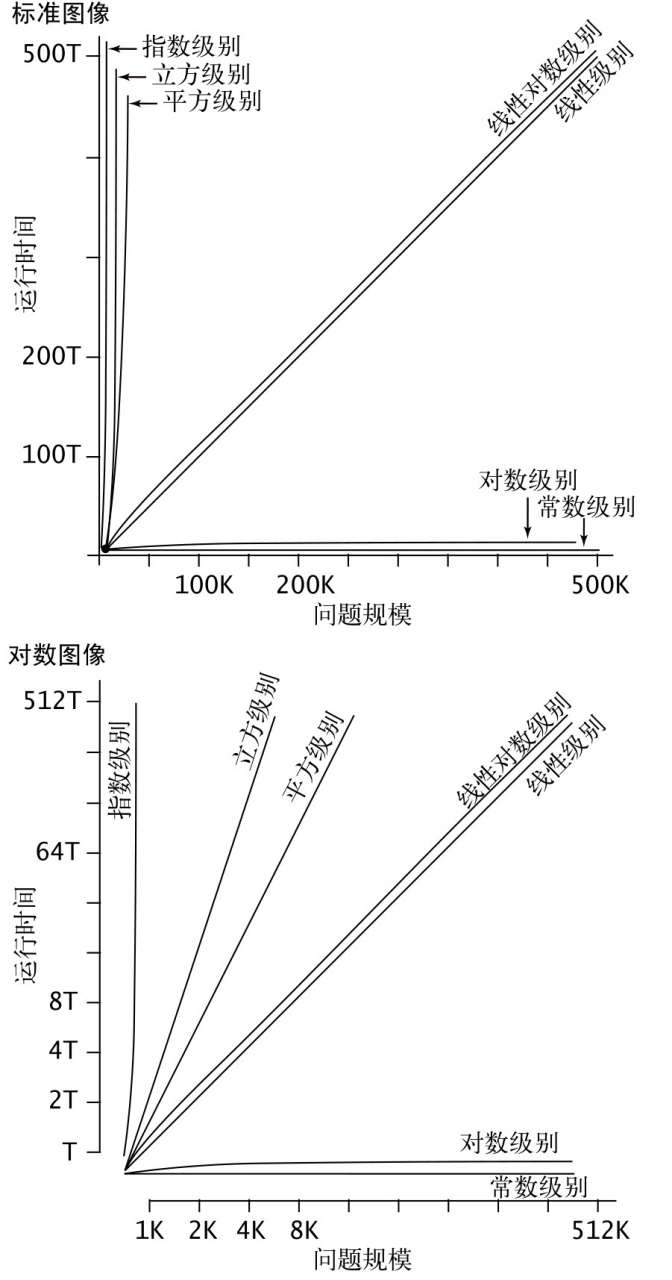
表 1 中的增长数量级函数的增长速度从上至下依次增大(如图 2 所示)。对于函数 f1(x) = ax2 和函数 f2(x) = bx3(a,b 为正常数),不管 a 有多大,b 有多小,当 x 大于 ax2=bx3 的解 x=a/b 时 f2(x) 的图像总是会“追上” f1(x) 的图像,也就是存在 x>a/b 使得 f2(x)>f2(x)。所以 f2(x) 比 f1(x) 增长快。 将其应用到程序分析领域,这意味着一个运行时间的增长数量级为立方级别的程序,其耗时必然会在问题规模足够大时候,超过任何一个耗时的增长数量级为平方级别的程序。也就是增长数量级描述了程序耗时随着问题规模的增长而增长的快慢,比如耗时为常数级别的程序,其耗时不受问题规模 N 的影响而始终是个常数。这就是为什么分析程序时我们最后只得到程序耗时的增长数量级这样一个不含常数的函数——因为常数不重要,增长数量级决定了程序解决大型问题的能力。 所以通常来说,我们最关注的就是程序耗时的增长数量级。可以想象的是,换一种语言(而不改变算法)或者是换一台电脑来写出或执行一个类似的 ThreeSum 程序,最终分析也会得到 T(N)~aN3,其中 a 为一个区别于 t1/6 的常数,他们之间的共性是都有着 N3 的增长数量级,也就是它们解决大型问题的能力是等级别的,因此增长数量级反映了算法的效率,不考虑其他因素的情况下,算法决定了程序解决大型问题的能力。 成本模型由前面的例子,我们知道许多程序的运行时间都只取决于其中的一小部分指令,所以,实际上我们用不着将各语句块的耗时分别加总,通常只需要分析出程序内循环的执行频率,即可得到程序耗时的增长数量级。 另一方面,因为算法决定了耗时的增长数量级,所以我们可通过研究算法来评估一个程序的效率(而不用像前面那样列表格)。 评估算法首先要有一个成本模型,成本模型定义了我们所研究的算法中的基本操作,也就是确定算法中的哪些过程将最为耗时、哪些相对可以忽略,具体到程序上,通常也就是内循环中的操作。所以我们可以按以下过程分析算法/程序: ❏ 确定输入模型,定义问题的规模; ❏ 识别内循环; ❏ 根据内循环中的操作确定成本模型; ❏ 对于给定的输入,判断这些操作的执行频率。这可能需要进行数学分析。 其中输入模型也就是输入数据的状况——输入数据是有序还是无序、是否包含重复项之类。因为不少程序的耗时都是受输入影响的(而且影响可能比较大),所以需要限定输入状况,也就是建立输入模型,作为分析算法的前提。 如果成本模型选择合适,那么指定实现所需的运行时间的增长数量级和它背后的算法的成本的增长数量级应该是相同的。所以假设一个算法的成本的增长数量级是平方级别的,那么我们可以自然地认为指定实现的耗时的增长数量级也是平方级别的,并通过实验进行验证。 比如对于 3-sum 问题的暴力解法(ThreeSum 程序),其输入模型是大小为 N 的数组 a[],内循环是语句块 D,成本模型是对数组的访问,该算法访问了 ~N3/6 个整数三元组中的所有 3 个整数,所以其使用了 ~N3/2 次数组访问来计算 N 个整数中和为 0 的整数三元组的数量。因此我们可以认为 ThreeSum 耗时的增长数量级是立方级别的,可通过实验对其进行验证。 总结自《算法(第四版)》1.4 算法分析 |
【本文地址】
今日新闻 |
推荐新闻 |