t-SNE 算法

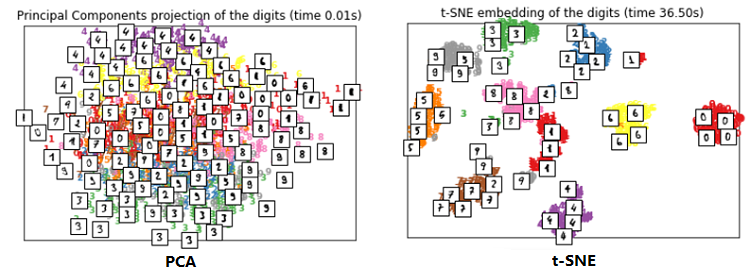
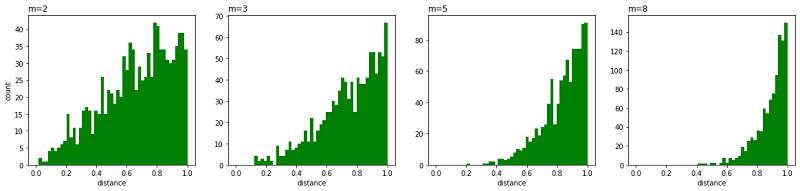
　　t-SNE 即 t-distributed stochastic neighbor embedding 是一种用于降维的机器学习算法，在 2008 年由 Laurens van der Maaten 和 Geoffrey Hinton 提出。

　　t-SNE 是一种非线性降维算法，主要适用于将高维数据降维到 2 维或 3 维 ，方便可视化。但是由于以下种种原因导致它不适合于降维，仅适合可视化：

　　以下使用 t-SNE 和 PCA可视化手写数字的效果对比：

　　常见的降维算法：

　　t-SNE 算法是从 SNE 改进而来，所以先介绍 SNE 。给定一组高维数据 $ \{x_{1}, x_{2}, \ldots, x_{n} \} , x_i=(x_{i}^{(1)}$，$x_{i}^{(2)},x_{i}^{(3)},......x_{i}^{(n)}) $，目标是将这组数据降维到 2 维，SNE 的基本思想是若两个数据在高维空间中是相似的，那么降维到 2 维空间时距离得很近。 

　　随机邻近嵌入（SNE） 采用首先通过将数据点之间的高维欧几里得距离转换为相似性的条件概率来描述两个数据之间的相似性。

　　假设高维空间中的两个点 $ x_{i}, x_{j}$ ，以点 $ x_{i}$ 为中心构建方差为 $ \sigma_{i}$ 的高斯分布。用 $ p_{j \mid i}$ 表示 $ x_{j}$ 在 $ x_{i}$  邻域的概率，若 $ x_{j}$ 与 $ x_{i}$ 相距很近，那么 $ p_{j \mid i}$ 很大；反之， $ p_{j \mid i}$ 很小。

　　$ p_{j \mid i}$ 定义如下：

　　　　$p_{j \mid i}=\frac{\exp \left(-\left\|x_{i}-x_{j}\right\|^{2} /\left(2 \sigma_{i}^{2}\right)\right)}{\sum_{k \neq i} \exp \left(-\left\|x_{i}-x_{k}\right\|^{2} /\left(2 \sigma_{i}^{2}\right)\right)}$

　　只关心不同点对之间的相似度，所以设 $p_{i \mid i}=0$ 。

　　当把数据映射到低维空间后，高维数据点之间的相似性也应该在低维空间的数据点上体现出来。　　

　　假设 $ x_{i}, x_{j}$ 映射到低维空间后对应 $ y_{i}, y_{j}$，那么 $y_{j}$ 是 $ y_{i}$ 邻域的条件概率为 $ q_{j \mid i}$ :

　　　　$q_{j \mid i}=\frac{\exp \left(-\left\|y_{i}-y_{j}\right\|^{2}\right)}{\sum \limits _{k \neq i} \exp \left(-\left\|y_{i}-y_{k}\right\|^{2}\right)}$

　　低维空间中的方差直接设置为  $ \sigma_{i}=\frac{1}{\sqrt{2}}  $ 。同样  $q_{i \mid i}=0$  。 

　　若  $y_{i}$  和  $y_{j}$  真实反映了高维数据点  $x_{i}$  和  $x_{j}$  之间的关系，那么条件概率  $p_{j \mid i}$  与  $q_{j \mid i} $ 应该完全相等。这里只考虑了  $x_{i}$  与  $x_{j}$ 之间的条件概率，若考虑  $x_{i}$  与其他所有点之间的条件概率，则可构成一个条件概率分布  $P_{i}$。 同理在低维空间存在一个条件概率分布  $Q_{i}$  且应该与  $P_{i}$  对应。

　　衡量两个分布之间的相似性采用 KL 距离(Kullback-Leibler Divergence)，SNE 最终目标就是对所有数据点最小化 KL 距 离，我们使用梯度下降算法最小化如下代价函数:

　　　　$C=\sum\limits_{i} K L\left(P_{i}|| Q_{i}\right)=\sum \limits _{i} \sum \limits_{j} p_{j \mid i} \log \frac{p_{j \mid i}}{q_{j \mid i}}$

　　但由于 KL 距离 是一个非对称的度量。最小化代价函数的目的是让  $p_{j \mid i}$  和  $q_{j \mid i}$ 的值尽可能的接近，即低维空间中点的相似性应当与高维空间中点的相似性一致。但从代价函数的形式可以看出，当  $p_{j \mid i}$  较大，$q_{j \mid i}$  较小时，代价较高；而  $p_{j \mid i}$ 较小，$ q_{j \mid i}$ 较大时，代价较低。即高维空间中两个数据点距离较近时，若映射到低维空间后距离较远，那么将得到一个很高的惩罚，这当然没问题。反之，高维空间中两个数据点距离较远时，若映射到低维空间距离较近，将得到一个很低的惩罚值，显然应得到一个较高的惩罚。即SNE的代价函数更关注局部结构，而忽视了全局结构。

　　总结一下SNE的缺点：

　　　　$\frac{\delta C}{\delta y_{i}}=2 \sum \limits _{j}\left(p_{j \mid i}-q_{j \mid i}+p_{i \mid j}-q_{i \mid j}\right)\left(y_{i}-y_{j}\right)$

　　从上图可以看到，随着维度的增大，大部分数据点都聚集在 $m$ 维球的表面附近，与点 $x_i$ 的距离分布极不均衡。如果直接将这种距离关系保留到低维，就会出现拥挤问题。