【计量经济学及Stata应用】第 4 章 一元线性回归 |
您所在的位置:网站首页 › srf计量经济学 › 【计量经济学及Stata应用】第 4 章 一元线性回归 |
【计量经济学及Stata应用】第 4 章 一元线性回归
|
目录
4.1 一元线性回归模型4.2 OLS估计量的推导4.3 OLS的正交性4.4 平方和分解公式4.5 拟合优度4.6 无常数项的回归4.7 一元回归的Stata实例4.8 Stata命令运行结果的存储与调用4.9总体回归函数与样本回归函数:蒙特卡罗模拟
4.1 一元线性回归模型
教育投资的回报率引出 grilic.dta //画两者的散点图,画出回归直线 twoway scatter lnw s||lfit lnw s //“lift”表示“linear fit”,即线性拟合
普通最小二乘法(Ordinary Least Squares,OLS) 我们的任务是:根据观测值——>总体回归直线 1.任意给一条直线
y
i
=
α
^
+
β
^
x
y_i=\hat\alpha+\hat\beta x
yi=α^+β^x 2.残差
e
1
≡
y
i
−
α
^
−
β
^
x
i
e_1\equiv y_i-\hat{\alpha}-\hat{\beta}x_i
e1≡yi−α^−β^xi 残差相加会出现正负相抵的现象,残差绝对值相加不易运算 引出残差平方和 3.残差平方和(Sum of Squared Residuals,SSR)
∑
i
=
1
n
e
i
2
=
∑
i
=
1
n
(
y
i
−
α
^
−
β
^
x
i
)
\sum\limits_{i=1}^n e_i^2=\sum\limits_{i=1}^n(y_i-\hat{\alpha}-\hat{\beta}x_i)
i=1∑nei2=i=1∑n(yi−α^−β^xi) 4.目标:残差平方和最小 OLS的目标函数:
m
i
n
α
^
,
β
^
∑
i
=
1
n
e
i
2
=
∑
i
=
1
n
(
y
i
−
α
^
−
β
^
x
i
)
\mathop{min}\limits_{\hat{\alpha},\hat{\beta}}\sum\limits_{i=1}^n e_i^2=\sum\limits_{i=1}^n(y_i-\hat{\alpha}-\hat{\beta}x_i)
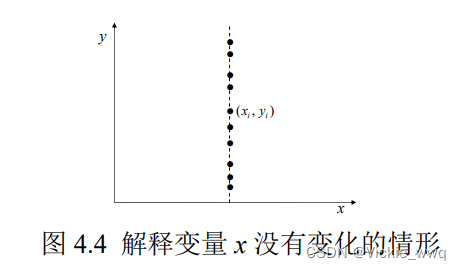
α^,β^mini=1∑nei2=i=1∑n(yi−α^−β^xi) 5.一阶条件 OLS估计量要有意义,分母必须有意义,不为零,解释变量
x
i
x_i
xi是变的,不能是常数。 OLS残差与解释变量及拟合值的正交性是OLS的重要特性 被解释变量 y i y_i yi的“拟合值”(fitted value)或“预测值”(predicted value)为: y ^ ≡ α ^ + β ^ x i \hat{y}\equiv \hat{\alpha}+\hat{\beta}x_i y^≡α^+β^xi 残差写为:
e
i
=
y
i
−
(
α
^
+
β
^
x
i
)
=
y
i
−
y
i
^
e_i=y_i-(\hat{\alpha}+\hat{\beta}x_i)=y_i-\hat{y_i}
ei=yi−(α^+β^xi)=yi−yi^ 被解释变量可分解为相互正交的两个部分,即 y i = y i ^ + e i y_i=\hat{y_i}+e_i yi=yi^+ei 平方差分解公式 前提条件:回归方程有常数项 在证明部分,没有常数项,无法保证残差和等于零 【*我没太懂,细枝末节就先不管了😓】被解释变量的离差平方和TSS=解释平方和ESS+残差平方和SSR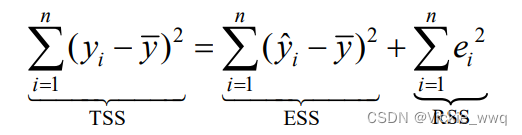  证明:根据OLS的正交性 证明:根据OLS的正交性 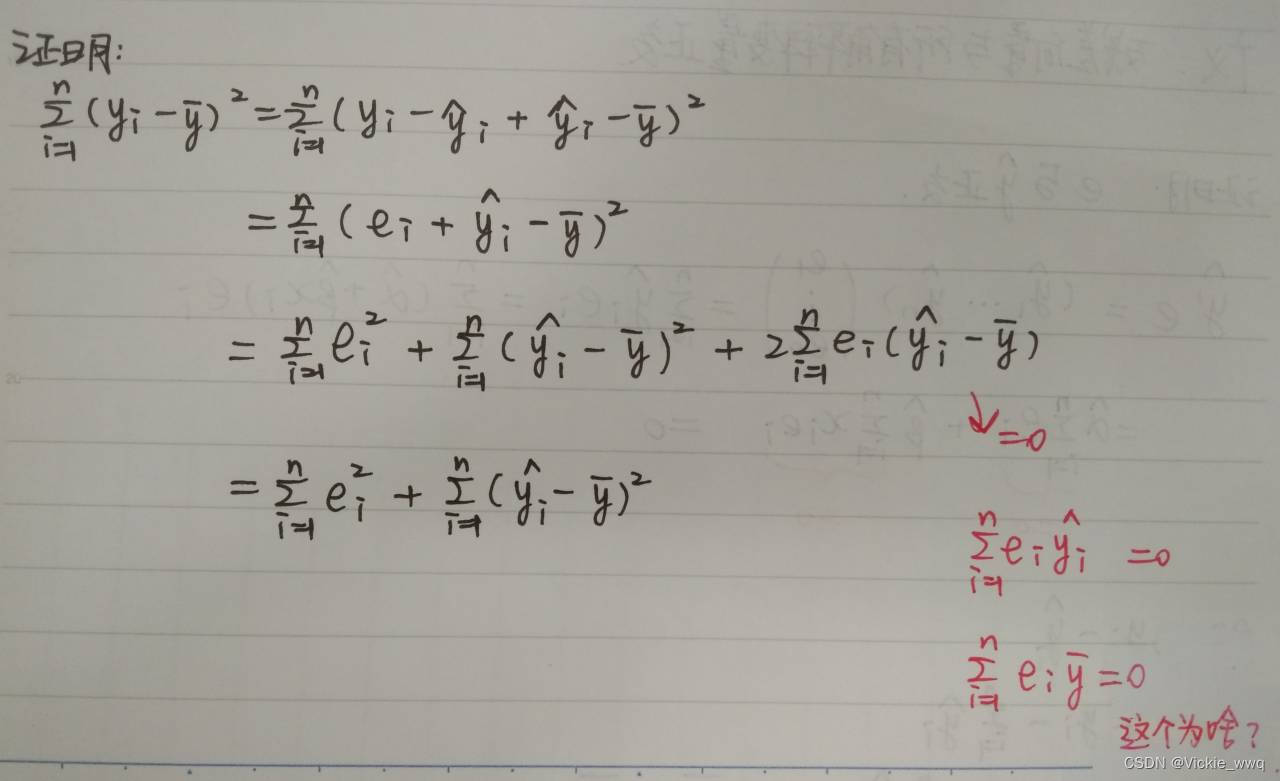 4.5 拟合优度
4.5 拟合优度
在有常数项的情况下,根据平方和分解公式,可将被解释变量的离差平方和分解为模型可以解释与不可解释的部分。显然,如果模型可以解释的部分所占比重越大,则样本回归线的拟合度越好。
由于无常数项的回归必然经过远点,故也称为“经过原点的回归”。此时一元线性回归模型可写为
y
i
=
β
x
i
+
ε
i
(
i
=
1
,
…
,
n
)
y_i=\beta x_i+\varepsilon_i \quad (i=1,…,n)
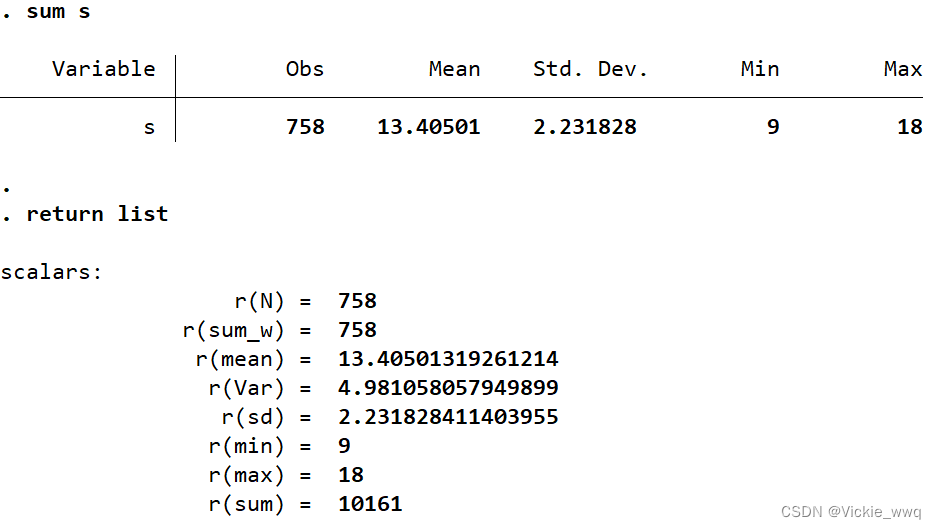
yi=βxi+εi(i=1,…,n) 进行OLS估计,残差平方和最小 grilic.dta //一元回归的命令 regress y x,noconstant //regress简写 reg,"y"是被解释变量,"x"是解释变量,选择项“noconstant”表示无常数项(默认有常数项),简写 noc use grilic.dta,clear reg lnw s
所有的Stata命令可以分为两种e-类命令与r-类命令。 e-类命令(e-class commands)估计命令,比如“regress” e-类命令结果储存在e(),输入ereturn list显示 reg lnw s ereturn list
|
【本文地址】
今日新闻 |
推荐新闻 |
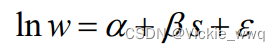
 参数
α
\alpha
α和
β
\beta
β未知,通过样本数据来估计未知参数。
参数
α
\alpha
α和
β
\beta
β未知,通过样本数据来估计未知参数。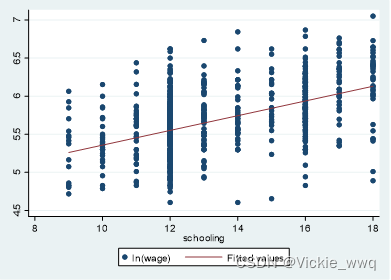


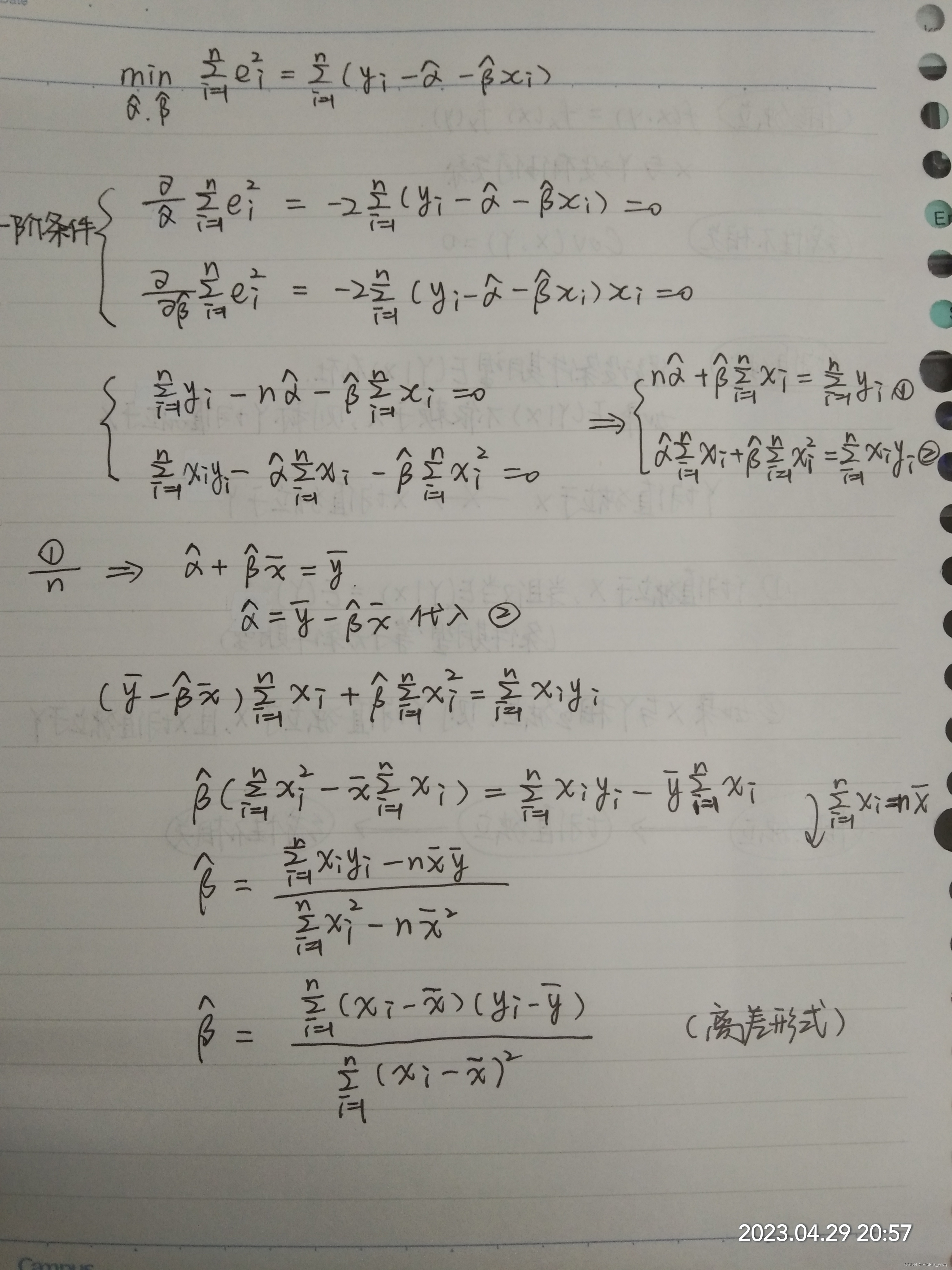
 总体回归函数(Population Regression Function,PRF)
y
=
α
+
β
x
y=\alpha+\beta x
y=α+βx 样本回归函数(Sample Regression Function,SRF)
y
^
=
α
^
+
β
^
x
\hat{y}=\hat{\alpha}+\hat{\beta}x
y^=α^+β^x 样本回归线一定经过
(
x
−
,
y
−
)
(\mathop{x}\limits^-,\mathop{y}\limits^-)
(x−,y−)
总体回归函数(Population Regression Function,PRF)
y
=
α
+
β
x
y=\alpha+\beta x
y=α+βx 样本回归函数(Sample Regression Function,SRF)
y
^
=
α
^
+
β
^
x
\hat{y}=\hat{\alpha}+\hat{\beta}x
y^=α^+β^x 样本回归线一定经过
(
x
−
,
y
−
)
(\mathop{x}\limits^-,\mathop{y}\limits^-)
(x−,y−) 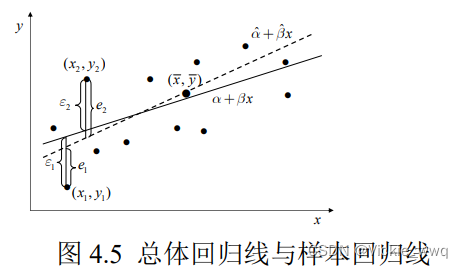

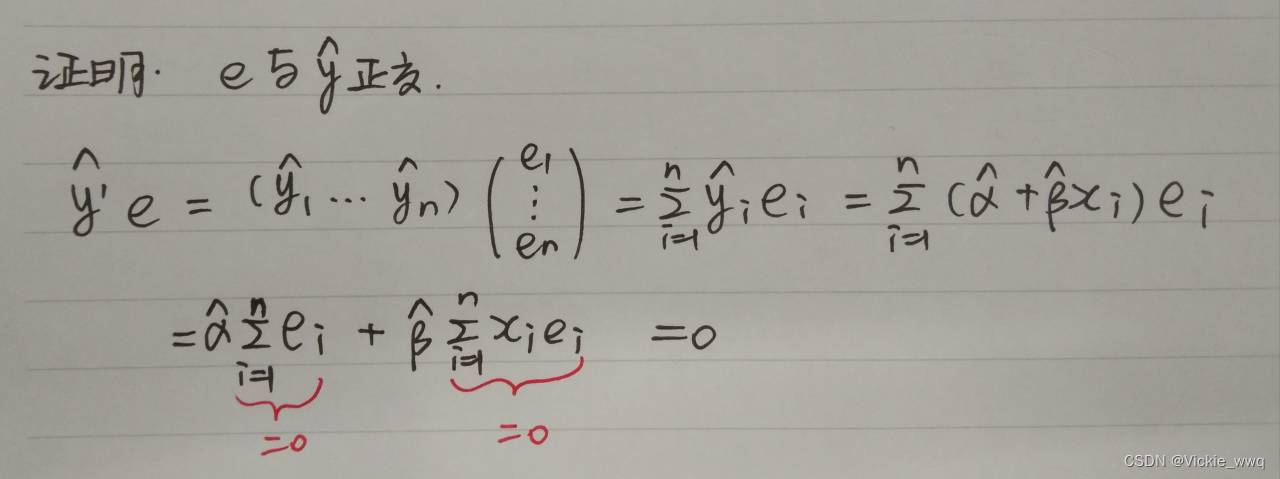 被解释变量的均值恰好等于拟合值的均值,即
y
‾
=
y
^
‾
\overline{y}=\overline{\hat{y}}
y=y^
被解释变量的均值恰好等于拟合值的均值,即
y
‾
=
y
^
‾
\overline{y}=\overline{\hat{y}}
y=y^ 

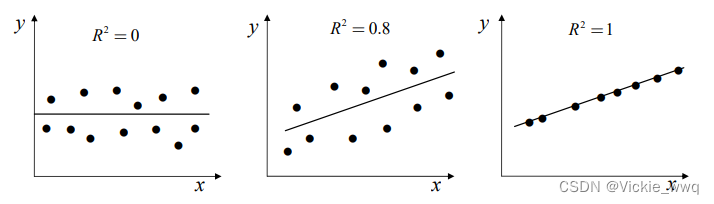 解释一下
R
2
=
0
R^2=0
R2=0的情况:
解释一下
R
2
=
0
R^2=0
R2=0的情况: 
 即使没有常数项,OLS仍满足正交性
即使没有常数项,OLS仍满足正交性  拟合优度 非中心
R
2
R^2
R2 将被解释变量的平方和分成两部分:可由模型解释的部分,模型不可解释的部分
拟合优度 非中心
R
2
R^2
R2 将被解释变量的平方和分成两部分:可由模型解释的部分,模型不可解释的部分 
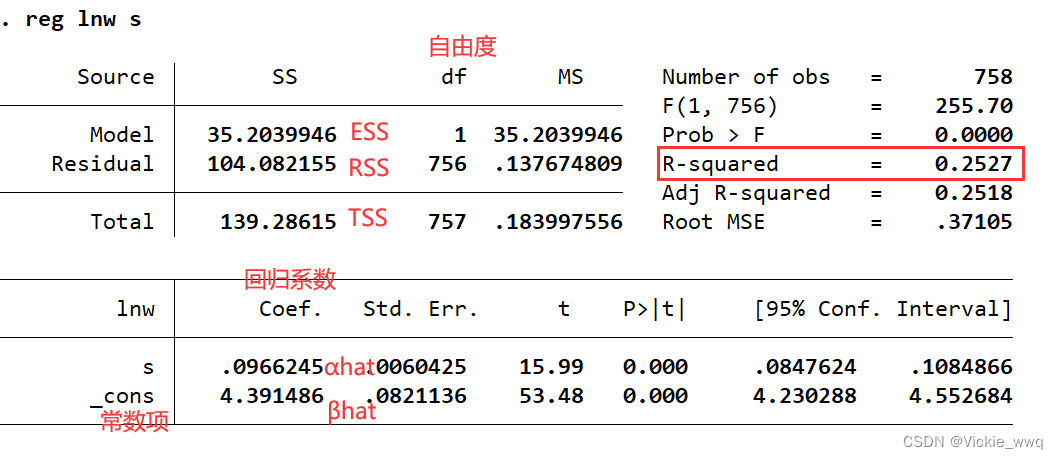 根据结果可将样本回归线写为
l
n
w
^
=
4.391
+
0.097
s
\widehat{lnw}=4.391+0.097s
lnw
=4.391+0.097s 根据一元回归的结果,教育投资的回报率为
9.7
%
9.7\%
9.7%,即每增加一年教育,平均可提高收入
9.7
%
9.7\%
9.7%
根据结果可将样本回归线写为
l
n
w
^
=
4.391
+
0.097
s
\widehat{lnw}=4.391+0.097s
lnw
=4.391+0.097s 根据一元回归的结果,教育投资的回报率为
9.7
%
9.7\%
9.7%,即每增加一年教育,平均可提高收入
9.7
%
9.7\%
9.7%

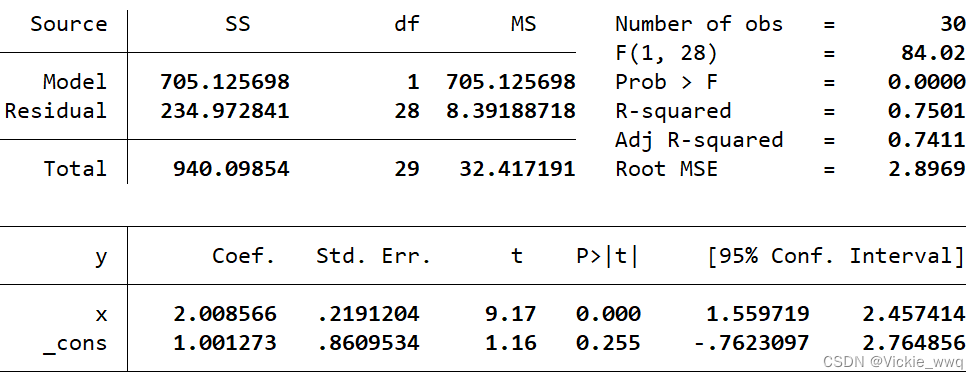
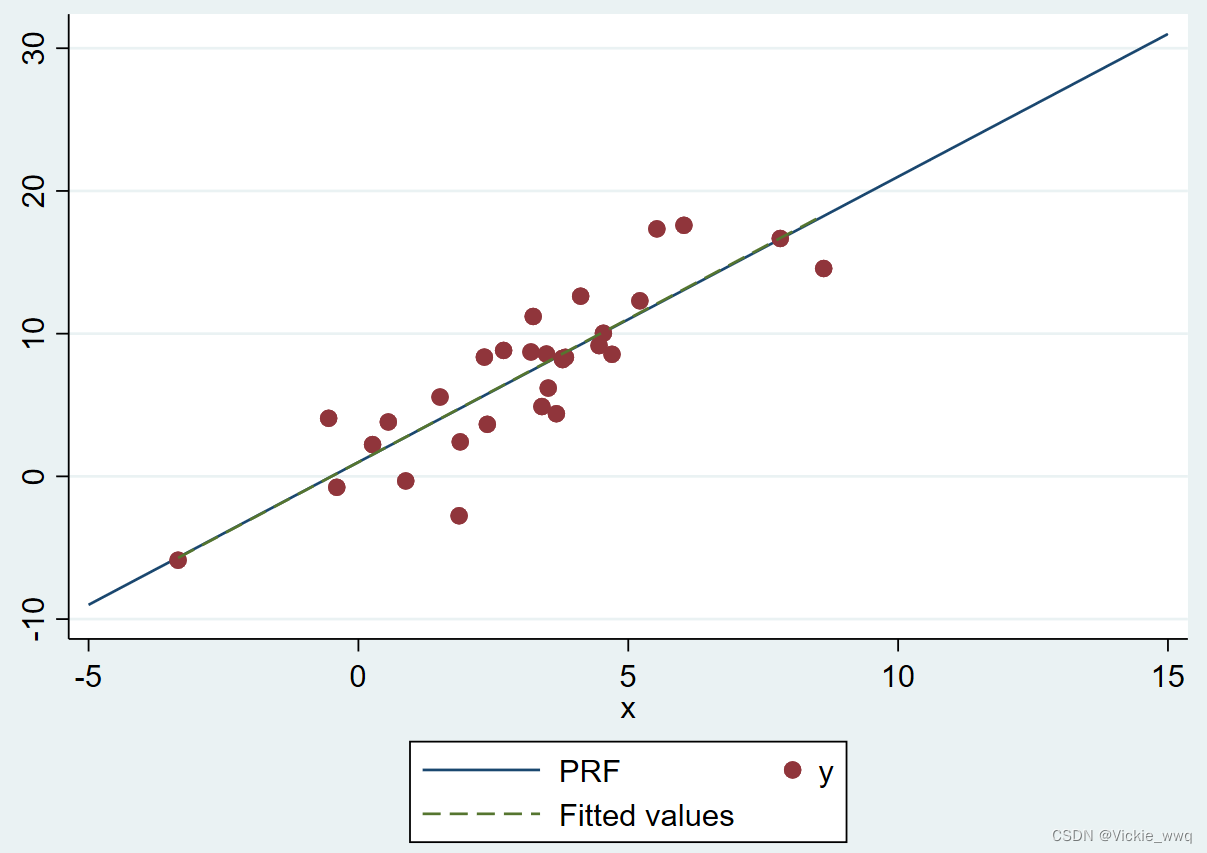 图像两条线重合了,效果不明显
图像两条线重合了,效果不明显