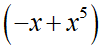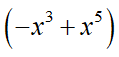/*仅当作学习笔记，若有纰漏欢迎友好交流指正，此外若能提供一点帮助将会十分荣幸*/

前面的几篇博文我们提到提到的都是整数阶模型，这里我们将对分数阶模型进行一个简单的研究。

摘要：与整数阶混沌相比，分数阶混沌更符合、也更接近于现实世界。本文将研究经典Duffing系统的迭代方式、系统参数选择对混沌的影响，并通过MATLAB呈现出其混沌、相图以及庞加莱截面以达到对该系统的全面认识。

目录

0 引言

1 分数阶Duffing系统

1.1系统的构造

1.2 系统混沌图

2 Duffing系统相图

2.1系统相图

2.2系统大周期相图

2.3系统混沌相图

3 Duffing系统庞加莱截面

4 总结

参考文献

分数阶微积分已有300的历史，自然界的物理现象大多以分数阶的形式存在，整数阶微分方程正好是分数阶微分方程的特例.整数阶模型相比，分数阶模型更接近真实的世界，具有更诱人的发展前景，近年来已得到了越来越多的关注值得注意的是，与只有固定翼混沌吸引子的分数阶混沌系统相比，具有多种多翼混沌吸引子共存的分数阶混沌系统显示出更复杂的动力学行为和更好的性能。在安全通信以及图像加密领域，此类分数阶混沌系统具有更高的序列复杂度以及更大的密钥空间，提高了系统安全性能。因此，发现和构造具有多种多翼混沌吸引子共存的低维分数阶混沌系统具有更大的价值，Zhou等人基于四翼整数阶忆阻混沌系统，构造了相应的分数阶忆阻系统，出现三翼与三翼与四翼共存吸引子共存；Xian等人构造了一个双翼与四翼混沌吸引子共存的分数阶混沌系统。目前，构造具有更多种多翼混沌吸引子共存的分数阶系统仍然是一个挑战。

而本文基于经典的Duffing系统，对其进行仿真，得到其混沌、相图以及庞加莱截面，基于此讨论其系统参数对于系统混沌状况的影响。

混沌检测是以混屯系统对参数的敏感性,对噪声的免疫性,周期摄动对混沌的抑制性为基石,从本质上区别于传统的检测方法,突破了原有的限制,达到了极 低的检测门限。因此利用混沌振子检测微弱周期信的方法是近年来兴起的一个新的研究方向，考虑到分数阶系统对微弱信号检测具有独特的优势,采用分数阶混沌系统对间歇故障进行检测,其中经典的Duffing-Homes方程为 :

对于信号检测混沌系统如果其恢复力项由

改为：

则方程变为：

式中阻尼项系数k为0.5 ,构成一个耗散系统。同时适当选取系统的分数阶数可以获得更低的检测门限,将式(2)转化为 : 

式中D表示一阶微分算子D^2则表示二阶微分算子。将分数阶引入方程,将式( 3 ) 中的一阶微分算子变成分数阶,得: 

 由分数算子的性质,可将式(4)转换为含有分数阶的方程组。

采用A. Charef 等人研究的图形逼近方法来进行计算,经过比较采用门限值较低的分数阶系统(即q=0.5)作为检测的混屯系统用来进行幅值检测,其表达式为: 

 针对分数阶数q=0.5、k=0.5、w=1的Duffing系统,其初值选取x=0,x一阶导为0，当系统内置信号振幅γ从小到大发生改变时,系统状态也在周期与混沌状态之间发生着有规律的变化。

根据系统特性设计利用matlab进行迭代，其程序如下：

 得系统中各参数迭代仿真图：

我们可以看到，图中蓝点绘制的‘dz/dt’对应图像出现明显的混沌状况。

在Duffing系统中，不同的状态有不同的相图特征，具有代表性的状态为混沌状态和大尺度周期状态：混沌状态下系统相图曲线混乱，毫无规律可循；在大尺度周期状态下相图曲线规律，相轨迹封闭。

根据1章中的系统的迭代求解，对其改造可以得该系统相图的matlab程序为：

 可得相图：

当系统内置信号振幅γ=0.01时，可到到如下仿真相图：

从仿真图我们可以看到大尺度周期状态下的相图曲线规律，相轨迹封闭。

当系统内置信号振幅γ=0.1时，可到到如下仿真相图：

从仿真图我们可以看到在混沌状态下系统相图曲线混乱。

庞加莱截面(Poincare surface of section)由Poincare于十九世纪末提出，用来对多变量自治系统的运动进行分析。

其基本思想是在多维相空间中适当选取一截面，在此截面上某一对共扼变量取固定值，称此截面为Poincar截面。

观测运动轨迹与此截面的截点( Poincare点)，设它们依次为P1,P2,P3…。原来相空间的连续轨迹在Poincare截面上便表现为一些离散点之间的映射Pn。由它们可得到关于运动特性的信息。如不考虑初始阶段的暂态过渡过程，只考虑Poincare截面的稳态图像，当Poincare截面上只有一个不动点和少数离散点时，可判定运动是周期的;当Poincare截面上是一封闭曲线时，可判定运动是准周期的;当Poincare截面上是成片的密集点，且有层次结构时，可判定运动处于混沌状态。

其matlab程序为：

得到庞加莱图：

而当系统内置信号振幅取0.1时得庞加莱图：

本文以Duffing系统为例，从其混沌状态仿真、相图以及庞加莱截面入手，较为全面的展示了该系统的迭代特性，我们也可以看到系统内置信号振幅γ对系统的影响，当信号振幅γ的值变化时，系统图像也呈现出混沌、大周期的状态。