PID的理解 |
您所在的位置:网站首页 › pid是哪三项 › PID的理解 |
PID的理解
|
PID是简单有效的控制算法,在智能车比赛中多有使用,以下是自己对PID算法的简单总结,重点关注了自己在学习PID时遇到的几个疑惑点 1.基本介绍PID往往都是应用于惰性系统 P:比例,比例项 = 偏差值 x 比例系数 I: 积分,积分项 = 前一段时间的偏差累加起来的平均值 D:微分,微分项 = 前一段时间的偏差变化率 x 微分系数 只看数学推导的话可能多是在连续空间推导,但应用在计算机计算上就必须要看离散化后的的公式 各自的作用: 比例项:用于粗调节和快速调节,是必不可少的,是缩短和目标值之间距离的主要部分,着眼于缩小当下的差距,但会有稳态误差 积分项:用于消除稳态误差,借助先前的经验即把之前的一段时间内的各个偏差累加起来,来消除当下的稳态误差 微分项:用于预判以加快响应,同样是借助先前的经验,但是是通过求先前一段时间内的偏差变化率来预测当下或者下一段时间内偏差的变化趋势,从而早做修正 举个简单的例子: 智能车用到的电磁寻线,装车完成后需要调整电阻值使的采到的AD值在合适的范围。假设需要把其中一个的AD值稳定到2000,当前的值是1000,由此:goal = 2000, now= 1000,偏差error = goal - now = 1000,如果比例系数Kp = 0.2,那么此次调节的比例项为:1000 x 0.2 = 200;先不加其他项,继续下一次调节:goal = 2000, now = 1000 + 200 = 1200, 则error = 800,此次比例项:800 x 0.2 = 160; 下一次:goal = 2000,now = 1200 + 160 = 1360 … 可以看出now的值和goal之间的差值在慢慢减小即比例调节在起作用。另外,观察到以下几点: 1.1 响应速度 当Kp = 0.2时,每次的调节量pout分别是:200, 160, 128, 102, 82 … 当Kp = 0.8时,每次的调节量pout分别是:800, 160, 32, 6.4, 1.28 … 用图像显示为: 可以看出,Kp = 0.8比Kp = 0.2以更快的速度靠近目标值goal 当Kp = 1.5时,每次的调节量pout分别是:1500,-750,375,-187.5,93.75 … 显然和Kp < 1的时候相比,Kp = 1.5时靠近goal的速度更快,但同时出现了很明显的超调,从而引起过大的震荡,很难很快的稳定到goal值附近,效果同样不是很好。 可能会有人说如果Kp = 1.0 呢? 当Kp = 1.0,每次的调节量pout分别是:1000,0,0,0 … 好像十分完美,一次就完成了所有的调节,连后面的积分项和微分项都不用,可事实真的是这样的吗?这个也是我在看PID这方面资料时遇到的一个疑惑点,首先,我们知道,直接Kp = 1.0就完美的实现调节是不可能的,不然我们也没必要花大力气去调节智能车的PID参数了。但是为什么从理论上看这又是那么的完美呢?原因就在于我们开头提到的惰性系统 —— 即系统常常有“惯性”导致调节时会“冲过去一段”从而不能恰好稳定到目标值,也正基于此,我们采使用了PID三项的配合来完成调节。 就拿调节AD值来说:初始值是1000,目标值是2000,刚开始拧电阻会拧的比较快(相当于Kp比较大),因为知道距离目标值还有很远,但拧到1800左右时,会明显放慢拧的速度而慢慢的细调(相当于Kp比较小),到1950附近的时候,则会看着AD值在2000附近跳动,想着利用其“跳动的惯性”使它恰好落到2000上,比如拧动电阻使AD呈增加的趋势时,当示数变成1980后就停止拧动,剩下的20可以依靠系统惯性完成调节。当你眼睛盯着AD值变成2000时立即松手,AD值反而不恰好落在2000,这就是所谓的惰性系统。 所谓惰性系统就是变化比较慢且无法精确控制和调节的对象,最重要的特点就是变化速度慢,调节速度慢,控制周期长。也就是说,你看到示数和实际内部的变化之间并不是完全一致的,两者之间总是存在一个类似于“惯性”的味道。另外,更明显的一个惰性系统就是温度的控制 —— 当温度计示数达到目标值时关闭加热器,由于加热器的预热和水本身传递温度的惰性,水温还会继续上升一段而导致越过了目标值。 1.2 稳态误差 查看变量error的值,发现最后的error总是不等于0(Kp=1.0的那个忽略) 公式简单推导: 简单介绍一下公式以方便更详细解释积分项和微分项 位置式:计算出的结果是全部控制量的大小,即可以把这个计算结果直接输入给系统 增量式:计算出的结果只是控制量的增量,加上前一时刻的值才是输入给系统的值 位置式的连续式: 1.3 积分项 积分项表达式: 可以看出,只要存在偏差值,对其进行积分后的结果就不为0,即积分项就一直存在,它就一直起作用,只有在偏差值为0后,积分项才消失。 积分项虽然能消除静态误差,但也会降低系统的响应速度,增加系统的超调量。 积分常数Ti越大(Ti 的含义是什么?),积分的积累作用越弱,这时系统在过渡时不会产生震荡,减少超调量和提高系统稳定性,但会增加静态误差的消除所需的时间即响应慢了。 积分常数Ti较小时,积分作用较强,这时系统过渡过程中容易产生震荡,但消除偏差所需的时间减少了即响应快了。 1.4 微分项 微分项公式: 有助于减小超调量,克服震荡,加快跟踪速度,提高稳定性。但微分对输入信号的噪声很敏感,对于噪声较大的系统一般不用微分或在微分起作用之前先对信号进行滤波 微分时间常数Td越大,抑制偏差变化的作用越强;反之则作用越弱 1.5 离散化 应用于计算机中。由于计算机中是采样,只能根据采样时刻的偏差计算控制量而不能像模拟控制那样连续输出控制量进行连续控制,因此积分项和微分项不能直接使用,必须进行离散化处理。 离散化处理的方法:以 T 为采样周期,k 作为采样序号,则离散采样时间 kT 对应着连续时间t ,用矩形法数值积分近代替积分,用差分代替微分,作近似变换:
1.5.1 离散代替连续 比如,T=1ms,则1s能采1000个数据,采一个数据只需1ms,采到第 k 个数据时耗时 kT ms,此时这个 kT 就和我们平时说的连续时间t的概念十分接近了 —— t 对应着任意数据所对应的时刻即不论多么细小的时间间隔,比如:数据1是100,对应时刻第 t1 = 0.2ms,数据2是150,对应着第 t2 = 0.200000000002ms(甚至说可以是更小的时间差,因为实际情况是可以无限小而趋于0的,这个无限小的精度其实就说明实际情况是可以连续采样即采样周期可以无限小。而计算机显然无法处理无限小或无限大的数据,因此就只能用有限小的数据近似替代 —— 用相对足够小的采样周期代替无限小的采样周期,从而实现连续模拟量的数字化(产生的误差基本可以忽略了)。这是AD转化的思想。都来源微积分。 积分是无限份数据的求和运算, 每个时刻对应着一个偏差值, 因此,对 e(t) 在 0 到 t 时间内的积分就是把这一段时间内出现的所有 e(t) 数据累加求和,在连续化中,任意时间段内都有无限个点(时刻)即无限个数据 —— "无限个"显然不适合计算机 结合上面引入的采样周期T,这样在一段时间内的点(采样时刻、数据个数)就是有限的了 此外,为了方便访问每个时刻(即离散点),建立了 k 这个索引号( k 是每个点的编号),kT 就表示其对应的时刻点,e(kT) 表示第 k 个点即 kT 时刻对应的偏差值,T*e(kT) 表示小矩形面积(即微元,见定积分定义),因为 e(t) 和时间 t 轴围成的面积才是 e(t) 的累加(或者说积分)的结果!!!! —— 深刻理解微积分! 1.5.3 微分的实现 微分也就是求导(或者说求斜率),纵坐标之差 / 对应的横坐标之差。公式中的分子是相邻两个偏差值的差,则分母自然对应为 1 倍的 T 1.5.4 离散化后的公式(位置式)
上面这个位置式,观察发现,求和部分中的 j 总是从0开始的即从计时开始的时刻,所以每次的输出均与过去状态有关,要把之前产生的所有偏差值进行累加,工作量太大。 这个是增量式的: 乍一看这个表达式十分简单,直接系数各自乘以一下偏差值就行了,但实际操作中还是需要做许多准备工作的 —— 和采样间隔的配合、对采样数据的滤波。接下来,简单展示一下PID在智能车上的使用。 2 .PID应用到智能车上2.1 速度控制 —— PI控制 首先确定采样周期(间隔)T 香农采样定律:为了不失真的复现信号,采样频率至少应大于或等于连续信号最高频率分量的 2 倍。 我们知道,智能车的速度控制是放在中断里面的,即每隔固定的时间 T1 去读取编码器数值来计算当前速度,然后隔另一个固定时间 T2 去计算电机PID来调整电机速度 我这里,速度采样间隔 T1 = 5ms,PID控制程序(包含有速度偏差值计算的程序)的调用间隔 T2 = 5ms,也就是说每隔(5 ms)可以计算一次速度偏差值 e,采样间隔 T = (5 ms) 其次,做好数据的滤波 通过传感器采集的数据通常都需要进行滤波以减少误差,滤波一般都是在源头数据进行,比如测速度时编码器产生的脉冲数 再者,适当调整公式中积分项的 e ( k − 1 ) e(k-1) e(k−1)和微分项中的 e ( k − 2 ) e(k-2) e(k−2) 的值 电机控制中没有微分项,因此只需适当调整积分项即可,公式中用到的是 e ( k − 1 ) e(k-1) e(k−1) 这一个数据,为了反应更灵敏和更稳定,可以尝试用前10个或20个偏差值的和作为 e ( k − 1 ) e(k-1) e(k−1) void pit0_isr() { // 5ms getSpeed(); } void pit1_isr() { // 5ms motorPID(); } void getSpeed() { // static int16 l_filter[4],r_filter[4]; //调用库函数获取编码器脉冲数 Right_count = -LPLD_FTM_GetCounter(FTM1); LPLD_FTM_ClearCounter(FTM1); r_filter[0]=Right_count; //采集源数据时进行的滤波 for (int i = 3; i > 0; i--) r_filter[i] = r_filter[i - 1]; Left_count = LPLD_FTM_GetCounter(FTM2); LPLD_FTM_ClearCounter(FTM2); l_filter[0]=Left_count; //采集源数据时进行的滤波 for (int i = 3; i > 0; i--) l_filter[i] = l_filter[i - 1]; //推测车速 L_CarSpeed = L_CarSpeed*0.15 + 0.85*(0.4*l_filter[0]+0.3*l_filter[1]+0.2*l_filter[2]+0.1*l_filter[3]) * SPEED_F / L_QD_UNIT; //(计数值*计数频率/一米计数值)求出车速转换为M/S R_CarSpeed = R_CarSpeed*0.15 + 0.85*(0.4*r_filter[0]+0.3*r_filter[1]+0.2*r_filter[2]+0.1*r_filter[3]) * SPEED_F / R_QD_UNIT; //求出车速转换为M/S } void motorPID() { //这里给的是固定速度,还没有结合不同赛道元素进行速度的调整,可自行修改 speedGoal = 2.5; //目标车速 //计算速度偏差 L_PreError[0] = (l_setspeed - speedGoal ) *1000;//L_CarSpeed是编码器传回来测得速度m/s R_PreError[0] = (r_setspeed - speedGoal ) *1000; //求出最近20个偏差的总和作为积分项 L_ControlIntegral += L_PreError[0]; R_ControlIntegral += R_PreError[0]; for(i=19;i>0;i--) //对求得得偏差值进行移位保存 { L_PreError[i]=L_PreError[i-1]; R_PreError[i]=R_PreError[i-1]; } //PI公式 L_SpeedControlOutUpdata = KP * L_PreError[0] + KI * L_ControlIntegral; R_SpeedControlOutUpdata = KP * R_PreError[0] + KI * R_ControlIntegral; // 接着要适配好正负和车轮转向的关系后再作为PWM占空比输入给电机 }2.2 舵机控制 —— PD控制 和电机的控制类似:确定采样间隔、进行数据滤波、适当调整微分项 void camera_err() { // 获取摄像头图像并计算偏差值err[] } #define pout0 1350 //舵机中值 void servoPID() { // 根据摄像头图像偏差值确定舵机打角 pout = pout0 - KP * err[0]; dout = (err[0] - err[2])*KD; out= pout - dout ; //向舵机输出此值 }2.3 参数整定 先调Kp,再调其他 3.理解PID的经典小例子小明加水 小明接到这样一个任务:有一个水缸有点漏水(而且漏水的速度还不一定固定不变),要求水面高度维持在某个位置,一旦发现水面高度低于要求位置,就要往水缸里加水。 小明接到任务后就一直守在水缸旁边,时间长就觉得无聊,就跑到房里看小说了,每30分钟来检查一次水面高度。水漏得太快,每次小明来检查时,水都快漏完了,离要求的高度相差很远,小明改为每3分钟来检查一次,结果每次来水都没怎么漏,不需要加水,来得太频繁做的是无用功。几次试验后,确定每10分钟来检查一次。这个检查时间就称为采样周期。 开始小明用瓢加水,水龙头离水缸有十几米的距离,经常要跑好几趟才加够水,于是小明又改为用桶加,一加就是一桶,跑的次数少了,加水的速度也快了,但好几次将缸给加溢出了,不小心弄湿了几次鞋,小明又动脑筋,我不用瓢也不用桶,老子用盆,几次下来,发现刚刚好,不用跑太多次,也不会让水溢出。这个加水工具的大小就称为比例系数。 小明又发现水虽然不会加过量溢出了,有时会高过要求位置比较多,还是有打湿鞋的危险。他又想了个办法,在水缸上装一个漏斗,每次加水不直接倒进水缸,而是倒进漏斗让它慢慢加。这样溢出的问题解决了,但加水的速度又慢了,有时还赶不上漏水的速度。于是他试着变换不同大小口径的漏斗来控制加水的速度,最后终于找到了满意的漏斗。漏斗的时间就称为积分时间。 小明终于喘了一口,但任务的要求突然严了,水位控制的及时性要求大大提高,一旦水位过低,必须立即将水加到要求位置,而且不能高出太多,否则不给工钱。小明又为难了!于是他又开努脑筋,终于让它想到一个办法,常放一盆备用水在旁边,一发现水位低了,不经过漏斗就是一盆水下去,这样及时性是保证了,但水位有时会高多了。他又在要求水面位置上面一点将水缸要求的水平面处凿一孔,再接一根管子到下面的备用桶里这样多出的水会从上面的孔里漏出来。这个水漏出的快慢就称为微分时间。 看到几个问采样周期的帖子,临时想了这么个故事。微分的比喻一点牵强,不过能帮助理解就行了,呵呵,入门级的,如能帮助新手理解下PID,于愿足矣。故事中小明的试验是一步步独立做,但实际加水工具、漏斗口径、溢水孔的大小同时都会影响加水的速度,水位超调量的大小,做了后面的实验后,往往还要修改改前面 4.我遇到的疑惑点3.1.计算机离散化 本质就是微积分思想 3.2.惰性系统 3.3.稳态误差 3.4.PID计算后也相当于归一化 5.matlab代码 clear all N = 30;%计算多少次 P=1;%决定是否加入比例,一定要加比例控制 I=1;%决定是否加入积分 D=0;%决定是否加入微分 容易导致震荡 MODEL = 0; T = 0.01; %采样周期 In=[2,6,8,10];%选多少项进行积分,决定着积分时间常数 Dn=[2,6,8,10];%选多少项进行微分,决定着微分时间常数 goal = 2000; x=0:1:N; now=zeros(4,N); error=zeros(4,N); pout=zeros(4,N);%比例项 iout=zeros(4,N);%积分项 dout=zeros(4,N);%微分项 now(:,1) = 1000; kp = [0.2,0.8,1.0,1.5]; Td = [0.2,1.5]; Ti = [0.5,3.5]; %用的是增量式 for n=1:4 for i=1:1:N error(n,i) = goal - now(n,i); %纯P控制 if P==1 && I==0 && D==0 pout(n,i) = kp(n) .* error(n,i); now(n,i+1) = now(n,i) + pout(n,i); end %% 这一部分用的PID公式不是最简式,而是详细复现了中间的推导过程 if I==1 %偏差累加了多项,求均值 if i |
【本文地址】
今日新闻 |
推荐新闻 |


 个人认为,之所以存在稳态误差,恰恰就在于只通过比例调节最后的值很难恰好落在目标值上
个人认为,之所以存在稳态误差,恰恰就在于只通过比例调节最后的值很难恰好落在目标值上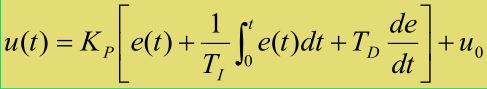 位置式的离散化:
位置式的离散化: 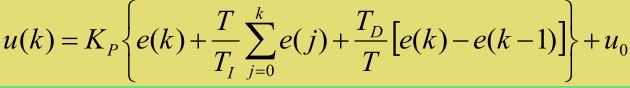 然后可由位置式推导出增量式即总是和上一次的值 u(k-1) 进行比较,直接给出离散化后的
然后可由位置式推导出增量式即总是和上一次的值 u(k-1) 进行比较,直接给出离散化后的 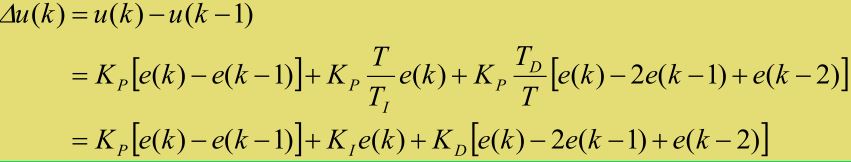 稍作整理,看起来极其简洁
稍作整理,看起来极其简洁 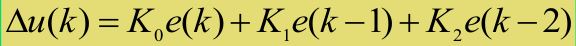
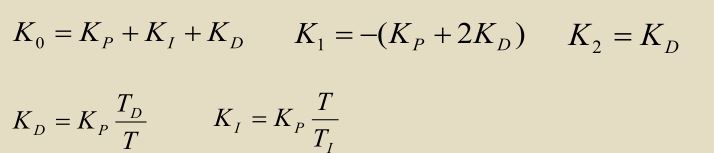 从以上推导过程观察: 1.比例项是必须要存在的,积分项和微分项视需要添加 2.存在积分时间、微分时间这两个常数,这两个常数分别用于调节积分项、微分项的作用强弱,会影响调节的响应速度
从以上推导过程观察: 1.比例项是必须要存在的,积分项和微分项视需要添加 2.存在积分时间、微分时间这两个常数,这两个常数分别用于调节积分项、微分项的作用强弱,会影响调节的响应速度 消除静差,更稳定
消除静差,更稳定 预判,提前调节,以加快响应。
预判,提前调节,以加快响应。 解释:
解释: 1.5.2 积分的实现
1.5.2 积分的实现 这样就能解释第二个公式了 —— 对积分运算进行离散化处理,无限个点的运算转成有限个点的运算来近似代替,从而能用计算机进行快速运算
这样就能解释第二个公式了 —— 对积分运算进行离散化处理,无限个点的运算转成有限个点的运算来近似代替,从而能用计算机进行快速运算 最终可以之表现出
K
p
,
K
i
,
K
d
Kp,Ki,Kd
Kp,Ki,Kd三个系数(也是主要需要调节的参数),其中
K
i
,
K
d
Ki,Kd
Ki,Kd是多个系数综合后的结果
最终可以之表现出
K
p
,
K
i
,
K
d
Kp,Ki,Kd
Kp,Ki,Kd三个系数(也是主要需要调节的参数),其中
K
i
,
K
d
Ki,Kd
Ki,Kd是多个系数综合后的结果 这个的累加就只剩下一个偏差值了,简化了很多,系数同样只剩下了三个
这个的累加就只剩下一个偏差值了,简化了很多,系数同样只剩下了三个