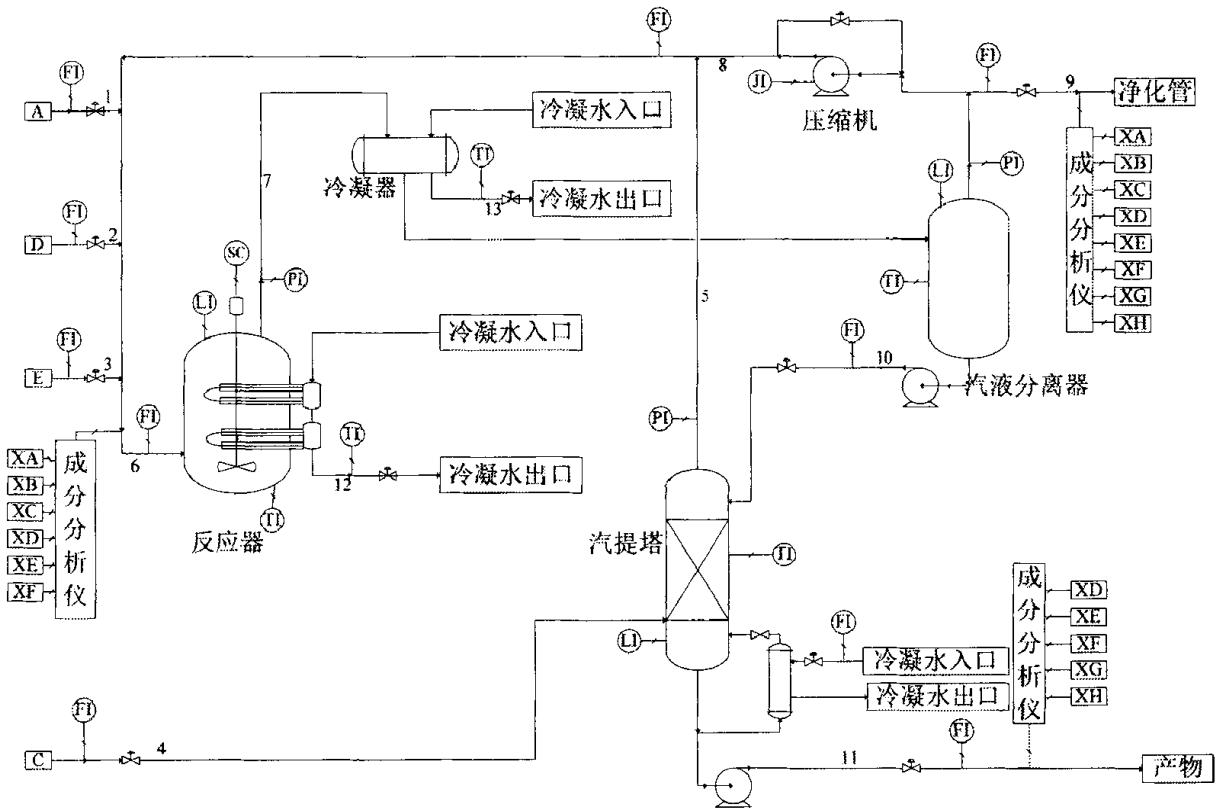
为了提高系统的效率性、可靠性和安全性，一直以来，关于故障检测和分离的研究备受关注。作为过程工业的一部分,化工生产过程是经过化学反应将原料转变成产品的工艺过程。Tennessee-Eastman(TE) 过程是美国 Eastman 化学公司的 Downs & Vogel 于1993年建立的一个实际化工过程的模型,为研究该类过程的故障诊断技术提供了一个实验平台[1]。在生产过程中,一旦发生故障而又不能及时排除时,就会影响生产的进行,并威胁到人员和设备的安全,所以,需要准确及时地识别故障类型并进行相应的处理。目前,化工过程的故障诊断方法主要有模型驱动法和数据驱动法。由于化工过程往往具有慢时变、分布参数、非线性和强耦合特性,难以得到精确的数学模型,使得模型驱动方法的性能不尽理，因此,数据驱动的方法成为处理此类问题的一个重要方向。

在工业过程一类的复杂系统中，系统规模大且过程变量高度耦合，数学机理建模难，这为故障诊断带来了挑战。因而，基于数学机理建模的故障诊断方法不适用于复杂系统。在当前信息时代，系统中的过程数据很丰富且容易获取，从而数据驱动的方法被大量研究以及应用在复杂系统。其中，作为一种数据降维技术，主成分分析法（principal component analysis，PCA）能够提取过程数据中蕴含的强相关关系。PCA 广泛应用于复杂系统的故障诊断。如果检测的数据点大于 PCA 模型所定义的统计限，则判断该数据点为故障数据点，发出系统存在故障的报警。通常选取监控统计量 \(T^2\) 和 \(SPE\) 来进行故障诊断。这两个统计量分别是基于主成分得分和残差定义的。当 PCA 模型检测出故障时，迸一步实施故障分离，确定哪一个或哪几个变量是该故障的主要源头，称之为故障变量，从而帮助操作者根除故障源。通过假设故障变量对监控统计量具有最大的贡献，贡献图（contributionplots）常用于故障分离。本文以 TE 过程作为实验对象，应用基于 PCA 的故障诊断方法进行实验。

本文接下来首先介绍 TE 过程的大致工业流程和数据结构，然后在介绍 PCA 的实现原理的基础上，给出基于 PCA 方法的故障诊断方法的实现方法步骤。

Tennessee-Eastman(TE) 过程是 Downs 等人[1]基于 Tennessee Eastman 化学公司某实际化工生产过程提出的一个仿真系统，其具体流程见下图。在过程系统工程领域的研究中，TE 过程是一个常用的标准问题（benchmark problem），其较好地模拟了实际复杂工业过程系统的许多典型特征，因此被作为仿真例子广泛应用于控制、优化、过程监控与故障诊断的研究中。

TE 过程包含四种气体原料 A、C、D 和 E，两种液态产物 G 和 H，还包含副产物 F 和惰性气体 B，其中进行的不可逆放热化学反应如下：

整个过程主要包含五个操作单元：反应器、冷凝器、循环压缩机、分离器和汽提塔。气态反应物进入反应器，生成液态产物，反应速率服从反应动力学中的 Arrhenius 函数。产物和残余反应物经过冷凝器冷却后进入汽液分离器，分离得到的气体通过压缩机进入循环管道，与新鲜进料混合送入反应器循环使用，分离得到的液体经过管道 10 进入汽提塔进行精制，从汽提塔底得到的流股中主要包含 TE 过程的产物 G 和 H，送至下游过程。TE 过程总共包括12 个操纵变量和 41 个测量变量(包含 22 个连续过程变量和 19 个成分变量)，采用 Lyman 和 Georgakis [2] 提出的过程结构。

TE 过程模拟实际工业过程中常见的 21 种故障模式，这 21 种故障模式的具体描述如表 1 所示。本次实验采用的TE数据集由训练集和测试集组成，数据由 22 次不同的仿真运行数据构成，每个样本都有 53 个观测变量（取 52 个变量时，第 12 个操纵变量 XMV(12) 搅拌速度就不包括在内）。22 次仿真数据每次都分为了训练集样本和测试集样本。正常工况下的训练样本是在 25h 运行仿真下获得的，观测数据总数为 500，而测试样本是在 48h 运行仿真下获得的，观测数据总数为 960 。其余 21 次仿真数据为带有故障的训练集样本，同样分为训练样本和测试样本，每组训练样本\测试样本代表一种故障。带有故障的测试集样本在 48h 运行仿真下获得，其中前 160 个观测值为正常数据，故障在 8h 的时候引入，共采集 960 个观测值。

主成分分析（PCA）法也叫主元分析法，是一种数据降维算法，降维就是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的。在实际的生产和应用中，降维在一定的信息损失范围内，可以为我们节省大量的时间和成本。降维也成为应用非常广泛的数据预处理方法。降维具有的优点有：使得数据集更易使用、降低算法的计算开销、去除噪声、使得结果容易理解。而 PCA 是一种使用最广泛的数据降维算法。

PCA 的主要思想是将 \(n\) 维特征映射到 \(k\) 维空间中，这里的必有 \(k \cdots > \lambda_k > \lambda_{k+1} > \cdots > \lambda_n \]

\(\boldsymbol{p_i}\) 之间是相互正交的单位向量，\(t_i\) 称为第 \(i\) 主元，我们所关心的变量 \(\boldsymbol{x}\) 是一个 \(n\) 维向量，它的一组测量值 \(\boldsymbol{x}(\tau)\) 经过式 \(\eqref{eq:score}\) 变换后得到的值 \(t_i(\tau)\) 称为测量值在第 \(i\) 主元上的得分。主元代表的是变量，而得分是确定值，从几何上解释，主元可以看做是降维后的坐标轴，而得分就是原向量在坐标轴上对应的坐标值。向量 \(\boldsymbol{p_i}\) 被称为第 \(i\) 主元的负荷向量。

PCA 就是求取主元、得分及负荷向量的过程。我们把转换矩阵 \(\boldsymbol{P}\) 称为负荷矩阵，它所长成的 \(k\) 维子空间被称为主元子空间（Principal Component Subspace, PCS），又称模型子空间或表示子空间（Represent Subspace），\(\boldsymbol{T}=\boldsymbol{X P}\) 为由 \(k\) 列得分向量 \([t_i(1),t_i(2),\cdots,t_i(m)]^T\) 组成的矩阵称为得分矩阵，由前面推导结论可以知道，它就是所要求的 \(\boldsymbol{Y}\) 矩阵，只是从不同角度解释而已。后 \(r\) 个主元对应的负荷向量组成的矩阵用 \(\boldsymbol{\overline{P}}\) 表示，被称为残差负荷矩阵，它所张成的 \(r\) 维空间被称为残差子空间（Residual Subspace, RS），即是说 \(\boldsymbol{C}=\left(\boldsymbol{P,\overline{P}}\right)\)。我们可对观测数据矩阵做如下分解，

其中的 \(\boldsymbol{\widehat{X}}_{m\times n}\) 为观测数据矩阵 \(\boldsymbol{X}\) 在 PCS 上的估计或称分量，\(\boldsymbol{R}_{m\times n}\) 为观测数据在残差子空间上的分量，被称为模型的估计残差矩阵。由此可知，通过对正常数据阵 \(\boldsymbol{X}\) 进行 PCA，可以把我们所关心的变量 \(\boldsymbol{x}\) 的观测数据分解为两个子空间的数据，

故障检测就是检测系统中各个监测点的数据有无异常，它通常是将新的观测数据 \(\boldsymbol{x}_{new}\) 与系统校验模型相比较来实现的。跟据两者之间差距的显著性程度，判断系统中有无故障。主元分析法将数据空间分解为主元子空间和残差子空间，每一组观测数据都可以投影到这两个子空间内。因此引入 Hotelling \(T^2\) 和平方预报误差（Squared Prediction Error, SPE）这两个统计量来监测故障的发生。Hotelling \(T^2\) 统计量是用来衡量包含在主元模型中的信息大小，它表示标准分值平方和。它的定义如下，

系统如果正常运行，则 \(T^2\) 应满足

其中，\(T_\alpha\) 为 \(T^2\) 的控制限，\(k\) 为保留的主元数，\(m\) 为样本数，\(1-\alpha\) 是置信度，\(F_\alpha(k, m-k)\) 是服从第一自由度为 \(k\)，第二自由度为 \(m-k\) 的 \(F\) 分布。\(\alpha\) 满足概率公式 \(P\left\{F(m_1,m_2)>F_\alpha(m_1,m_2)\right\}=\alpha\)，在此定义下，\(\alpha\) 取值通常较小的值，如 0.01 左右。

\(SPE\) 统计量也称 \(Q\) 统计量，是通过分析新的观测数据 \(\boldsymbol{x}_{new}\) 的残差进行故障诊断，用以表明这个采样数据在多大程度上符合主元模型，它衡量了这个数据点不能被主元模型所描述的信息量的大小。它的计算如下，

\(SPE\) 的控制限计算公式为，

其中，

且 \(c_\alpha\) 是标准正态分布的置信极限，满足 \(P\{N(0,1)>N_{c_\alpha}(0,1)\}=c_\alpha\)，在此定义下 \(\alpha\) 取值通常也取 0.01 左右。如系统正常运行，则样本的 \(SPE\) 值应该满足 \(SPE SPE if i < 161 SPE_falm = SPE_falm + 1; else cf_SPE = cat(1, cf_SPE, i); end end end fprintf(frecord,'T2,SPE(误报数/误报率/漏报率/延迟诊断时间)：%3d/%.2f/%.2f/%d, %3d/%.2f/%.2f/%d\n',T2_falm,T2_falm/1.6,100-length(xf_T2)/8,xf_T2(1)-161, SPE_falm,SPE_falm/1.6,100-length(cf_SPE)/8,cf_SPE(1)-161); %绘图 figure; % suptitle(['故障模式',num2str(k-1)]); subplot(221); plot(1:n,T2_test,'k'); title('主元分析统计量变化图T2'); xlabel('采样数'); ylabel('T^2'); hold on; line([0,n],[T2UCL1,T2UCL1],'LineStyle','--','Color','r');%画出标志线 line([0,n],[T2UCL2,T2UCL2],'LineStyle','--','Color','g'); subplot(223); plot(1:n,SPE_test,'k'); title('主元分析统计量变化图SPE'); xlabel('采样数'); ylabel('SPE'); hold on; line([0,n],[SPE,SPE],'LineStyle','--','Color','r'); %贡献图 %1.确定造成失控状态的得分 pchs = randsample(cf_SPE,1); fprintf(frecord,'用于计算贡献率的故障点：%d\n',pchs); S = test(pchs,:)*P(:,1:num_pc); r = [ ]; for i = 1:num_pc if S(i)^2/lamda(i) > T2UCL1/num_pc r = cat(2,r,i); end end %2.计算每个变量相对于上述失控得分的贡献 cont = zeros(length(r),52); for i = 1:length(r) for j = 1:52 tmp = abs(S(r(i))/D(r(i))*P(j,r(i))*test(pchs,j)); if tmp < 0 tmp = 0; end cont(i,j) = tmp; end end %3.计算每个变量的总贡献 CONTJ = zeros(52,1); for j = 1:52 CONTJ(j) = sum(cont(:,j)); end %4.计算每个变量对Q的贡献 e = test(pchs,:)*(I - P*P'); contq = e.^2; %5. 绘制贡献图 % figure; subplot(222); bar(CONTJ*100,'k'); title('T^2贡献率'); xlabel('变量号'); ylabel('%'); subplot(224); bar(contq*100,'k'); title('Q贡献率'); xlabel('变量号'); ylabel('%'); end fclose(frecord); 参考

JJ. Downs,E.F. Vogel, A plant-wide industrial process control problem[J]. Computers & Chemical Engineering, 1993. 17(3): p. 245-255.

P.R. Lyman,C. Georgakis, Plant-wide control of the Tennessee Eastman problem[J]. Computers & Chemical Engineering, 1995. 19(3): p. 321-331.

B.M. Wise,N.B. Gallagher, The process chemometrics approach to process monitoring and fault detection[J]. Journal Of Process Control, 1996. 6(6): p. 329 348.

C.F. Alcala, S.J. Qin, Reconstruction-based contribution for process monitoring[J]. Automatica, 2009. 45(7): p. 1593-1600.

Ian T. Jolliffe. Principal component analysis : A beginner’ s guide[J]. Weather, 1993. 48(8): p. 246–253.

Ian. T. Jollife, J. Cadima. Principal component analysis: A review and recent developments[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2016. 374(2065).

刘康玲. 基于自适应PCA和时序逻辑的动态系统故障诊断研究[D].浙江大学,2017.

PCA（主成分分析）原理推导

如何理解拉格朗日乘子法？

机器学习中SVD总结

深入了解PCA

主成分分析（PCA）原理详解

基于PCA的线性监督分类的故障诊断方法-T2与SPE统计量的计算

基于PCA的故障诊断

Han-Sin/PCA-TE