LU分解就是以矩阵的形式记录高斯消元。如果在高斯消元过程中，用到了行交换(碰到了主对角线上的元素为0的情况)，则会反应在LU分解的L矩阵中。

        简而言之，LU分解中的U矩阵保存的是高斯消元的结果，这是不会变的。但，记录消元过程的L矩阵，要么就是把行交换的部分直接放在L矩阵中，这种做法得到的结果就是:

A=LU

        此外，还有一种不用L矩阵记录行交换的方法，那就是用一个个的置换矩阵P去记录行交换操作，这样一来，高斯消元的矩阵表示就是：

PA=LU

        在我的笔记本中，出现过两次PA=LU的学习笔记，这是一个比较新的版本，这是一种非常直观的算法，且里面没有说明P矩阵的表示方式：

 这是一个早期的笔记记录，虽然，他一口气就写出了L,U,P三个矩阵，但我并不推荐。 

        下面用Matlab来验证一下上面的计算结果：

1，先把手动计算出来的结果逐一输入Matlab。

2，分别计算PA和LU，看两者计算结果是否相等。其中，PA表示原始矩阵A经过行交换后得到的结果，而LU表示的是经过高斯消元后的结果U，通过左乘还原矩阵L后得到的结果。

PxA

 LxU

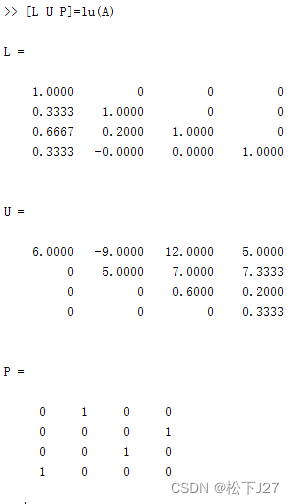
最终得到的等式两端的结果相同，证毕！

         现在，我们再来看看Matlab自带函数lu()的计算结果：

1，首先把我们要进行LU分解的原始矩阵A输进去。

 2，然后用Matlab自带的LU函数进行分解，并同时得到P,L,U三个矩阵。

注意: matlab的计算结果和我们手动计算的结果不同，两种结果都是对的。 

下面我们再补充一个例子：（同样，不推荐这个算法） 

逐一输入L,U,P矩阵：

首先，PA=A，得到经过行交换后的A。

 其次，计算LU，理论上LU的结果应该等于PA，(PA,即经过行交换后的A)。

证毕，礼成！

同样，再看看Matlab自带函数lu()的计算结果:

        以上为matlab的计算结果，这和我们手算出来的不一样。

        虽然我在笔记中对EA的计算进行了详细的说明，但是，当我们在手写L矩阵时，还是不希望在经过这种相对复杂的计算，而是，去尝试，用取巧的办法，直接写出EA的乘积。因为，此时E所乘的矩阵A，不是原始的A矩阵，而是始于单位矩阵I的一系列计算。

        而取巧的办法就是在计算EA时，比如说EijA，只需把Eij对应位置的值，填在A矩阵中的对应位置即可。例如：

或：

（全文完）

作者 --- 松下J27

格言摘抄：

悟道休言天命,修行勿取真经。《遥远的救世主---豆豆》

参考资料(鸣谢)：

1,PA=LU 分解 | 線代啟示錄本文的閱讀等級：中級 令 $latex A&fg=000000$ 是一個 $latex n\times n&fg=000000$ 階可逆矩陣。LU 分解 $latex A=LU&fg=000000$ 是高斯消去法的一種表達形式，下三角矩陣 $latex L=[l_{ij}]&fg=000000$ 記錄消元過程使用的乘數，上三角矩陣 $latex U=[u_{ij}]&fg=000000$ 儲存約化結果，其中 $latex L&fg=000000$ 和 $latex U&fg=000000$ 的主對角元分別滿足 $latex l_{jj}=1&fg=000000$ 和 $latex u_{jj}\neq 0&fg=000000$ (見“LU 分解”)。不過，並非每一可逆矩陣都存在 LU 分解。在執行高斯消去法的化簡程序中，若 $latex 0&fg=000000$ 出現在軸元 (pivot) 位置，即 $latex (j,j)&fg=000000$ 元，列取代運算便無法消去軸元底下各元，這時標準 LU 分解不復存在。可逆矩陣 $latex A&fg=000000$ 的軸元總數 (即 $latex \mathrm{rank}A&fg=000000$) 等於 $latex n&fg=000000$，透過列交換運算必能獲得一個 (非零)…https://ccjou.wordpress.com/2012/04/13/palu-%E5%88%86%E8%A7%A3/

版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27