本节将可逆矩阵的概念和之前学到的一些概念进行了关联，说明了这些概念之间的等价性。最后以空间变换为例，讲述了逆矩阵和逆变换之间的联系。

本节重点讲逆矩阵的概念和第一章中 n n n个未知量 n n n个方程的方程组以及方阵联系起来。 定理：

设 A A A为 n × n n \times n n×n矩阵，则下列命题是等价的，即对某一特定的 A A A，它们同时为真或同时为假： a. A是可逆矩阵 b. A行等价于 n × n n \times n n×n单位矩阵 c. A有 n n n个主元位置 d. 方程 A x = 0 A\boldsymbol x = \boldsymbol 0 Ax=0仅有平凡解 e. A A A的各列线性无关 f. 线性变换 x → A x \boldsymbol x \rightarrow A\boldsymbol x x→Ax是一对一的、 g. 对 R n \mathbb R^n Rn中任意 b \boldsymbol b b，方程 A x = b A\boldsymbol x = \boldsymbol b Ax=b至少有一个解 h. A A A的各列生成 R n \mathbb R^n Rn i. 线性变换 x → A x \boldsymbol x \rightarrow A\boldsymbol x x→Ax把 R n \mathbb R^n Rn映上到 R n \mathbb R^n Rn j. 存在 n × n n \times n n×n矩阵 C C C使 C A = I CA = \boldsymbol I CA=I k. 存在 n × n n \times n n×n矩阵 D D D使 A D = I AD = \boldsymbol I AD=I l. A T A^T AT是可逆矩阵

上述定理的等价性可以一一彼此证明，事实上，如果能够深刻理解之前学习的内容，这些结论是显而易见的，均是同一件事情的不同说法。

例：

应用可逆矩阵定理来判断 A A A是否可逆 A = [ 1 0 − 2 3 1 − 2 − 5 − 1 9 ] A = \begin{bmatrix}1 & 0 & -2 \\ 3 & 1 & -2 \\ -5 & -1 & 9\end{bmatrix} A=⎣⎡​13−5​01−1​−2−29​⎦⎤​

解：

A ∼ [ 1 0 − 2 0 1 4 0 − 1 − 1 ] ∼ [ 1 0 − 2 0 1 4 0 0 3 ] A \sim \begin{bmatrix}1 & 0 & -2 \\ 0 & 1 & 4 \\ 0 & -1 & -1\end{bmatrix} \sim\begin{bmatrix}1 & 0 & -2 \\ 0 & 1 & 4 \\ 0 & 0 & 3\end{bmatrix} A∼⎣⎡​100​01−1​−24−1​⎦⎤​∼⎣⎡​100​010​−243​⎦⎤​ 由于 A A A有3个主元位置，根据上述定理（c）， A A A是可逆的。

一定要注意的是，虽然可逆矩阵定理将许多重要概念作了关联，但必须强调，可逆矩阵定理仅能用于方阵。

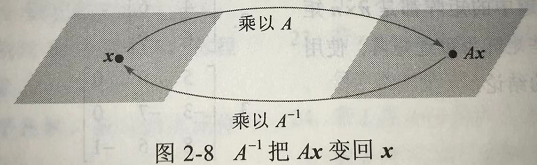
当矩阵 A A A可逆时，方程 A − 1 A x = x A^{-1}A \boldsymbol x = \boldsymbol x A−1Ax=x可看作关于线性变换的一个命题： 线性变换 T : R n → R n T:\mathbb R^n \rightarrow \mathbb R^n T:Rn→Rn称为可逆的，若存在函数 S : R n → R n S:\mathbb R^n \rightarrow \mathbb R^n S:Rn→Rn，使得： 对所有 R n \mathbb R^n Rn中的 x \boldsymbol x x， S ( T ( x ) ) = x S(T(\boldsymbol x)) = \boldsymbol x S(T(x))=x 对所有 R n \mathbb R^n Rn中的 x \boldsymbol x x， T ( S ( x ) ) = x T(S(\boldsymbol x)) = \boldsymbol x T(S(x))=x

下列定理说明若这样的 S S S存在，则它时唯一的而且必是线性变换，我们称 S S S是 T T T的逆，把它写成 T − 1 T^{-1} T−1。 定理：

设 T : R n → R n T:\mathbb R^n \rightarrow \mathbb R^n T:Rn→Rn为线性变换， A A A为 T T T的标准矩阵。则 T T T可逆当且仅当 A A A是可逆矩阵。这时由 S ( x ) = A − 1 x S(\boldsymbol x)=A^{-1}\boldsymbol x S(x)=A−1x定义的线性变换 S S S是满足 S ( T ( x ) ) = x S(T(\boldsymbol x)) = \boldsymbol x S(T(x))=x和 T ( S ( x ) ) = x T(S(\boldsymbol x)) = \boldsymbol x T(S(x))=x的唯一函数。

证：

设 T T T是可逆的，则 T ( S ( x ) ) = x T(S(\boldsymbol x)) = \boldsymbol x T(S(x))=x说明 T T T是从 R n \mathbb R^n Rn映上到 R n \mathbb R^n Rn的映射，因若 b \boldsymbol b b属于 R n \mathbb R^n Rn， x = S ( b ) \boldsymbol x = S(\boldsymbol b) x=S(b)，则 T ( x ) = T ( S ( b ) ) = b T(\boldsymbol x) = T(S(\boldsymbol b)) = \boldsymbol b T(x)=T(S(b))=b，所以每个 b \boldsymbol b b属于 T T T的值域，于是由上述定理(i)， A A A为可逆的。 反之，若 A A A是可逆的，令 S ( x ) = A − 1 x S(\boldsymbol x)=A^{-1}\boldsymbol x S(x)=A−1x，则 S S S是线性变换，且显然 S S S满足 S ( T ( x ) ) = x S(T(\boldsymbol x)) = \boldsymbol x S(T(x))=x和 T ( S ( x ) ) = x T(S(\boldsymbol x)) = \boldsymbol x T(S(x))=x。例如： S ( T ( x ) ) = S ( A x ) = A − 1 ( A x ) = x S(T(\boldsymbol x)) = S(A\boldsymbol x)=A^{-1}(A\boldsymbol x) = \boldsymbol x S(T(x))=S(Ax)=A−1(Ax)=x。于是 T T T是可逆的。

例： 设 T : R n → R n T:\mathbb R^n \rightarrow \mathbb R^n T:Rn→Rn是一对一线性变换，则 T T T会如何？ 解：

T T T的标准矩阵 A A A的列是线性无关的，所以根据可逆矩阵定理， A A A是可逆的，而且 T T T把 R n \mathbb R^n Rn映上到 R n \mathbb R^n Rn，所以， T T T为可逆。

可逆矩阵有两大特性：

正是这两个特性，让可逆矩阵和之前学到的一些概念很好的关联了起来，例如主元位置、线性无关、空间变换等等概念，线性代数中一个主要的任务就是寻找不同概念之间的等价性。