声明：

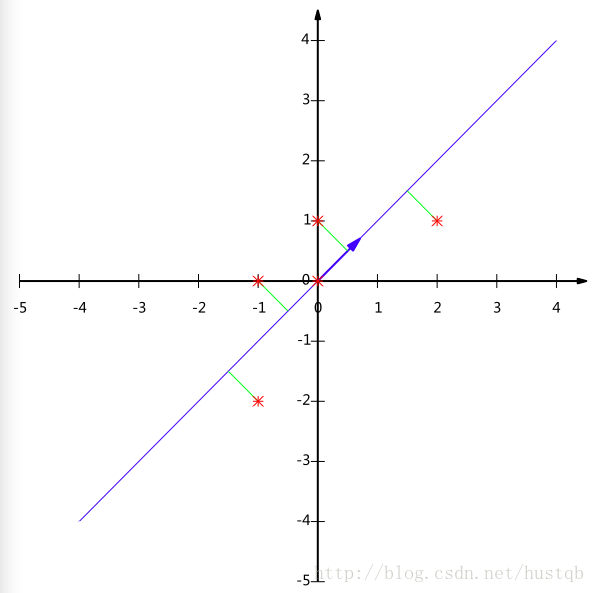
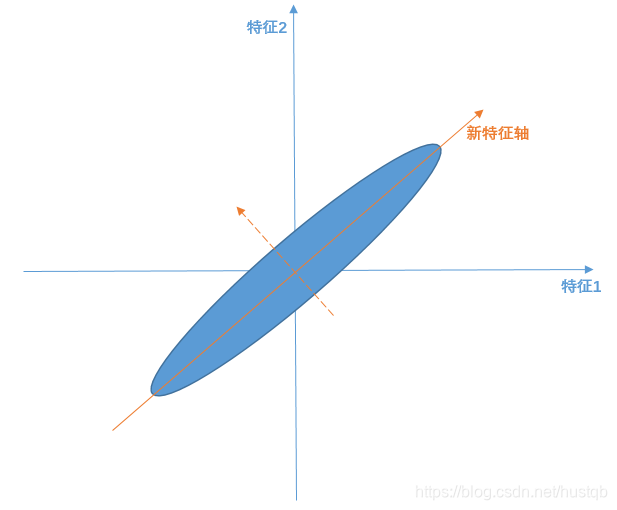
PCA全称Principal Component Analysis，即主成分分析，是一种常用的数据降维方法。它可以通过线性变换将原始数据变换为一组各维度线性无关的表示，以此来提取数据的主要线性分量。 z = w T x z = w^Tx z=wTx   其中，z为低维矩阵，x为高维矩阵，w为两者之间的映射关系。假如我们有二维数据（原始数据有两个特征轴——特征1和特征2）如下图所示，样本点分布为斜45°的蓝色椭圆区域。PCA算法认为斜45°为主要线性分量，与之正交的虚线是次要线性分量（应当舍去以达到降维的目的）。 划重点：

相应的，PCA解释方差并对离群点很敏感：少量原远离中心的点对方差有很大的影响，从而也对特征向量有很大的影响。

一个矩阵与一个列向量A相乘，等到一个新的列向量B，则称该矩阵为列向量A到列向量B的线性变换。

我们希望投影后投影值尽可能分散，而这种分散程度，可以用数学上的方差来表述。 V a r ( a ) = 1 m ∑ i = 1 m ( a i − μ ) 2 Var(a) = \frac 1m \sum_{i=1}^m(a_i - \mu)^2 Var(a)=m1​i=1∑m​(ai​−μ)2即寻找一个一维基，使得所有数据变换为这个基上的坐标表示后，方差值最大。

解释：方差越大，说明数据越分散。通常认为，数据的某个特征维度上数据越分散，该特征越重要。

对于更高维度，还有一个问题需要解决，考虑三维降到二维问题。与之前相同，首先我们希望找到一个方向使得投影后方差最大，这样就完成了第一个方向的选择，继而我们选择第二个投影方向。如果我们还是单纯只选择方差最大的方向，很明显，这个方向与第一个方向应该是“几乎重合在一起”，显然这样的维度是没有用的，因此，应该有其他约束条件——就是正交

解释：从直观上说，让两个字段尽可能表示更多的原始信息，我们是不希望它们之间存在（线性）相关性的，因为相关性意味着两个字段不是完全独立，必然存在重复表示的信息。 字段在本文中指，降维后的样本的特征轴

数学上可以用两个字段的协方差表示其相关性： C o v ( a , b ) = 1 m ∑ i = 1 m ( a i − μ a ) ( b i − μ b ) Cov(a, b) = \frac 1m \sum_{i=1}^m (a_i - \mu_a)(b_i - \mu_b) Cov(a,b)=m1​i=1∑m​(ai​−μa​)(bi​−μb​)当协方差为0时，表示两个字段线性不相关。

总结一下，PCA的优化目标是： 将一组N维向量降为K维（K大于0，小于N），其目标是选择K个单位正交基，使得原始数据变换到这组基上后，各字段两两间协方差为0，而字段的方差则尽可能大。

所以现在的重点是方差和协方差

在统计学上，协方差用来刻画两个随机变量之间的相关性，反映的是变量之间的二阶统计特性。考虑两个随机变量 X i X_i Xi​和 X j X_j Xj​，它们的协方差定义为 c o v ( X i , X j ) = E [ ( X i − E ( X i ) ) ( X j − E ( X j ) ) ] cov(X_i, X_j) = E[(X_i - E(X_i))(X_j - E(X_j))] cov(Xi​,Xj​)=E[(Xi​−E(Xi​))(Xj​−E(Xj​))]

tips：独立，不相关与协方差为零三者的关系 只讨论离散型随机变量的情形。 独立：随机变量 ξ , η \xi ,\eta ξ,η独立是指对于任意的常数a,b，都有 P ( ξ = a , η = b ) = P ( ξ = a ) ⋅ P ( η = b ) P(\xi = a, \eta = b) = P(\xi = a) \cdot P(\eta = b) P(ξ=a,η=b)=P(ξ=a)⋅P(η=b). 相关性，相关系数 ρ ξ η = c o v ( ξ , η ) v a r ( ξ ) v a r ( η ) \rho _{\xi \eta } = \frac {cov(\xi, \eta)}{\sqrt{var(\xi)} \sqrt{var(\eta)}} ρξη​=var(ξ) ​var(η) ​cov(ξ,η)​ 相关系数其实是“线性相关系数” 相关系数和协方差在描述相关性方面是等价的，但独立与相关性的关系是：

协方差矩阵： 假设有m个变量，特征维度为2， a 1 a_1 a1​表示变量1的a特征。那么构成的数据集矩阵为： X = ( a 1 a 2 . . . a m b 1 b 2 . . . b m ) X=\begin{pmatrix} a_1 ; a_2 ;...; a_m\\ b_1 ; b_2 ;...;b_m \end{pmatrix} X=(a1​b1​​a2​b2​​......​am​bm​​)

再假设它们的均值都是0，对于有两个均值为0的m维向量组成的向量组， 1 m X X T = ( 1 m ∑ i = 1 m a i 2 1 m ∑ i = 1 m a i b i 1 m ∑ i = 1 m a i b i 1 m ∑ i = 1 m b i 2 ) \frac 1mXX^T=\begin{pmatrix} \frac 1m \sum_{i=1}^m a_i^2 ; \frac 1m \sum_{i=1}^m a_ib_i\\ \frac 1m \sum_{i=1}^m a_ib_i ; \frac 1m \sum_{i=1}^m b_i^2 \end{pmatrix} m1​XXT=(m1​∑i=1m​ai2​m1​∑i=1m​ai​bi​​m1​∑i=1m​ai​bi​m1​∑i=1m​bi2​​)

可以发现对角线上的元素是两个字段的方差，其他元素是两个字段的协方差，两者都被统一到了一个矩阵——协方差矩阵中。

回顾一下前面所说的PCA算法的目标：方差max，协方差min！！

要达到PCA降维目的，等价于将协方差矩阵对角化：即除对角线外的其他元素化为0，并且在对角线上将元素按大小从上到下排列，这样我们就达到了优化目的。

设原始数据矩阵X对应的协方差矩阵为C，而P是一组基按行组成的矩阵，设Y=PX，则Y为X对P做基变换后的数据。设Y的协方差矩阵为D，我们推导一下D与C的关系： D = 1 m Y Y T = 1 m ( P X ) ( P X ) T = 1 m P X X T P T = P ( 1 m X X T ) P T = P C P T D = \frac 1m YY^T = \frac 1m (PX)(PX)^T = \frac 1m PXX^TP^T = P(\frac 1m XX^T)P^T = PCP^T D=m1​YYT=m1​(PX)(PX)T=m1​PXXTPT=P(m1​XXT)PT=PCPT

解释：想让原始数据集X =>pca成数据集Y，使得Y的协方差矩阵是个对角矩阵。 有上述推导可得，若有矩阵P能使X的协方差矩阵对角化，则P就是我们要找的PCA变换。

优化目标变成了寻找一个矩阵 P P P，满足 P C P T PCP^T PCPT是一个对角矩阵，并且对角元素按从大到小依次排列，那么 P P P的前 K K K行就是要寻找的基，用 P P P的前 K K K行组成的矩阵乘以 X X X就使得 X X X从 N N N维降到了 K K K维并满足上述优化条件。

首先，原始数据矩阵X的协方差矩阵C是一个实对称矩阵，它有特殊的数学性质：

一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量，设这n个特征向量为 e 1 , e 2 , . . . , e n e_1, e_2, ..., e_n e1​,e2​,...,en​，我们将其按列组成矩阵： E = ( e 1   e 2   . . .   e n ) E = (e_1 \ e_2 \ ... \ e_n) E=(e1​ e2​ ... en​) 则对协方差矩阵C有如下结论： E T C E = Λ = ( λ 1 λ 2 . . . λ n ) E^TCE = \Lambda = \begin{pmatrix} \lambda_1 ; ; ; \\ ;\lambda_2 ; ; \\ ; ;... ; \\ ; ; ;\lambda_n \end{pmatrix} ETCE=Λ=⎝⎜⎜⎛​λ1​​λ2​​...​λn​​⎠⎟⎟⎞​这里不懂的朋友可以查阅线性代数相关书籍。 P = E T P = E^T P=ET

P是协方差矩阵的特征向量单位化后按行排列出的矩阵，其中每一行都是C的一个特征向量。如果设P按照中特征值的从大到小，将特征向量从上到下排列，则用P的前K行组成的矩阵乘以原始数据矩阵X，就得到了我们需要的降维后的数据矩阵Y。

在解释一下，特征值 λ \lambda λ为什么要从大到小排列，为什么要选较大的 λ \lambda λ？？？ 因为我们协方差矩阵的对角线元素是方差，我们想要找方差交大的特征维度，所以要选择较大的对角线元素。 而对角矩阵 Λ \Lambda Λ虽然是C经过线性变化后的矩阵，但它在对角线上元素的大小关系没变，特征维度 i i i对应的特征值 λ i \lambda_i λi​越大，该维度上数据的方差越大。

该思路基于拉格朗日问题的求解方法。 回到一开始， z = w T x z=w^Tx z=wTx。其中，最主要的成分是这样的 w 1 w_1 w1​，样本投影到 w 1 w_1 w1​上之后最分散，使得样本点之间的差别变得最明显。为了得到唯一解且是该方向成为最重要的因素，我们要求 ∣ ∣ w 1 ∣ ∣ = 1 ||w_1|| = 1 ∣∣w1​∣∣=1. 如果 z 1 = w 1 T x z_1={w_1}^Tx z1​=w1​Tx且 C o v ( x ) = ∑ Cov(x)=\sum Cov(x)=∑，则 V a r ( z 1 ) = E [ ( w T x − w T μ ) 2 ] = w 1 t ∑ w 1 Var(z_1) =E[(w^Tx - w^T\mu)^2] = {w_1}^t\sum w_1 Var(z1​)=E[(wTx−wTμ)2]=w1​t∑w1​ 寻找 w 1 w_1 w1​，使得 w 1 w_1 w1​在约束下最大化。将这写成拉格朗日问题，则有： max ⁡ w 1 w 1 T ∑ w 1 − α ( w 1 T w 1 − 1 ) \max_{w_1}{w_1}^T\sum w_1 - \alpha(w_1^Tw_1 - 1) w1​max​w1​T∑w1​−α(w1T​w1​−1) 关于 w 1 w_1 w1​求导并让它等于0，有： 2 ∑ w 1 − 2 α w 1 = 0 2\sum w_1 - 2\alpha w_1 = 0 2∑w1​−2αw1​=0 因此， ∑ w 1 = α w 1 \sum w_1 = \alpha w_1 ∑w1​=αw1​ 如果 w 1 w_1 w1​是协方差矩阵 ∑ \sum ∑的特征向量，a是对应的特征值，则上式成立。因为我们想最大化 V a r ( z 1 ) = w 1 T ∑ w 1 = α w 1 T w 1 = α Var(z_1) = w_1^T \sum w_1 = \alpha w_1^Tw_1 = \alpha Var(z1​)=w1T​∑w1​=αw1T​w1​=α 所以为了方差最大，我们选择具有最大特征值的特征向量。因此，主成分是输入样本的协方差矩阵的具有最大特征值 λ 1 = α \lambda_1 = \alpha λ1​=α的特征向量。 第二个主成分 w 2 w_2 w2​也应该是最大化方差，具有单位长度，并且与 w 1 w_1 w1​正交。后一个要求是使得投影后 z 2 = w 2 T x z_2=w_2^Tx z2​=w2T​x与 z 1 z_1 z1​不相关。对于第二个主成分，有 max ⁡ w 2 w 2 T ∑ w 2 − α ( w 2 T w 2 − 1 ) − β ( w 2 T w 1 − 0 ) \max_{w_2} w_2^T \sum w_2 - \alpha(w_2^Tw_2 - 1) - \beta(w_2^Tw_1 - 0) w2​max​w2T​∑w2​−α(w2T​w2​−1)−β(w2T​w1​−0) 最后，该式简化为 ∑ w 2 = α w 2 \sum w_2 = \alpha w_2 ∑w2​=αw2​，这表明 w 2 w_2 w2​应该是 ∑ \sum ∑的具有第二大特征值 λ 2 = α \lambda_2=\alpha λ2​=α的特征向量。类次的，我们可以证明其他维被具有递减特征值的特征向量给出。

总结一下PCA的算法步骤： 设有n条m维数据。

关于PCA的python实现代码可以参考这里，不过ipynb文件可能在github上刷不出来，建议下载下来用jupyter notebook打开。

原始数据集矩阵X： ( 1 1 2 4 2 1 3 3 4 4 ) \begin{pmatrix} 1 ; 1 ; 2 ; 4 ; 2 \\ 1 ; 3 ; 3 ; 4 ; 4 \end{pmatrix} (11​13​23​44​24​)

求均值后： ( − 1 − 1 0 2 0 − 2 0 0 1 1 ) \begin{pmatrix} -1 ; -1 ; 0 ; 2 ; 0 \\ -2 ; 0 ; 0 ; 1 ; 1 \end{pmatrix} (−1−2​−10​00​21​01​)

再求协方差矩阵 C = 1 5 ( − 1 − 1 0 2 0 − 2 0 0 1 1 ) ⋅ ( − 1 − 2 − 1 0 0 0 2 1 0 1 ) = ( 6 5 4 5 4 5 6 5 ) C = \frac 15 \begin{pmatrix} -1 ; -1 ; 0 ; 2 ; 0 \\ -2 ; 0 ; 0 ; 1 ; 1 \end{pmatrix} \cdot \begin{pmatrix} -1 ;-2 \\ -1 ;0 \\ 0 ;0 \\ 2 ;1 \\ 0 ;1 \end{pmatrix} = \begin{pmatrix} \frac65 ;\frac45 \\ \frac45 ;\frac65 \end{pmatrix} C=51​(−1−2​−10​00​21​01​)⋅⎝⎜⎜⎜⎜⎛​−1−1020​−20011​⎠⎟⎟⎟⎟⎞​=(56​54​​54​56​​)

特征值： λ 1 = 2 , λ 2 = 2 5 \lambda_1 = 2, \lambda_2 = \frac 25 λ1​=2,λ2​=52​

对应的特征向量： c 1 ( 1 2 1 2 ) , c 1 ( − 1 2 1 2 ) c1\begin{pmatrix} \frac 1{\sqrt 2}\\ \frac 1{\sqrt 2} \end{pmatrix}, c1\begin{pmatrix} -\frac 1{\sqrt 2}\\ \frac 1{\sqrt 2} \end{pmatrix} c1(2 ​1​2 ​1​​),c1(−2 ​1​2 ​1​​)

标准化（其实不标准化也一样，只是稍显不专业） P = ( 1 2 1 2 − 1 2 1 2 ) P = \begin{pmatrix} \frac 1{\sqrt 2} ;\frac 1{\sqrt 2} \\ -\frac 1{\sqrt 2} ;\frac 1{\sqrt 2} \end{pmatrix} P=(2 ​1​−2 ​1​​2 ​1​2 ​1​​)

选择较大特征值对应的特征向量： ( 1 2 1 2 ) \begin{pmatrix} \frac 1{\sqrt 2} ;\frac 1{\sqrt 2} \end{pmatrix} (2 ​1​​2 ​1​​)

执行PCA变换：Y=PX，得到的Y就是PCA降维后的值数据集矩阵： Y = ( 1 2 1 2 ) ⋅ ( − 1 − 1 0 2 0 − 2 0 0 1 1 ) = ( − 3 2 − 1 2 0 3 2 1 2 ) Y = \begin{pmatrix} \frac 1{\sqrt 2} ;\frac 1{\sqrt 2} \end{pmatrix} \cdot \begin{pmatrix} -1 ; -1 ; 0 ; 2 ; 0 \\ -2 ; 0 ; 0 ; 1 ; 1 \end{pmatrix} = \begin{pmatrix} -\frac 3 {\sqrt 2} ; -\frac 1 {\sqrt 2} ; 0 ; \frac 3 {\sqrt 2} ; \frac 1 {\sqrt 2}\end{pmatrix} Y=(2 ​1​​2 ​1​​)⋅(−1−2​−10​00​21​01​)=(−2 ​3​​−2 ​1​​0​2 ​3​​2 ​1​​)

根据上面对PCA的数学原理的解释，我们可以了解到一些PCA的能力和限制。PCA本质上是将方差最大的方向作为主要特征，并且在各个正交方向上将数据“离相关”，也就是让它们在不同正交方向上没有相关性。

因此，PCA也存在一些限制，例如它可以很好的解除线性相关，但是对于高阶相关性就没有办法了，对于存在高阶相关性的数据，可以考虑Kernel PCA，通过Kernel函数将非线性相关转为线性相关，关于这点就不展开讨论了。另外，PCA假设数据各主特征是分布在正交方向上，如果在非正交方向上存在几个方差较大的方向，PCA的效果就大打折扣了。

最后需要说明的是，PCA是一种无参数技术，也就是说面对同样的数据，如果不考虑清洗，谁来做结果都一样，没有主观参数的介入，所以PCA便于通用实现，但是本身无法个性化的优化。