MPU

#MPU| 来源: 网络整理| 查看: 265

一、四元数1.复数相乘

我们知道，复数的代数表示为 $w=x+yi=\left| w \right|e^{i\theta}$ ，几何意义表示为在二维复平面的一个向量w，对于任意两个复数 $w_{1}=x_{1}+y_{1}i=\left| w_{1} \right|e^{i\theta_{1}}$ ， $w_{2}=x_{2}+y_{2}i=\left| w_{2} \right|e^{i\theta_{2}}$ 相乘得 $w_{3}=(x_{1}+y_{1}i)(x_{2}+y_{2}i)=\left| w_{1}w_{2} \right|e^{i(\theta_{1}+\theta_{2})}$ ，几何意义可表示为既改变 $\omega_{1}$ 模的大小（伸缩），又改变了 $\omega_{1}$ 的幅角（旋转）。可以说 $\omega_{2}$ 是 $\omega_{1}$ 的变换因子。如果我们让 $\omega_{2}$ 的模长为1，即只考虑旋转作用，那么 $\omega_{3}$ 是由 $\omega_{1}$ 经过 $\omega_{2}$ 旋转作用得来。我们利用线代理论，引入复数的实矩阵形式来表示这个过程

$\textbf w_3=\textbf w_1\textbf w_2=\left[\begin{array} {cc|c}x_1&-y_1 \\ y_1&x_1\\\end{array}\right]\left[\begin{array} {cc|c}cos\theta_2&-sin\theta_2 \\ sin\theta_2&cos\theta_2\\\end{array}\right]=\left[\begin{array} {cc|c}x_1cos\theta_2- y_1sin\theta_2&-x_1sin\theta_2-y_1cos\theta_2 \\ y_1cos\theta_2+ x_1sin\theta_2&-y_1sin\theta_2+x_1cos\theta_2\\\end{array}\right]=\left[\begin{array} {cc|c}x_3&-y_3 \\ y_3&x_3\\\end{array}\right]$

但是，这只是向量在二维平面的旋转。如果对于三维向量是否能用乘以一个单位向量来表示旋转，这就引出了四元数。

2.四元数

四元数是由哈密顿在1843年爱尔兰发现的。当时他正研究扩展复数到更高的维次（复数可视为平面上的点）。他不能做到三维空间的例子，但四维则造出四元数。[1] 单位四元数可以充当三维向量旋转时相乘的作用因子。

四元数的表示方法

代数式 $\textbf q=q_0+ q_1\textbf i+q_2 \textbf j+q_3 \textbf k$

实矩阵形式 $\textbf q=\left[\begin{array} {} q_0&-q_{1}&-q_{2}&-q_3\\ q_1&q_0&-q_3&q_2\\ q_2&q_3&q_0& -q_1\\ q_3&-q_2&q_1& q_0 \end{array}\right]$

给定一个用于旋转的单位四元数 $\textbf q=q_0+ q_1\textbf i+q_2 \textbf j+q_3 \textbf k$ 和被旋转的三维向量 $\textbf v$ ，那么要直接用四元数旋转这个向量，则我们首先要构造一个纯四元数 $\textbf p=(\textbf v, 0)$ ，设旋转后的向量为 $\textbf v'$ ，旋转后的向量构造的纯四元数为 $\textbf p'=(\textbf v', 0)$ ，那么 $\textbf p'= \textbf q \textbf p \textbf q^{-1}$ ）。[2]

$\textbf p$ 左乘 $\textbf q$ 相当于把 $\textbf p$ 从3维平面变换到4维空间，再右乘 $\textbf q^{-1}$ 相当于从4维空间再变换到三维平面[3] 。

二、欧拉角

欧拉角是用来唯一地确定定点转动刚体位置的三个一组独立角参量，由章动角θ、进动角ψ和自转角φ组成，为L.欧拉首先提出,故得名。

静态定义：对于在三维空间里的一个参考系，任何坐标系的取向，都可以用三个欧拉角来表现。参考系又称为实验室参考系，是静止不动的。而坐标系则固定于刚体，随着刚体的旋转而旋转。

动态定义：我们也可以给予欧拉角两种不同的动态定义。一种是绕着固定于刚体的坐标轴的三个旋转的复合；另外一种是绕着实验室参考轴的三个旋转的复合。[4]

欧拉角旋转序列(Euler Angle Rotational Sequence)一共有18种顺规，6种绕三条轴的旋转(Tait-Bryan Angle，XYZ,XZY,YXZ,YZX,ZXY,ZYX)，另外12种只绕两条轴的旋转(Proper Euler Angle，XYX,YXY,XZX,ZXZ,YZY,ZYZ，XY,YX,XZ,ZX,YZ,ZY)。一共有18种基础旋转的组合顺序，它们可以旋转出三维的所有旋转状态。所以一共是18种旋转顺规（可以表示所有三维旋转的集合）。[5]

我们可以用旋转矩阵来表示三维向量的旋转过程。这里先自定义一下每次的旋转名称和符号：

绕Z轴旋转：航向角yaw(y)绕Y轴旋转：俯仰角pitch(p)绕X轴旋转：横滚角roll(r)

$R_Z(y)=\left[\begin{array} {} cosy&-siny&0\\ siny&cosy&0\\ 0&0&1\\ \end{array}\right] R_Y(p)=\left[\begin{array} {} cosp&0&sinp\\ 0&1&0\\ -sinp&0&cosp\\ \end{array}\right] R_X(r)=\left[\begin{array} {} 1&0&0\\ 0&cosy&-sinr\\ 0&sinr&cosr\\ \end{array}\right]$

我们以ZYX顺规为例，则ZYX顺规的欧拉角旋转矩阵为

$R_{ZYX}=R_ZR_YR_X=\left[\begin{array} {} cosycosp&cosysinpsinr-sinycosr&cosysinycosy+sinysinr\\ sinycosp&sinysinpsinr+cosycosr&sinysinpcosr-cosysinr\\ -sinp&cospsinr&cospcosr\\ \end{array}\right]$

那么对于三维向量 $\textbf v$ 绕自身的坐标系进行ZYX顺规旋转时，我们只需让 $\textbf v$ 右乘 $R_{ZYX}$ 即可得到旋转后的向量 $\textbf v'$

$\textbf v'=\left[\begin{array} {} x'&y'&z'\\ \end{array}\right]= \textbf vR_{ZYX}= \left[\begin{array} {} x&y&z\\ \end{array}\right] \left[\begin{array} {} cosycosp&cosysinpsinr-sinycosr&cosysinycosy+sinysinr\\ sinycosp&sinysinpsinr+cosycosr&sinysinpcosr-cosysinr\\ -sinp&cospsinr&cospcosr\\ \end{array}\right]$

(左乘是相对固定坐标系，右乘是相对当前坐标系)。[6]

三、四元数与欧拉角1.四元数转旋转矩阵

利用罗德里格旋转公式（Rodrigues公式）可以由四元数求得旋转矩阵[7]

$\begin{equation} R_q=\left[\begin{array}{ccc} {q_{0}^{2}+q_{1}^{2}-q_{2}^{2}-q_{3}^{2}} & {2 q_{1} q_{2}-2 q_{0} q_{3}} & {2 q_{1} q_{3}+2 q_{0} q_{2}} \\ {2 q_{1} q_{2}+2 q_{0} q_{3}} & {q_{0}^{2}-q_{1}^{2}+q_{2}^{2}-q_{3}^{2}} & {2 q_{2} q_{3}-2 q_{0} q_{1}} \\ {2 q_{1} q_{3}-2 q_{0} q_{2}} & {2 q_{2} q_{3}+2 q_{0} q_{1}} & {q_{0}^{2}-q_{1}^{2}-q_{2}^{2}+q_{3}^{2}} \end{array}\right] \end{equation}\\$

2.四元数转欧拉角

四元数转化欧拉角可以先将四元数转换为旋转矩阵，同时欧拉角也可以用旋转矩阵来表示（旋转矩阵在四元数转欧拉角中起到了重要作用，相当于转换的“桥梁”。）

对于同一三维旋转过程，用欧拉角旋转矩阵来表示和四元数旋转矩阵来表示是等价的，即 $R_{ZYX}=R_q$ （欧拉角以ZYX顺规为例）

$\left[\begin{array} {} cosycosp&cosysinpsinr-sinycosr&cosysinycosy+sinysinr\\ sinycosp&sinysinpsinr+cosycosr&sinysinpcosr-cosysinr\\ -sinp&cospsinr&cospcosr\\ \end{array}\right] = \left[\begin{array}{ccc} {q_{0}^{2}+q_{1}^{2}-q_{2}^{2}-q_{3}^{2}} & {2 q_{1} q_{2}-2 q_{0} q_{3}} & {2 q_{1} q_{3}+2 q_{0} q_{2}} \\ {2 q_{1} q_{2}+2 q_{0} q_{3}} & {q_{0}^{2}-q_{1}^{2}+q_{2}^{2}-q_{3}^{2}} & {2 q_{2} q_{3}-2 q_{0} q_{1}} \\ {2 q_{1} q_{3}-2 q_{0} q_{2}} & {2 q_{2} q_{3}+2 q_{0} q_{1}} & {q_{0}^{2}-q_{1}^{2}-q_{2}^{2}+q_{3}^{2}} \end{array}\right]$

对比可得

$y=arctan\frac{2(q_0q_3+q_1q_2)}{q_{0}^{2}+q_{1}^{2}-q_{2}^{2}-q_{3}^{2}}\\ p=arcsin2(q_0q_2-q_1q_3)\\ r=arctan\frac{2(q_0q_1+q_2q_3)}{q_{0}^{2}-q_{1}^{2}-q_{2}^{2}+q_{3}^{2}}\\$

3.欧拉角转四元数

类比欧拉角顺规方式（以ZYX顺规为例），我们将旋转四元数 $\textbf q$ 表示为 $\textbf q_Z\textbf q_Y\textbf q_X$

$\textbf q_Z=cos\frac y2+sin\frac y2\textbf k\\ \textbf q_Y=cos\frac p2+sin\frac p2\textbf j\\ \textbf q_X=cos\frac r2+sin\frac y2\textbf i\\$

至于为何要这样表示，我想前面提到的图片和公式可以告诉你答案（这里请聪明的你自己意会）

$\textbf p'= \textbf q \textbf p \textbf q^{-1}\\$

把 $\textbf q_Z\textbf q_Y\textbf q_X$ 分别转换为实矩阵形式

$\textbf q_Z=\left[\begin{array} {} cos\frac y2&0&0&-sin\frac y2\\ 0&0&-sin\frac y2&0\\ 0&sin\frac y2&cos\frac y2&0\\ sin\frac y2&0&0& cos\frac y2 \end{array}\right]\\ \textbf q_Y=\left[\begin{array} {} cos\frac p2&0&-sin\frac p2&0\\ 0&cos\frac p2&0&sin\frac p2\\ sin\frac p2&0&cos\frac p2&0\\ 0&-sin\frac p2& 0&cos\frac p2 \end{array}\right]\\ \textbf q_X=\left[\begin{array} {} cos\frac r2&-sin\frac r2&0&0\\ sin\frac r2&cos\frac r2&0&0\\ 0&0&cos\frac r2&-sin\frac r2\\ 0&0& sin\frac r2&cos\frac p2 \end{array}\right]\\$

$\textbf q=\textbf q_Z\textbf q_Y\textbf q_X=\left[\begin{array} {} cos\frac y2&0&0&-sin\frac y2\\ 0&0&-sin\frac y2&0\\ 0&sin\frac y2&cos\frac y2&0\\ sin\frac y2&0&0& cos\frac y2 \end{array}\right]\left[\begin{array} {} cos\frac p2&0&-sin\frac p2&0\\ 0&cos\frac p2&0&sin\frac p2\\ sin\frac p2&0&cos\frac p2&0\\ 0&-sin\frac p2& 0&cos\frac p2 \end{array}\right]\left[\begin{array} {} cos\frac r2&-sin\frac r2&0&0\\ sin\frac r2&cos\frac r2&0&0\\ 0&0&cos\frac r2&-sin\frac r2\\ 0&0& sin\frac r2&cos\frac p2 \end{array}\right]$

$\textbf q=\left[\begin{array} {} c1c2c3+s1s2s3&s1s2c3-c1c2s3&-c1s2c3-s1c2s3&c1s2s3-s1c2c3\\ c1c2s3 -s1s2c3&c1c2c3+s1s2s3&c1s2s3-s1c2c3&c1s2c3+s1c2s3\\ c1s2c3+s1c2s3&s1c2c3-c1s2s3&c1c2c3+s1s2s3&s1s2c3-c1c2s3\\ s1c2c3-c1s2s3&-c1s2c3-s1c2s3&c1c2s3 -s1s2c3&c1c2c3+s1s2s3 \end{array}\right]$

其中 $c1=cos\frac y2 \\ s1=sin\frac y2 \\ c2=cos\frac p2 \\ s2=sin\frac p2 \\ c3=cos\frac r2 \\ s3=sin\frac r2 \\$

再与实矩阵形式 $\textbf q=\left[\begin{array} {} q_0&-q_{1}&-q_{2}&-q_3\\ q_1&q_0&-q_3&q_2\\ q_2&q_3&q_0& -q_1\\ q_3&-q_2&q_1& q_0 \end{array}\right]$ 对比得

$\textbf q=c1c2c3+s1s2s3+ (c1c2s3 -s1s2c3)\textbf i+(c1s2c3+s1c2s3) \textbf j+(s1c2c3-c1s2s3) \textbf k$

四、mpu6050计算姿态角

其实我们主要是想通过MPU6050得到欧拉角和四元数（可以用算法实现，但是比较复杂）。要通过MPU6050得到四元数和欧拉角，这个过程有两种方法，一种是用原始数据（三轴加速度，三轴角速度），通过一些（卡尔曼滤波、积分运算、减少误差零点漂移等）姿态融合算法转化即可。另一种直接用MPU6050内部的自带的数字运动处理器（即DMP）。DMP就是对三轴加速度计和三轴陀螺仪的ADC数据进行融合计算，得出四元数，再利用四元数计算姿态角。想要实现DMP一般有2种方式：硬件DMP和软件DMP。

1.硬件DMP

我们要用这个DMP功能的话，就要实现加载固件。

那么DMP怎么拿呢，Invensense公司有提供了一个MPU6050的嵌入式运动驱动库，进而我们可以通过这个库移植很方便得出欧拉角。不过Invensense公司提供的MPU6050运动驱动库是基于MSP430芯片的，需要将其移植到其他芯片上，（比如STM32F1系列），当然就要移植修改代码了。[8]

2.软件DMP

在此之前，我们先来看前面的欧拉角旋转矩阵

$R_{ZYX}=\left[\begin{array} {} cosycosp&cosysinpsinr-sinycosr&cosysinycosy+sinysinr\\ sinycosp&sinysinpsinr+cosycosr&sinysinpcosr-cosysinr\\ -sinp&cospsinr&cospcosr\\ \end{array}\right]$

不过要想用欧拉角解算姿态，我们还需要结合欧拉角微分方程[9]（mpu6050输出的是六轴数据，除了三轴加速度，还有三轴角速度，这六个数据是都要用上）

上式中左侧，是本次更新后的欧拉角，对应roll、pitch、yaw。右侧，是上个周期测算出来的角度，三个角速度为mpu6050输出的在这个周期内的角速度，因此求解这个微分方程就能解算出当前的欧拉角。前面介绍了什么是欧拉角，而且欧拉角微分方程解算姿态关系简单明了，概念直观容易理解，那么我们为什么不用欧拉角来表示旋转而要引入四元数呢？

一方面是因为欧拉角微分方程中包含了大量的三角运算，这给实时解算带来了一定的困难。而且当俯仰角为90度时方程式会出现GimbalLock（万向锁）现象。所以欧拉角方法只适用于水平姿态变化不大的情况，而不适用于全姿态的姿态确定。四元数法只求解四个未知量的线性微分方程组，计算量小，易于操作，是比较实用的工程方法。

在软件解算中，我们要首先把加速度计采集到的值(三维向量)转化为单位向量，即向量除以模，传入参数是陀螺仪x、y、z值和加速度计x、y、z值：

void IMUupdate(float gx, float gy, float gz, float ax, float ay, float az) { float norm; float vx, vy, vz; float ex, ey, ez; norm = sqrt(axax + ayay + azaz); ax = ax / norm; ay = ay / norm; az = az / norm;

下面把四元数换算成方向余弦中的第三行的三个元素。刚好vx、vy、vz 。其实就是上一次的欧拉角（四元数）的机体坐标参考系换算出来的重力的单位向量。

vx = 2(q1q3 - q0q2); vy = 2*(q0q1 + q2q3); vz = q0q0 - q1q1 - q2q2 + q3q3;

axyz是机体坐标参照系上，加速度计测出来的重力向量，也就是实际测出来的重力向量。axyz是测量得到的重力向量，vxyz是陀螺积分后的姿态来推算出的重力向量，它们都是机体坐标参照系上的重力向量。那它们之间的误差向量，就是陀螺积分后的姿态和加计测出来的姿态之间的误差。向量间的误差，可以用向量叉积（也叫向量外积、叉乘）来表示，exyz就是两个重力向量的叉积。这个叉积向量仍旧是位于机体坐标系上的，而陀螺积分误差也是在机体坐标系，而且叉积的大小与陀螺积分误差成正比，正好拿来纠正陀螺。（你可以自己拿东西想象一下）由于陀螺是对机体直接积分，所以对陀螺的纠正量会直接体现在对机体坐标系的纠正。

ex=（ayvz-azvy）; ey=（azvx-axvz）; ez=（axvy-ayvx）;

用叉积误差来做PI修正陀螺零偏

exInt = exInt + exKi; eyInt = eyInt + eyKi; ezInt = ezInt + ezKi; // adjusted gyroscope measurements gx = gx + Kpex + exInt; gy = gy + Kpey + eyInt; gz = gz + Kpez + ezInt;

四元数微分方程，其中T为测量周期，为陀螺仪角速度，以下都是已知量，这里使用了一阶龙格库塔法[10]求解四元数微分方程：

q0 = q0 + (-q1gx - q2gy - q3gz)halfT; q1 = q1 + (q0gx + q2gz - q3gy)halfT; q2 = q2 + (q0gy - q1gz + q3gx)halfT; q3 = q3 + (q0gz + q1gy - q2gx)halfT;

最后根据四元数方向余弦阵和欧拉角的转换关系，把四元数转换成欧拉角；即利用前面的公式 $y=arctan\frac{2(q_0q_3+q_1q_2)}{q_{0}^{2}+q_{1}^{2}-q_{2}^{2}-q_{3}^{2}}\\ p=arcsin2(q_0q_2-q_1q_3)\\ r=arctan\frac{2(q_0q_1+q_2q_3)}{q_{0}^{2}-q_{1}^{2}-q_{2}^{2}+q_{3}^{2}}\\$

所以有：

ANGLE.Yaw = atan2(2 * q1 * q2 + 2 * q0 * q3, -2 * q2q2 - 2 * q3q3 + 1)* 57.3; // yaw转换为度数 ANGLE.Y= asin(-2 * q1 * q3 + 2 * q0* q2)* 57.3; // pitch ANGLE.X= atan2(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2* q2 + 1)* 57.3; // roll

完整程序

//变量定义　　#define Kp1 00.0f//比例增益支配率收敛到加速度计/磁强计　　#define Ki 0.002f//积分增益支配率的陀螺仪偏见的衔接　　#define halfT 0.001f//采样周期的一半　　float q0=1，q1=0，q2=0，q3=0;//四元数的元素，代表估计方向　　float exInt=0，eyInt=0，ezInt=0;//按比例缩小积分误差　　float Yaw，Pitch，Roll;//偏航角，俯仰角，翻滚角　　voidIMUupdate（float gx，float gy，float gz，float ax，float ay，float az）　　{ 　　float norm; 　　float vx，vy，vz; 　　float ex，ey，ez; 　　//测量正常化　　norm=sqrt（ax*ax+ay*ay+az*az）; 　　ax=ax/norm;//单位化　　ay=ay/norm; 　　az=az/norm; 　　//估计方向的重力　　vx=2*（q1*q3-q0*q2）; 　　vy=2*（q0*q1+q2*q3）; 　　vz=q0*q0-q1*q1-q2*q2+q3*q3; 　　//错误的领域和方向传感器测量参考方向之间的交叉乘积的总和　　ex=（ay*vz-az*vy）; 　　ey=（az*vx-ax*vz）; 　　ez=（ax*vy-ay*vx）; 　　//积分误差比例积分增益　　exInt=exInt+ex*Ki; 　　eyInt=eyInt+ey*Ki; 　　ezInt=ezInt+ez*Ki; 　　//调整后的陀螺仪测量　　gx=gx+Kp*ex+exInt; 　　gy=gy+Kp*ey+eyInt; 　　gz=gz+Kp*ez+ezInt; 　　//整合四元数率和正常化　　q0=q0+（-q1*gx-q2*gy-q3*gz）*halfT; 　　q1=q1+（q0*gx+q2*gz-q3*gy）*halfT; 　　q2=q2+（q0*gy-q1*gz+q3*gx）*halfT; 　　q3=q3+（q0*gz+q1*gy-q2*gx）*halfT; 　　//正常化四元　　norm=sqrt（q0*q0+q1*q1+q2*q2+q3*q3）; 　　q0=q0/norm; 　　q1=q1/norm; 　　q2=q2/norm; 　　q3=q3/norm; 　　Pitch=asin（-2*q1*q3+2*q0*q2）*57.3;//pitch，转换为度数　　Roll=atan2（2*q2*q3+2*q0*q1，-2*q1*q1-2*q2*q2+1）*57.3;//rollv 　　Yaw=atan2（2*（q1*q2+q0*q3），q0*q0+q1*q1-q2*q2-q3*q3）*57.3;//Yaw 　　}

封面[11]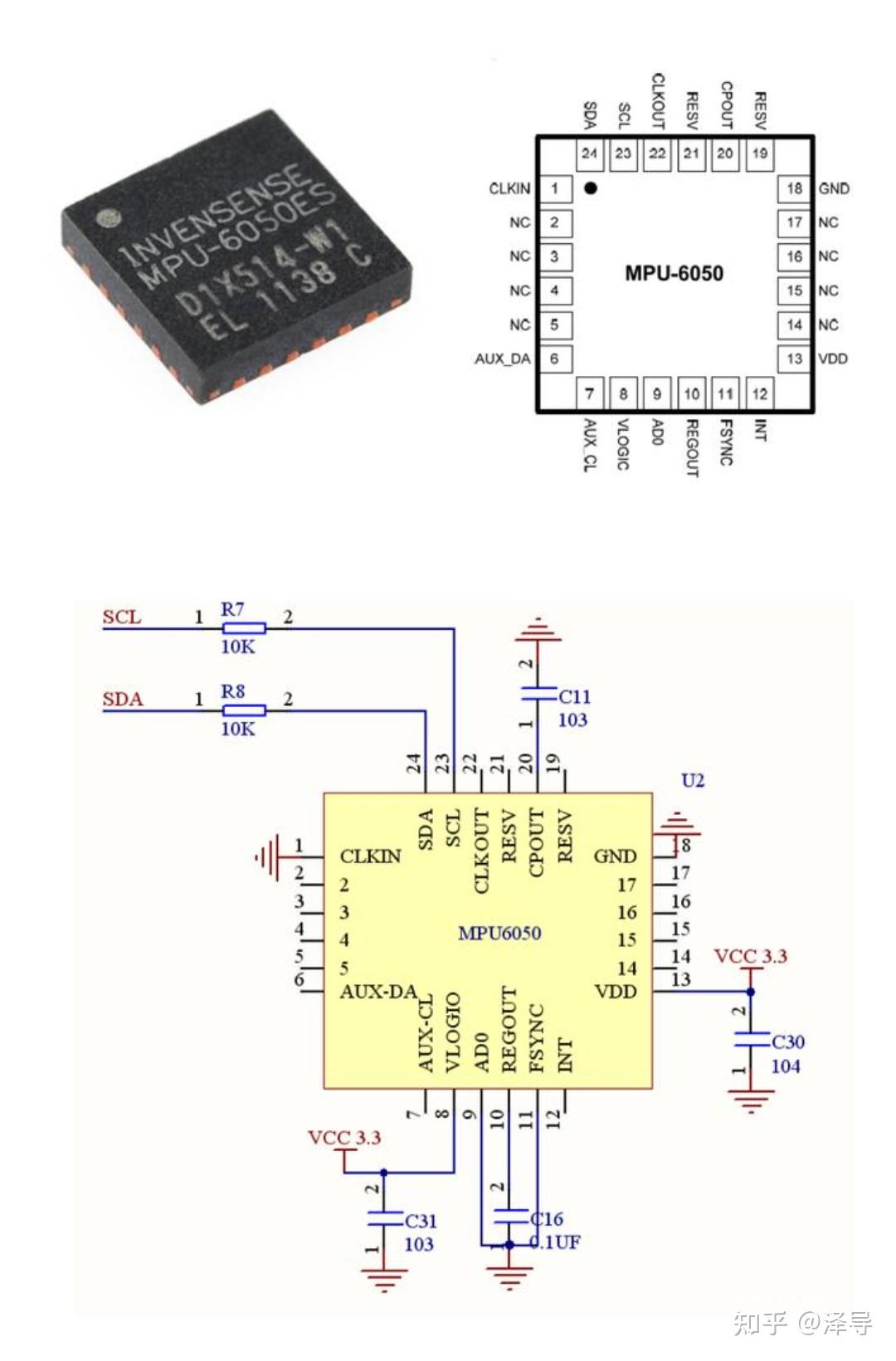

注：图片来源和没有详细推导的地方请查看对应的参考链接（呜呜呜嘿嘿嘿，神志不清+麻了.jpg）。

参考^https://baike.baidu.com/item/%E5%9B%9B%E5%85%83%E6%95%B0/5795379?fr=aladdin^https://zhuanlan.zhihu.com/p/45404840^https://www.zhihu.com/question/532400814/answer/2482525902^https://baike.baidu.com/item/%E6%AC%A7%E6%8B%89%E8%A7%92/1626212?fr=aladdin^https://zhuanlan.zhihu.com/p/45404840^https://www.zhihu.com/question/407150749/answer/1342043076^https://blog.csdn.net/lql0716/article/details/72597719^https://blog.csdn.net/qq_43460068/article/details/123490067^https://zhuanlan.zhihu.com/p/104820868^https://blog.csdn.net/AASDSADAD/article/details/73080832^https://baijiahao.baidu.com/s?id=1705722954735345671&wfr=spider&for=pc

【本文地址】

MPU

MPU

今日新闻

推荐新闻