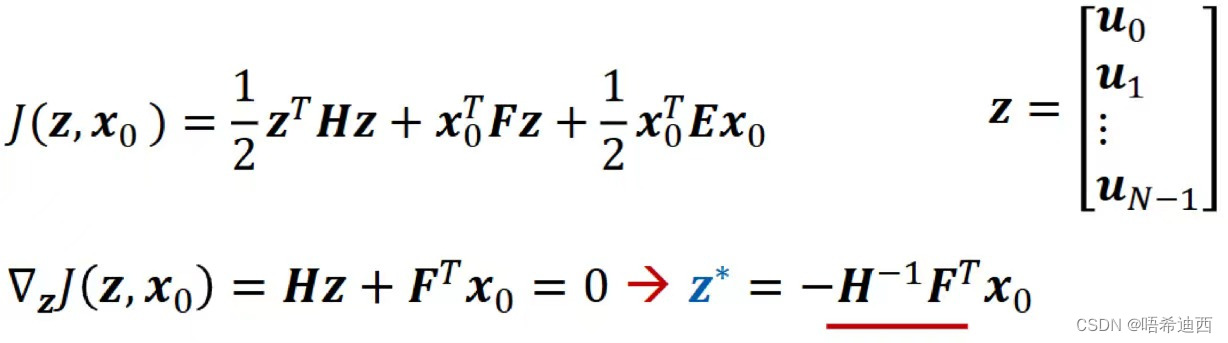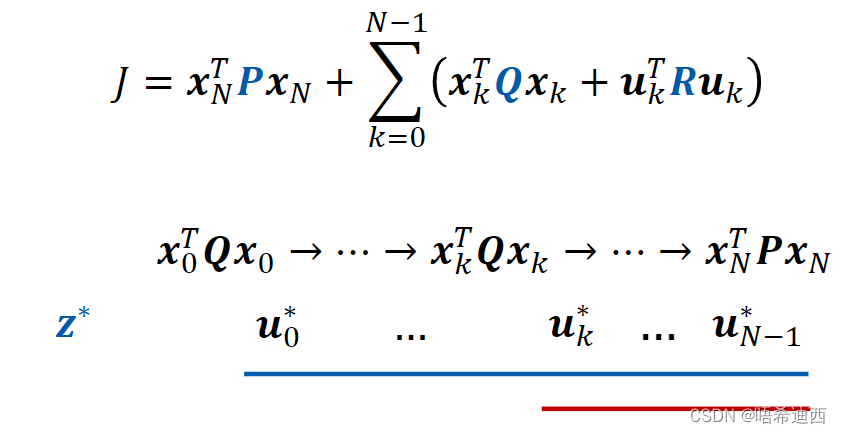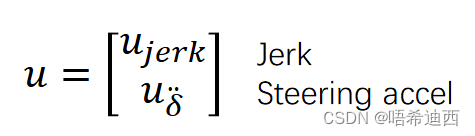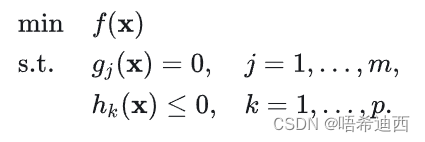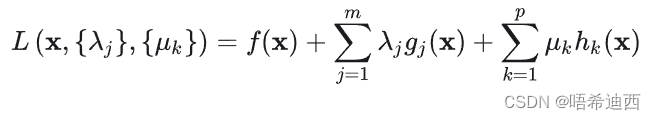第5章:模型预测控制(MPC) |
您所在的位置:网站首页 › mpc控制器的预测时域与采样时间 › 第5章:模型预测控制(MPC) |
第5章:模型预测控制(MPC)
|
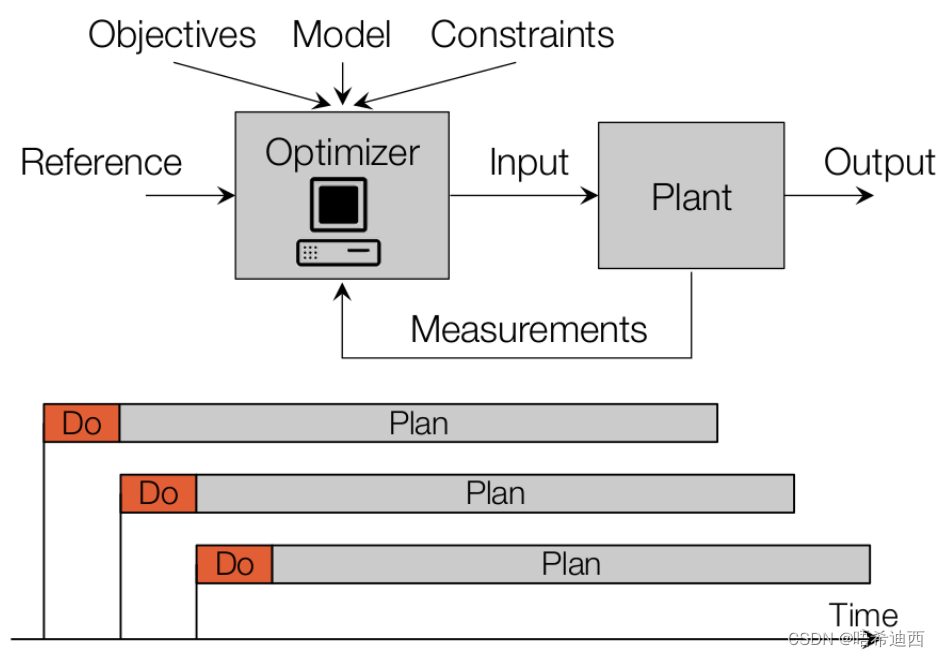
本文主要是介绍第5章:模型预测控制(MPC),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧! 5.1 模型预测控制(Model Predictive Controller -- MPC)注:MPC 更像是一种控制策略的框架,它使用了最优的控制思想在里面,如下的几种控制策略其实都是 MPC 的变体; MHC(Moving Horizon Control):滚动时域控制RHC(Receding Horizon Control):后退时域控制DMC(Dynamical Matrix Control):动态矩阵控制GPC(Generalized Predictive Control):广义预测控制 5.1.1 MPC 的基本原理
a 已知:系统的【误差型】【离散型】状态空间方程 a 注意: 如果在
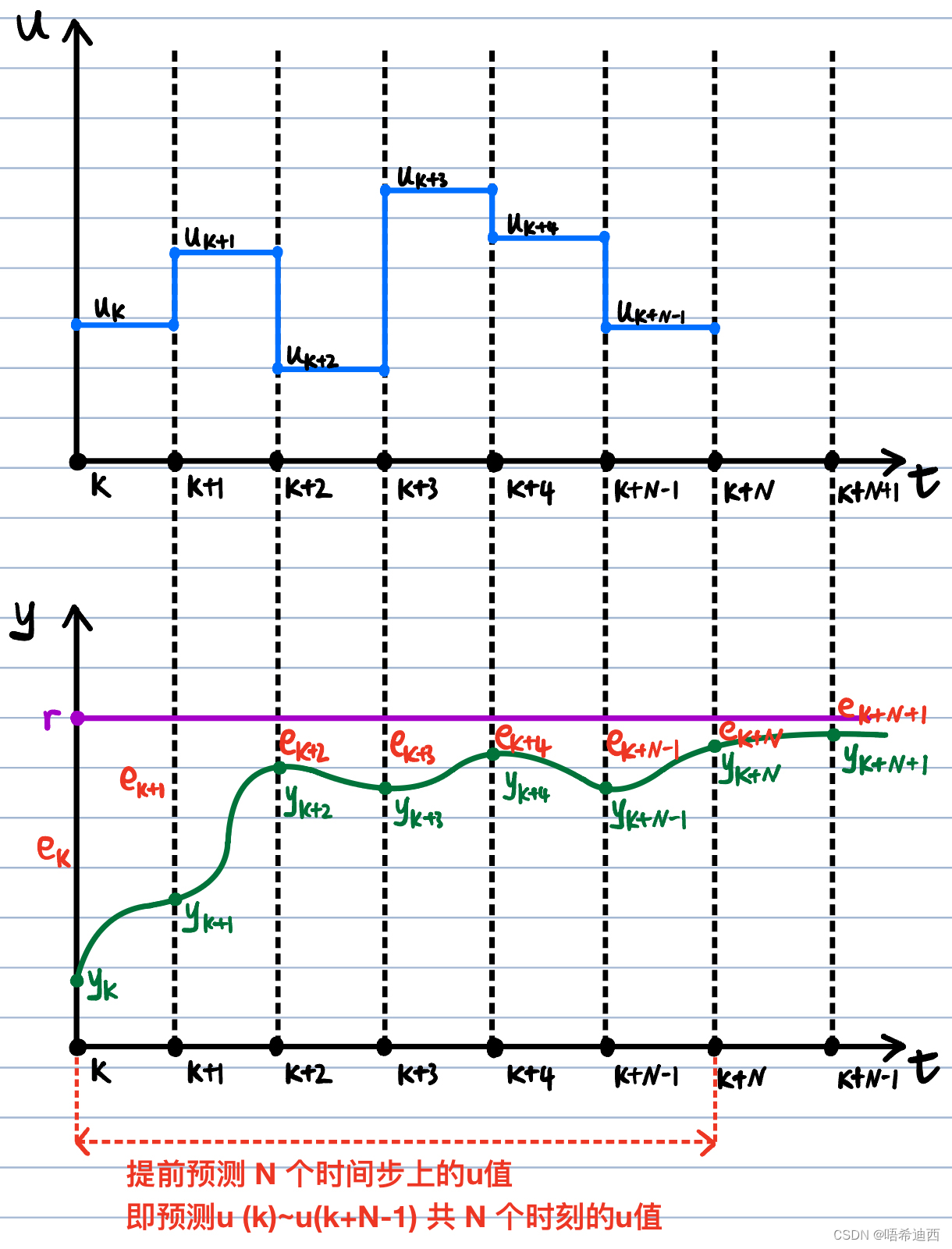
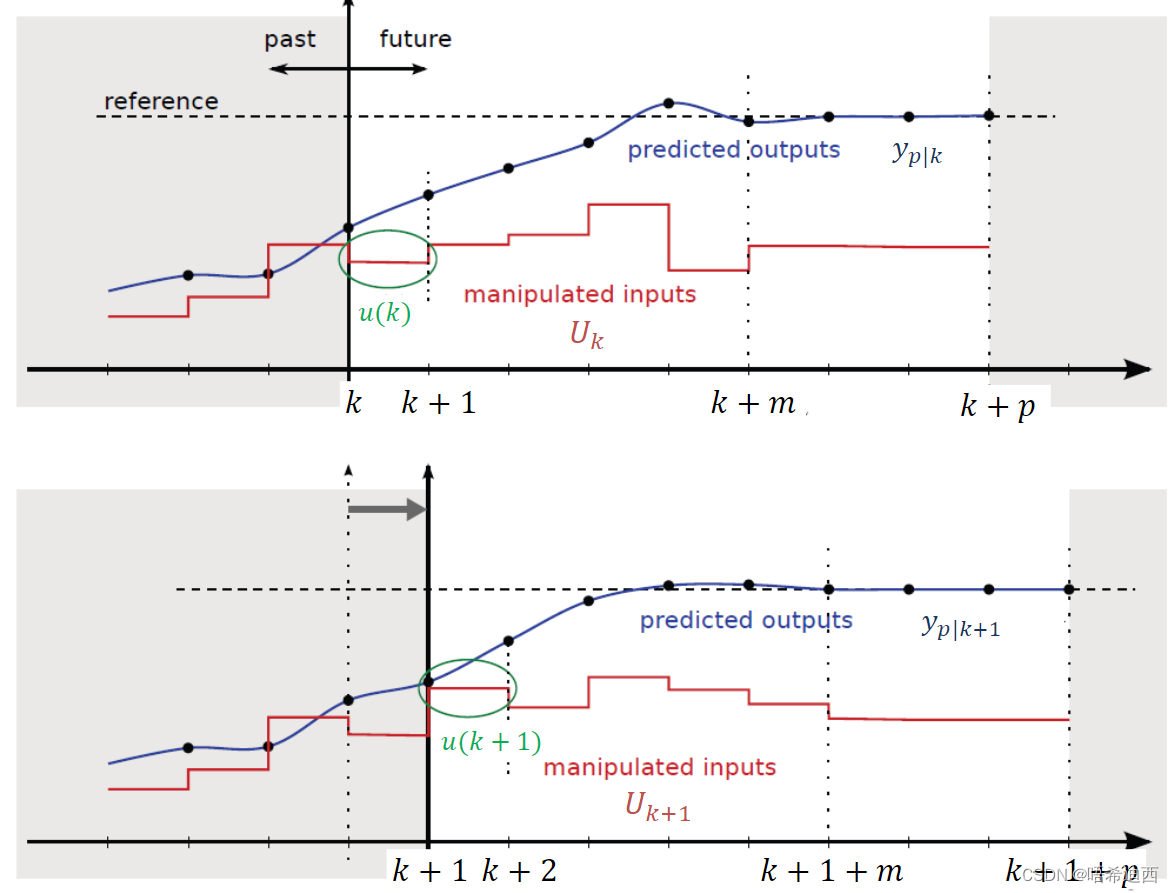
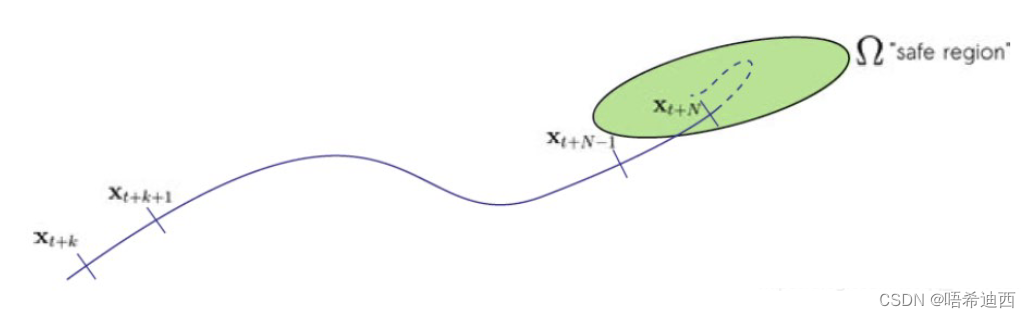
MPC 的设计理念: 假定当前系统处于时刻 k,则系统关于时刻 k 之前的所有信息都已知 已知MPC 控制器的基本原理: 直接在当前时刻 k 处预测出未来一个时间段内(假设含 N 个时间步,从时刻 k 到时刻 k+N-1)所有的控制动作总结:MPC 的工作流程 【1】在采样时刻 K 处获得当前的已知信息
注:无约束线性系统,是一定有解析解的; 无约束线性系统的模型预测控制: 线性:指系统的误差型离散型状态空间模型为线性的计算控制量 a Step1:建立代价函数 J
a a Step2:求解可以使得代价函数 J 的值最小的控制量 z
我们发现,针对线性无约束的系统使用 MPC 控制器,该系统的最优控制策略是线性的 计算控制量 问题: 我们已经得到直接计算控制量解决方案:使用动态规划(DP)的方法求解向量 z 的值 a a Step0:动态规划的理论基础是最优性原理 介绍:最优性原理是 bellman 等人提出的理论,可以将一个多阶段决策问题,变成一系列相互联系的单阶段问题,然后一个个解决;最优性原理:不管系统的初始状态 / 初始策略是什么,余下的控制策略一定符合最优控制策略;解释:就是说不管系统从哪一点出发,他的最优的控制策略最后一定会趋同;举例:比如我们现在的目的是从时刻 0 开始(系统初始状态为a a Step1:使用最优性原理将求解最优控制量
也就是说无论前面的 0 ~ k-1 步是如何达到时刻 k 时的状态 a a Step2:使用动态规划求解向量 z 的值
注意1:对于方法2,可以很明显看出 LQR 其实是线性无约束 MPC 的一种特殊情况 都是通过调用里卡提方程求解矩阵 Pa 解释: 线性无约束 MPC 求解的代价函数为:注意2:LQR 控制器与 MPC 控制器之间的区别 线性系统: LQR 控制器只能针对线性系统进行调节;MPC 不仅可以对线性系统进行调节,还可以对非线性系统进行调节;(只是这一节讲的就是线性无约束 MPC,并没有体现这个区别)约束条件: LQR 控制器不能对带有约束条件的系统进行控制;MPC 不仅可以对不含约束条件的系统进行控制,也可以对带有约束条件的系统进行控制;灵活性: LQR 只在当前时刻 k 处求出一个 P 矩阵,后面的控制策略全部使用这个 P 矩阵;MPC 的 P 矩阵在每个时间步都会重新求解,针对不同的情况进行相应的调整;是否在线: LQR 是离线控制策略,因为 P 矩阵是早已计算好的,所有时刻的控制策略都使用这同一个矩阵求解;MPC 是在线控制策略,在每个时间步处都要重新根据当前时刻的系统状态值,重新计算矩阵 P 的,所以他必须是在线的;注意3:通过上述两种方法,我们都可以得到一个结论,即针对线性无约束 MPC 控制器,控制策略为线性的( a 经典控制器(PID): 离线输出控制策略(不灵活):一直使用同一个控制策略,如MPC 控制器: 在线输出控制策略(灵活):控制策略随系统的变化而变化,如线性无约束 MPC,使用的控制策略a约束分为: 系统的状态空间方程:因为系统的状态空间方程就是车辆的动力学方程,车辆的行驶是一定要满足动力学方程的;物理约束:如电机转速最快是 1000,因此控制量不能是让电机转速达到 2000 转;安全约束:比如在一些环境中不允许变量调节超过这个环境所能承受的阈值(汽车在高速行驶时,若前轮转角大于某一阈值,会导致车辆侧翻),因此必须限制控制量的值;性能约束:我们对系统性能有一定的要求;a a MPC 控制器的缺点: 求解过于费时,对算力要求过高;a a 举例: 代价函数:不管是【线性系统有线性约束MPC】还是【线性系统有非线性约束MPC】,对问题的求解最重要的是我们如何将问题构造成一个二次型函数最优化的问题; 这样我们就可以通过调用现成的二次规划(QP)求解库进行求解; 常见的二次规划求解库: OOQPOSQPqpOASESECOS(SOCP)GUROBIMOSEK(LPs , QPs , SOCPs , MIPs ...)已知量: 系统的线性状态空间方程: 线性状态空间方程指的是,方程中涉及到的未知量a a 推导出: 二次型目标函数:(推导过程在上面)a (1)有线性约束线性系统的MPC求解过程: 将问题化为带线性约束的二次规划问题(凸优化问题)
常见的 QP 求解方法:
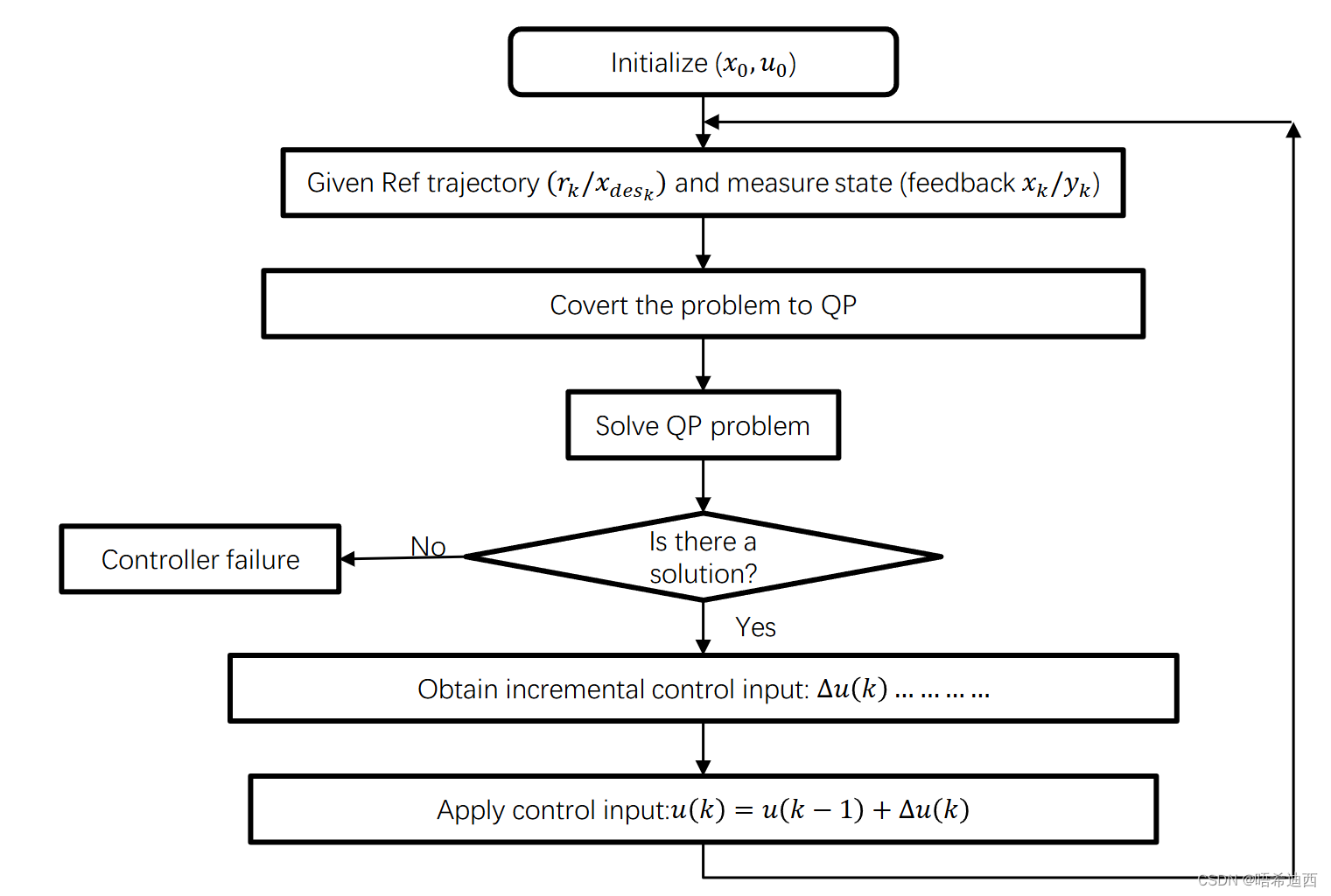
a (2)有非线性约束线性系统的MPC注:和上面的【有线性约束线性系统的MPC】的求解过程一模一样,只是其中的约束条件换成非线性的罢了;思路都是将原问题变成一个二次规划问题,再调用现成的二次规划求解库计算; 5.1.5 有约束非线性系统的MPC注:其实车辆并不是一个线性的系统,只是我们在推导车辆横向动力学模型的过程中,将系统中的非线性项(三角函数)全部使用假设化作了线性项(比如假设高速行驶条件,车辆转角很小,从而视 注:其实车辆是一个【有非线性约束的】【非线性的】系统 目标函数:求解过程: 已知带非线性约束的非线性系统构建模型,代价函数,约束条件调用市面上已有的成熟的求解库求解代价函数的极小值点注:市面上已有很多成熟的用来计算【非线性代价函数 + 非线性约束】问题的求解库,所以我们的主要任务就是如何针对带非线性约束的非线性系统 选取模型建立代价函数构建非线性约束条件给出合理的约束范围a a a a a a 5.2 使用 MPC 控制车辆的运动架构图:
注意:使用 MPC 控制器的系统架构和使用其他控制器(如 PID,LQR)的系统架构对比,可以发现多了一个【底层控制器(low level controller)】; 因为 PID / Stanely / LQR 这些控制器求解得到控制量的复杂度很低,也就是说求解控制量不会消耗很长的时间,因此通过控制器得到的控制量可以直接输出给车辆作为控制命令;但是 MPC 控制器的时间复杂度取决于对车辆系统的建模的复杂度,他每一轮都要求解 N 个未来时刻的动作,并且如果车辆的状态空间模型是非线性的话,二次规划的求解将更加难以收敛,更加缓慢,也就是说求解控制量会消耗很长的时间;所以可能出现这样的情况:时刻 k 时我们将反馈的状态量输给 MPC 控制器,但是 MPC 控制器计算出来时刻 k 应该采取的控制动作,需要三个时间步的时长,即一直到时刻 k+3 才能知道时刻 k 时应该采取什么动作,而我们必须在 k 时刻就知道应该采用什么样的控制动作;因此很难保证控制器输出控制信息的连续性和实时性,因此我们通过将 MPC 控制器视为上层控制器,再给系统加一个底层控制器,让 MPC 控制器还没有求解出来 k 时刻应该使用的控制量时,使用底层控制器(PID ... )代为操控,使得车辆的控制命令更为连续和高频,从而保证车辆的一个较好的抗干扰性能;a 使用 MPC 控制器的系统架构有以下几个重要的方面: 精确的车辆系统建模代价函数约束条件底层控制器 5.2.1 车辆运动模型构建 -- Curvilinear Coordinates Vehicle M注1:一个精准的模型可以使得在使用 MPC 求解最优控制量时更精确,但是也会耗费更长时间,所以在实际任务中,我们需要在【模型的简化】和【控制命令的准确度】之间进行一个权衡; 注2:主流使用的3种车辆模型 车辆横向运动学模型(Kinematic Bicycle Model) + 车辆纵向动力学模型车辆横向动力学模型(Dynamic Bicycle Model) + 车辆纵向动力学模型Curvilinear Coordinates Vehicle Modela (1)指定状态量 x 和输入量 u
取状态量 x 为:
取控制量 u 为:
a a 注意:控制量其实有多种选择,但是为什么选择第三种方式? 【速度a a 解释:选择第三种作为控制量有以下好处 微分没有积分精确; 如果我们得到的控制量是低阶的(如速度a (2)构建车辆模型 -- 推导过程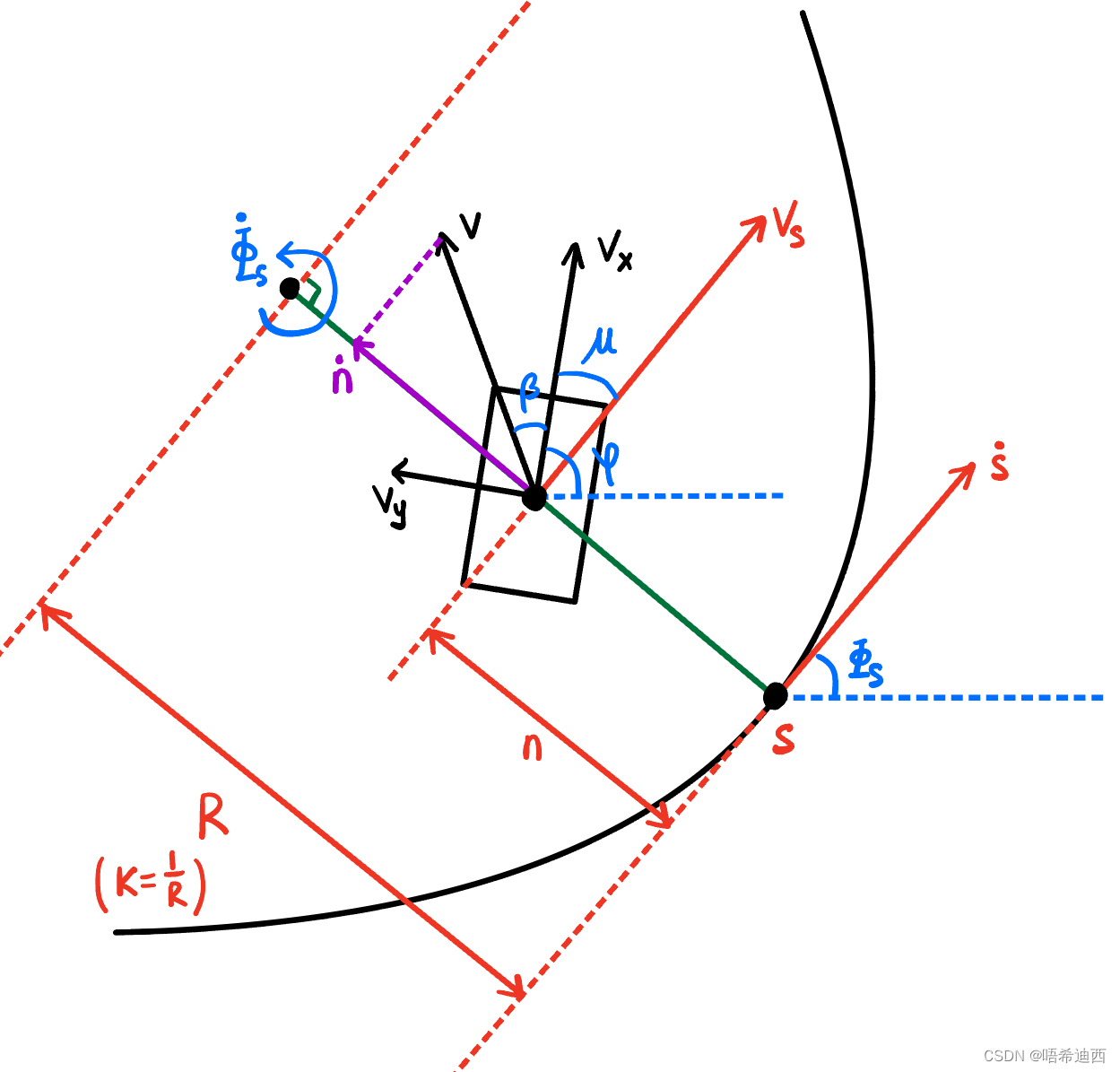 图1 图1 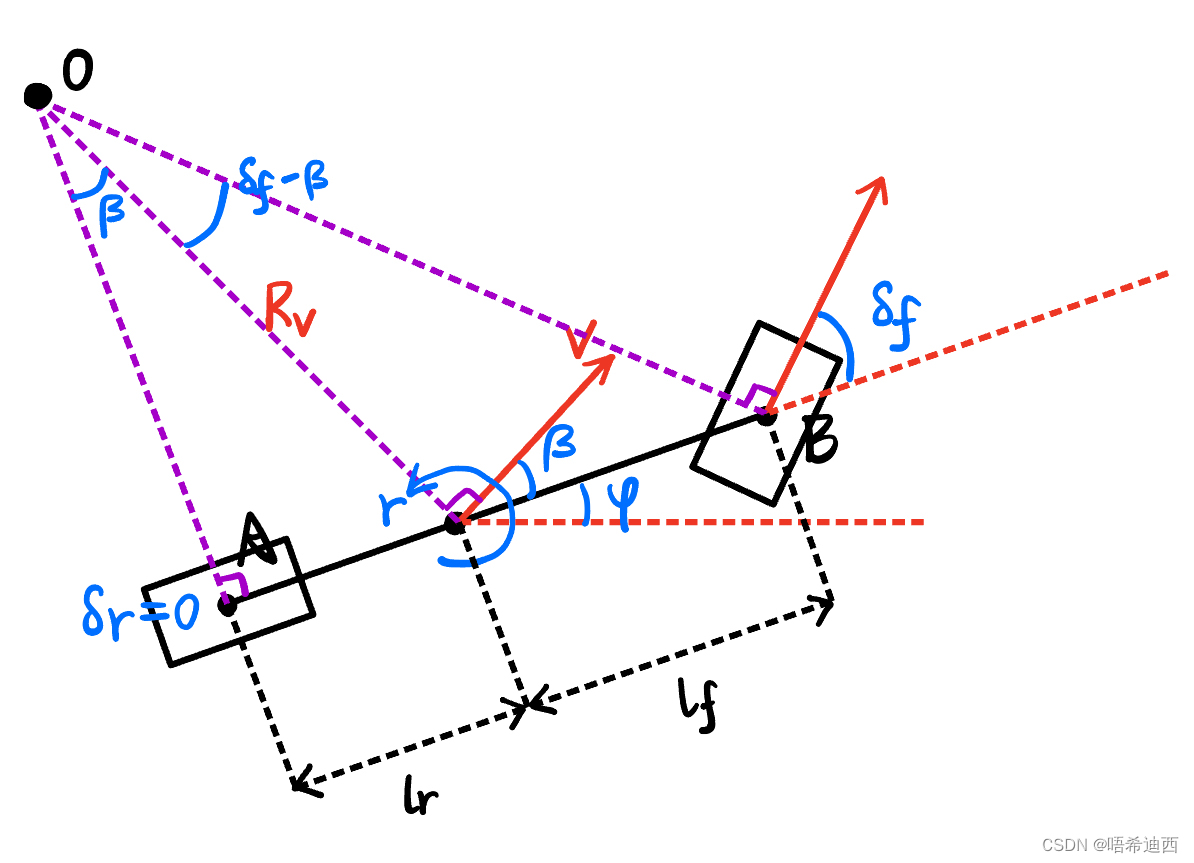 图2 图2
a a 注意:到目前为止上述公式中只有
总结:Curvilinear Coordinates Vehicle Model 模型特点 横纵向控制耦合在一起;包含了车辆的运动轨迹和参考线之间的相对位置关系;非线性(包含很多三角函数);注:正是由于 Curvilinear Coordinates Vehicle Model 模型是非线性的,并且耦合了横纵向控制,使得模型的精确性相对于之前使用的运动学模型 / 动力学模型有了很大的提升;但是随之,由于模型复杂度高了,对这个模型进行求解的速度会变慢;
代价函数分 4 部分: 跟踪参考轨迹的代价:a a a a (1)跟踪参考轨迹的代价a a (2)舒适性的代价a a (3)安全性的代价安全性代价设计思路: 控制器的上层,即规划器,他的主要任务就是根据周围的动态环境来建立一个安全可行范围,也就是说在这个范围内车辆的运动就是安全的,反之超出这个范围车辆的运动就是不安全的;这个安全行驶范围就是一个约束,所以我们可以按照车辆在实际行驶中对这个约束的违反程度来衡量系统的安全性;a 对车辆系统存在两种约束条件: 软约束(soft constraint):可以违反的约束就是软约束; 举例:车辆在某个车道内行驶过程时,是具有一个最优边界的,车辆在这个最优边界内行驶是最好的情况,但是超过也没事,我们的目的就是尽量让车在最优的区域内行驶,这就是软约束;硬约束(hard constraint):不能违反的约束就是硬约束; 举例:但是车辆在车道内的行驶绝对不能超出车道边界,这就是硬约束;注意:对于同一个物理量,它可以既有软约束,也可以有硬约束;对于一个物理量我们可以有一定的违反冗余度(软),但是这个违反的量不能超过一定的限制(硬);
a 如何在代价函数中表示软约束: 引入松弛变量(slack variables)a 引入了松弛因子这一新变量,原始最优化问题改变为:
注意:松弛变量 a a (4)代价函数无解 / 不收敛的代价MPC 控制器本身的限制 -- 两种情况: 第1种:代价函数在约束条件下无解,一般都是因为约束条件苛刻或者具有冲突;第2种:由于 MPC 控制器设定的有限时域长度 N 太小,导致虽然二次求解库可以求解当前代价函数 J 的极小值解,但是这 N 个时间步并不能使得车辆系统的状态量 x 收敛,及车辆系统无法到达稳定状态;a 解决思路: 对这 N 个步长的有限时域的终端状态
a 注意:代价函数本来是有 N 个 约束条件总结: 对状态量 x 和控制量 u 的约束:a (1)对目标点位置 s 的硬约束意义:在车辆行驶过程中,如果前方车辆插入我车目前行驶的车道,那么必须保证车辆当前所跟踪的目标点的 s 值不能超过前方障碍物车辆在我们的参考线上所匹配的参考点的 s 值;所以为了防止碰撞,这个约束必须为硬约束;
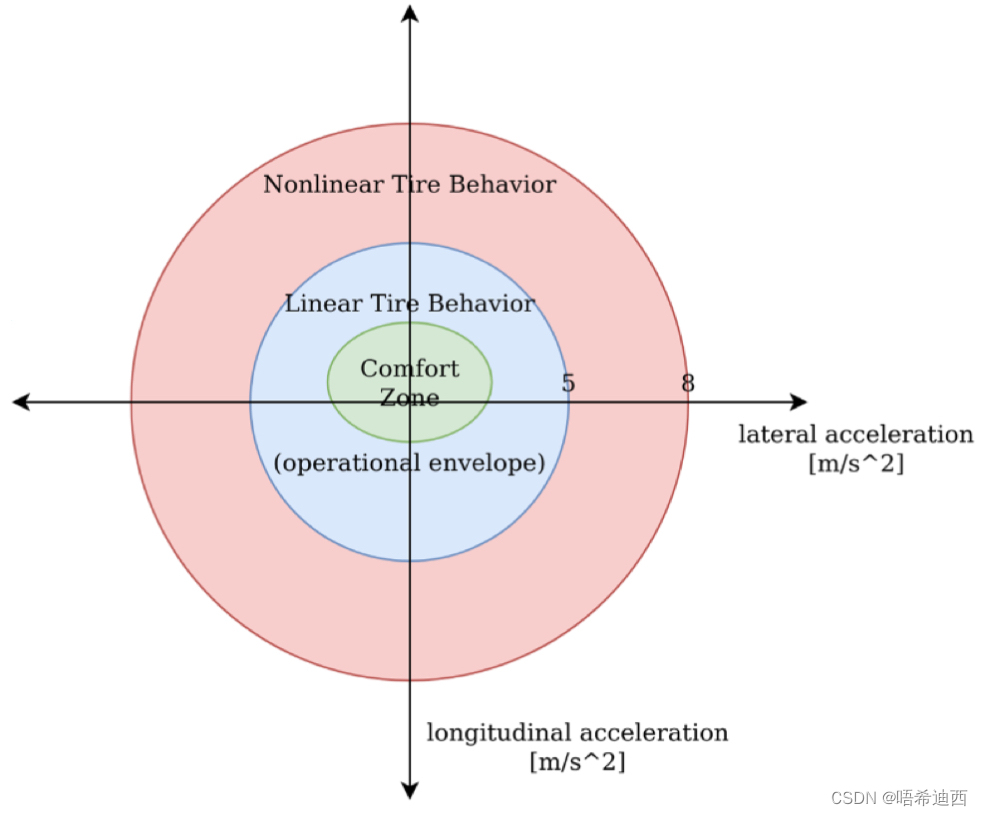
a 公式: 得到: a (2)对车辆速度 v 的软约束意义:对车辆的速度是一个软约束,因为很可能出现各种各样的情况导致车辆掉速,掉出当前时间步的理想速度范围 a 公式: 得到: a a (3)对车辆加速度 a 的硬约束和软约束注意:加速度 a 是横向加速度和纵向加速度耦合起来的总加速度; 硬约束意义:保证车辆的安全性; 在行驶过程中,如果纵向加速度很高,那么我们就要限制横向加速度的大小,否则横向加速度过大会导致车辆打滑;同理如果行驶时横向加速度很大,比如车辆在进行急转弯的时候,那么我们就要限制纵向加速度的大小,否则车辆会产生侧滑;一旦车辆发生了侧滑,对车辆的控制作用就会变得特别复杂,因为车辆轮胎的运动特征变成了非线性的;所以横向加速度和纵向加速度总是一大一小的;我们使用椭圆形的边界来约束横纵向加速度的大小;a a
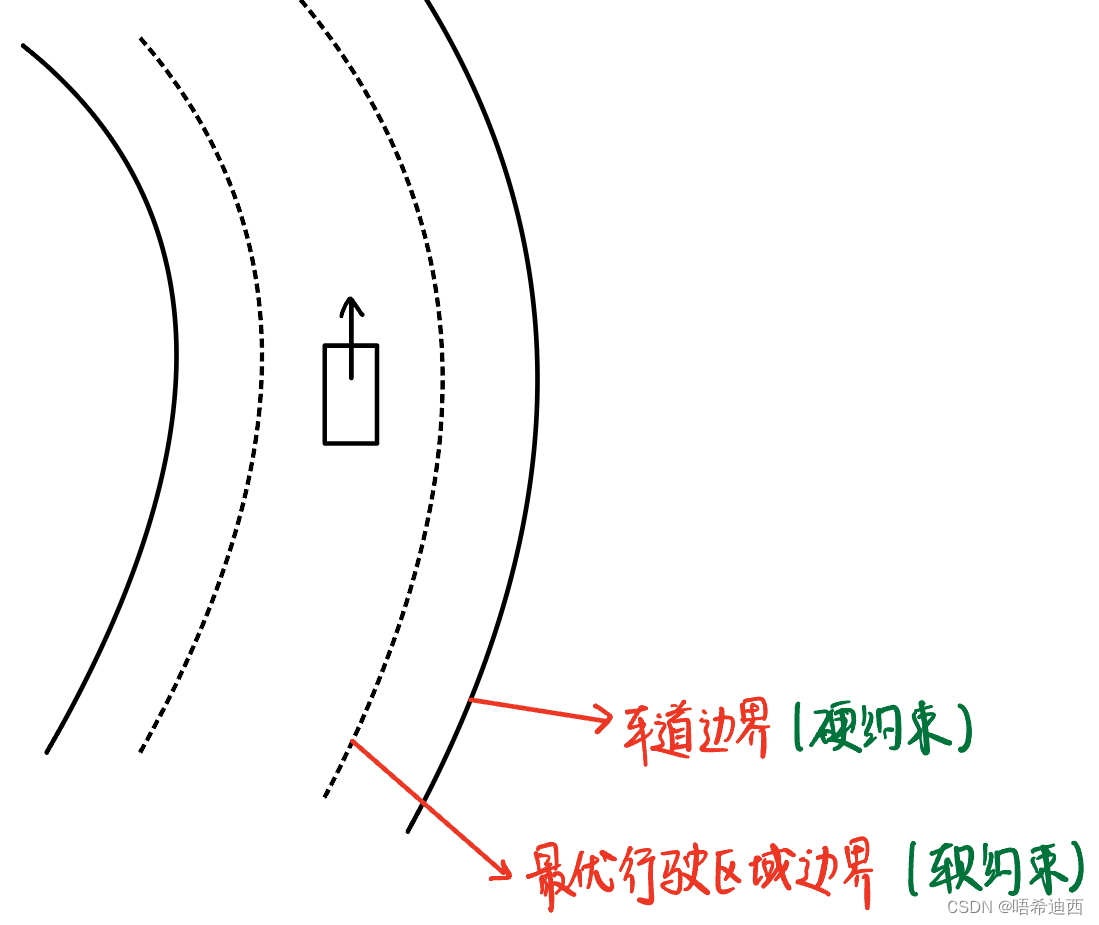
a a 公式: 得到: 软约束意义:保证车辆的舒适性; a 公式: 得到: a a (4)对车辆安全可行驶范围 tube 的硬约束和软约束
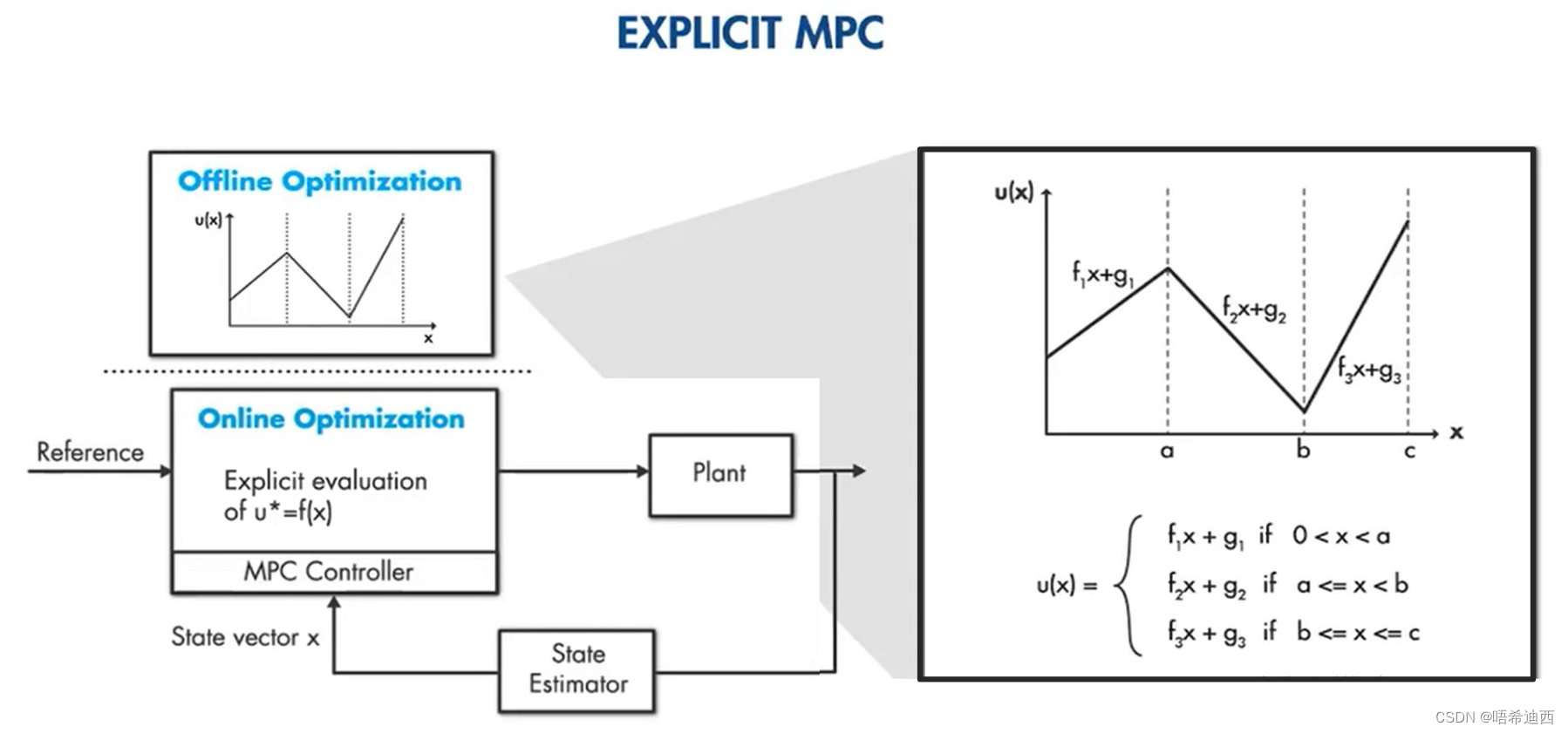
硬约束意义:防止车辆直接开出道路开到马路牙子上;软约束给出的范围是最优行驶空间,而硬约束给出的范围则是道路边界;下面的4个约束分别针对车辆的四个轮子,使四个轮子全都在马路牙子范围内运动; a 公式: a 得到: 软约束意义:令车辆在最优的安全行驶空间中运行; a a a a a a 5.3 总结已知: 车辆系统的非线性状态空间模型;代价函数;车辆系统的各种约束条件;a 得到:我们需要进行二次规划求解的问题 目标函数: a 限制条件: 状态空间方程:a a a a a a 5.4 主流二次规划求解器与 MPC 加速对于不同的系统,有不同的解法: Linear NonConstraint MPC:一定存在解析解,使用 DP 求解Linear / NonLinear Constraint MPC:使用 QP 求解 常用求解库(Linear):OSQP,qpOASES,FORCEs常用求解器(NonLinear):Codegen,acados 5.4.1 显性 MPC(Explicit MPC)求解 MPC 控制器的问题其实就是一个 QP 问题,但是 QP 问题的求解复杂度会随着【状态量 x 分量的个数】+【约束条件的个数】+【有限时域的长度】的增大而增大; 而在自动驾驶领域,我们要求控制器对车辆输出控制命令的频率要求很高,即车辆系统将状态量返回给控制器状态量的频率很高,对车辆系统状态量的采样时间间隔大概为几毫秒一次,因为要保证控制命令的实时性; 但是车载内存芯片大小有限,因此算力是有限的,如果 QP 问题过于复杂而且,而且每个几毫秒就要求解一次,那么 MPC 控制器这么大的计算量是不现实的;所以我们要减少 MPC 消耗的算力; 解决方法: 简化模型(减小模型阶数,简化模型参数)减小有限预测时域减少约束条件降低精确度要求Expilct MPCa a Expilcit MPC 的原理: 将一部分优化问题提前计算好,然后做成表存储起来,当 MPC 需要计算时,直接查找表里面的最优值即可;就是将 online 的问题变成了 offline 的问题; 具体实现: 制表(offline):按照初始状态离线求解方法:KKT 条件 Karush-Kuhn-Tucker (KKT)条件是非线性规划最佳解的必要条件文章链接:https://zhuanlan.zhihu.com/p/38163970a a 非线性规划问题:
定义 Lagrangian 函数:
4 个 KKT 条件:
a a 关于非线性规划的解的形式: 对于一个严格的多参数凸优化问题,他的解一定是连续的,解的形式一定是线性的;
这篇关于第5章:模型预测控制(MPC)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助! |
【本文地址】
今日新闻 |
推荐新闻 |