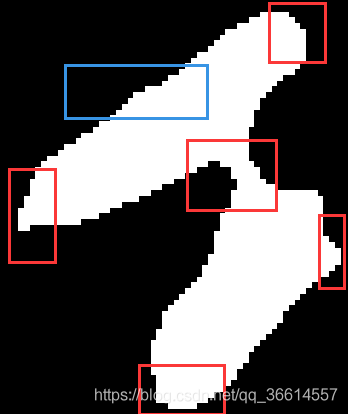
给定一个连通区域的图像，如下图所示，想要求其轮廓像素点的曲率。

理论上，下图红框中的轮廓像素的曲率应尽可能大，而蓝框的曲率应比较小。

 1.首先对图像二值化，并通过任意算子的边缘提取，得到初步的轮廓（白色像素点）：

2.但可能存在某处的轮廓的“厚度”大于1， 这样会影响之后按照顺序的轮廓点像素提取，所以对轮廓图像eg使用bwmorph进行细化：

得到细化后的轮廓：

3.细化后的轮廓，保证了某像素点的8邻域内，有且仅有两个其他轮廓点（一个是遍历的上一个像素点，一个是遍历的下一个像素点）。于是我们从任意一个轮廓点(sx,sy)出发， 沿着其8邻域内且未遍历过的像素点前进，直至回到起始点。除初始点外，其他点可供选择的邻域像素有且仅有一个，从而保证了程序能够正确地从初始点出发，遍历所有点后回到初始点。

因此我们定义矩阵x和y，用来存放按照顺序遍历的所有像素点的x坐标和y坐标，sx和sy为当前遍历点的坐标。dir为8邻域的方向，对于(sx,sy)的第i个邻域，其坐标为（sx+dir(i,1),sy+dir(i,2)）。定义一个函数findpoint，用来查找当前邻域像素点是否已经遍历过。如果邻域像素点值为1（白色），并且未遍历过，那么sx,xy更新为这个邻域像素点的坐标，并存入x,y。为了防止进入无限循环，设置了状态f，如果8个邻域像素都不能满足条件，说明走到了断头路，那么直接break。

函数findpoint，仅当sx和sy同时出现在x y的同一个索引下的值时，才返回0，表明该点已经遍历过，否则返回1.

4.这样得到的x和y连个矩阵（列表/向量），每个x(i),y(i)坐标的点，都会和x(i-1),y(i-1)以及x(i+1),y(i+1)相邻，因此用相邻的x(i)和x(i+1)的差值来近似在x方向的导数，y同理。因此得到一阶差值（导数）矩阵dfx1、dfy1；二阶差值（导数）在一阶差值（导数）基础上继续操作即可，得到dfx2,dfy2。

相邻差值可以用diff直接求得，但是会丢失最后一个点的差值，用x(1)-x(end)进行补充即可。

5.现在得到的差值矩阵dfx1(i),dfy(i)表示x(i)，y(i)点的“导数”，为了直观地显示图像中每个点的曲率，我们将dfx1等映射到二维矩阵dx1等，dfx1(i,j),dfy(i,j)表示点i,j的“导数”。

6.按照曲率公式进行计算曲率矩阵K：

为了防止分母为0，在分母加入0.1。

直接绘制K的图像：

颜色越白，代表曲率越大， 但是这样的结果很不满意，究其原因，是因为用离散点的差值来近似连续曲线的导数，误差太大（比如用(sin(1)-sin(0))/(1-0)近似sinx在x=0的导数，得到0.017，这和实际导数为1的误差过大）。因此，通过相邻差值的方法计算导数或者曲率效果并不好。

因此，我们试图去使用x(i+1)-x(i-1)代替x(i+1)-x(i)来近似x(i)，y(i)在x方向的导数：

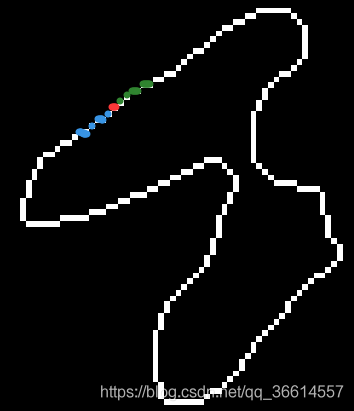
但是结果仍不可观，似乎准确地在离散的点中准确地近似导数是不太可能的事（或者尝试到附近n个点的差值？），特别是在特别小的图像而言。试想曲率的定义似乎和“直率”恰恰相反，也就是说这个像素点附近（这里指的是连续）的点呈现地越接近于直线，曲率越低，反而如果发生拐弯，曲率应该比较大，这不和线性回归有点像么！

因此，采用了线性回归的思路，对每个点的附近的点组成的线段的弯曲程度进行计算。假设取点x(i),y(i)之前共pre和点，之后共next个点，那么线段由pre+next+1个点组成，其坐标为x(i-pre:i+next),y(i-pre:i+next)。

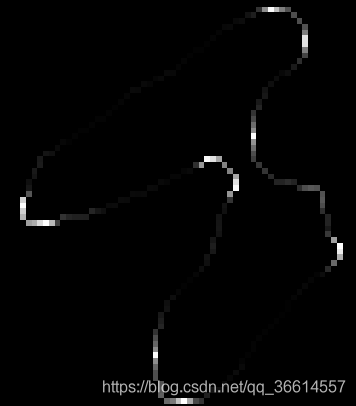
比如当前点用红色表示，之前的点用绿色表示，之后的点用蓝色表示，对他们进行线性回归后，所得的不呈直线的概率，或者回归的误差等参数都可以作为这个点的值。在此以regress返回的stats(1)为例，直线越直，这个stats(1)越接近于1，反之接近于0.因此在这用1-stats(1)表示弯曲程度。依次计算后得到的K为：

白色亮点分布在拐弯处，还是比较符合我们的要求的，OVER。

完整代码：

（为了避免讨论临界值问题，在线性回归时对x和y的边界进行了前后扩充）