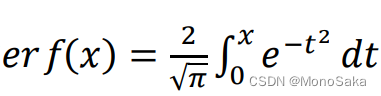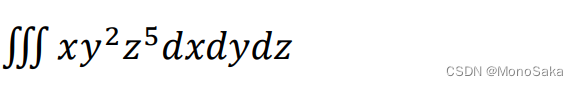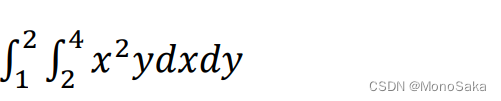【Matlab入门】 第五章 微分、积分运算和级数展开、求和 |
您所在的位置:网站首页 › matlab求积分代码 › 【Matlab入门】 第五章 微分、积分运算和级数展开、求和 |
【Matlab入门】 第五章 微分、积分运算和级数展开、求和
|
【Matlab入门】第五章 微分、积分运算和级数展开、求和
引言第五章 微分、积分运算和级数展开、求和一、微分运算1.极限运算Ⅰ 极限一般形式Ⅱ 单边极限形式
2.导数(微商)运算Ⅰ 一般求导(包括高阶导)Ⅱ 偏导数
3.常微分方程计算
二、积分计算1.不定积分的计算2.定积分、变上限积分的计算3.多重积分的计算4.数值积分的计算Ⅰ 梯形法Ⅱ 辛普森法Ⅲ 再多想一步
三、级数展开与级数求和1.级数展开Ⅰ 最基本展开Ⅱ 规定阶数Ⅲ 规定在哪展开
2.级数求和
本章更新记录
引言
首先很感谢各位的大力支持,能让本通识入门系列能出到第五章。 正如标题所见,本章主要讲述微分、积分运算和级数展开、级数求和。为何将这两个部分放在一起呢。因为考虑到matlab文章的受众大部分接受过高等教育。级数展开别名麦克劳林展开,这一部分在书本中和费马引理、罗尔中值定理和拉格朗日中值定理同时出现,是微分运算的重要理论体系。如此安排可以减小搜索和检索信息成本,一篇文章讲完,无需东拼西凑即可掌握如何使用matlab完成这些计算。 在进入本章学习之前,希望你有高等数学上册基础,且务必掌握第一章的内容。 第五章 微分、积分运算和级数展开、求和 一、微分运算 1.极限运算在极限运算中调用函数limit,具体用法如下: Ⅰ 极限一般形式一般形式就是类似于这样的: 调用limit求单边极限的方式和求一般极限的方式基本相似,只不过在末尾加入了“left”或者"right"选项。单边极限的数学形式如图,代码方式见代码块(以(x-3)/|x-3|在3处的左右极限为例): 导数的计算也很简单,调用的函数为diff。也分多种情况。 Ⅰ 一般求导(包括高阶导)一般求导的方式遵从数学中常见的求导准则。调用具体格式为:要求的导数 = diff (原函数体, 函数体内的符号变量, n) ,n为求导的阶数(求几次导数),当求一阶导时可省略,在这里以多项式3x^ 7+6x^ 3-2x^ 2为例,分别求1阶和2阶导: >> syms x; f = 3*x^7+6*x^3-2*x^2; >> A = diff(f,x) A = 21*x^6 + 18*x^2 - 4*x >> syms x; f = 3*x^7+6*x^3-2*x^2; >> B = diff(f,x,2) B = 126*x^5 + 36*x - 4思考 能实现这样的计算无疑对判断函数间断点或者极值有很大的意义。请你利用Ⅰ中多项式求导结果,在不动笔的前提下求出该函数的极值点和极值。再利用第三章中介绍的plot函数绘图验证。 思考完毕后再回到求导中来,在未指明阶数(譬如想要推n阶导时),matlab显得不那么愿意输出结果: >> syms x; f = 1/(x-2); %这里用了inf来表示无穷阶数下的导数 >> C = diff(f,x,inf) 错误使用 sym/diff Second and third argument must either be variables or a variable and a nonnegative integer specifying the number of differentiations. >> syms x n; f = 1/(x-2); %就算是我再定义变量,还是输不出表达式 >> C = diff(f,x,n) C = 0我在尽力解决这一问题,明天会加以补充,看文章的老爷们不要心急。 Ⅱ 偏导数对于多元函数的偏导数(定义为函数关于其中一个变量的导数而保持其他变量恒定(相对于全导数,在其中所有变量都允许变化)),自然会有不一样的求导结果,无非调用diff时加入嵌套,并且注意变量的位置。例如,我们要求 倘若还没学高数下,这一部分可以暂时先不了解。 3.常微分方程计算首先要介绍微分方程和导数的内置表达,csdn不便输入数学语言,所以请看下方图片: 我们发现在传统算法下,matlab报错了,翻译过来就是,字符串形式的实参将来不受支持。所以我们需要自动调用上一章介绍的sumfun函数,让函数体本身也是符号形式,且对cond部分也用变量代替,彻底杜绝字符串,就不会报错了: >> syms y(x); >> eqn = (diff(y,x)+a*y(x)+x==0);%用diff来代表y'这个一阶导,原本的dy已经不可用 >> cond = (y(0) == 1); >>> Sol=dsolve(eqn,cond) Sol = (exp(-a*x)*(a^2 - 1) + 1)/a^2 - x/a 二、积分计算 1.不定积分的计算在不定积分运算中,调用函数 int。其函数格式为:F=int(f, x)。其中,F 为积分出来的原函数,若被积函数 f 中只有一个变量,则 x 可省略。有趣的是,在生成原函数的时候,matlab不会补齐常数项,譬如我对1/(1+x^2)求积分: >> syms x; A = int(1/(1+x^2)) A = atan(x)正如第一章所说,matlab中的反三角函数只有a前缀,并不是arc。 2.定积分、变上限积分的计算在定积分运算中,仍要调用函数 int,函数格式为:F=int(f, x, a, b)。其中,a 和 b 分别为积分的下限和上限(千万不要混)。在求解无穷积分时,允许将 a、b 设定为–inf 或 inf(负无穷和正无穷)。若定积分得出的结果不是确切的数值,还可以 vpa()函数求出定积分的解,vpa函数用法很多,在此不展开叙述,学会使用这一种即可,以x^2 * cosx在-6到6的定积分和e ^(-x ^2)sinx在0到inf的变上限积分为例: >>%定积分例 >> syms x; F=int(x^2*cos(x), -6, 6) F = 24*cos(6) + 68*sin(6) >> vpa(F) ans = 4.0438330020818251419098847805413 >>%变上限积分例 >> syms x; F=int(exp(-x^2)*sin(x), 0, inf) F = -(pi^(1/2)*erf(1i/2)*exp(-1/4)*1i)/2 >> vpa(F) ans = 0.42443638350202229593404235248967新出现的erf又是什么鬼?它也是函数,但是在统计中使用居多,尤其是正态分布,给它的伪装卸下来,你就豁然开朗了(高中学过,如果不开朗也没关系,下章预告:统计和拟合): 多重积分的计算由嵌套int来实现,并没有什么特别的,有几重就套几重,以一个三重不定积分为例: 有不定就有定,一样的道理,以一个二重定积分为例: 数值积分,用于求定积分的近似值。在数值分析中,数值积分是计算定积分数值的方法和理论。在数学分析中,给定函数的定积分的计算不总是可行的。许多定积分不能用已知的积分公式得到精确值。譬如高等数学教材明确表示过sinx/x的不定积分无法直接求出,此时用这种近似逼近的方法求对应的定积分非常合适。 >> syms x;int(sin(x)/x) ans = sinint(x) %你看,连它自己都开始糊弄人了 >> syms x ;f = sin(x)/x;F = int(f,0,1/8) F = sinint(1/8) %依旧是糊弄人数值逼近有多种算法,常见的是梯形法和辛普森法。 Ⅰ 梯形法使用梯形法近似计算定积分的函数格式为:F=trapz(x, y)。其中,x 可以为行向量或者列向量,y 的行数应该等于 x 向量的元素数。该函数需要在 x 和 y 建立起向量,即对积分空间[a,b]进行分割的基础上执行。梯形法的具体原理让我们看看官方文档: 有人可能要问了,为什么不用符号变量,因为这是求取定积分,我们需要对x的范围做限制,且作为估计的逼近方式,使用linspace生成向量的不连续度并不会对结果产生太大影响,我们现在就对下面这个式子做梯形法估计: 使用辛普森方法近似计算定积分的函数格式为:F=intergral(f, a, b)。其中,f 用于描述被积函数,需要注意的是,这里的f需要为函数句柄,如何理解?对于初学者而言先不必了解,知道其格式为f = @(自变量) 函数 即可。a和 b分别为积分上限和下限。(如果你的版本真的很老,甚至早于2016a,调用函数为quad)。 intergral函数用法非常杂,在此仅介绍如何用它来逼近定积分,还是用上面那个例子: >> f=@(x) exp(-2*x); F = integral(f, 0, 1/8) F = 0.1106可以看到二者逼近的值一模一样,那是否和真实值一样呢? >> syms x;f=exp(-2*x);F = int(f,0,1/8) F = 1/2 - exp(-1/4)/2 >> vpa(F) ans = 0.11059960846429756587741486651084误差很小,可以拿来放心使用。 Ⅲ 再多想一步使用梯形方法对定积分的值进行逼近时,我们是用linspace来定义x的,倘若我们再缩小步距,让梯形更密集,让梯形的斜边更加拟合曲线,能得到更加准确的值吗? >> x=linspace(0,1/8,100); y=exp(-2*x); F2=trapz(x,y) F2 = 0.1106为什么没有更加精确呢,并不是咱们想的有问题,而是matlab显示小数点后几位数的问题。现在点击最上方窗口第五部分的预设-命令行窗口-文本显示-数值格式-从short换成long,这下试试,就截然不同了: >> x=linspace(0,1/8,10); y=exp(-2*x); F2=trapz(x,y) F2 = 0.110606719973182 >> x=linspace(0,1/8,100); y=exp(-2*x); F2=trapz(x,y) F2 = 0.110599667237848步距大时和精确值相差-7.052735334134308e-06,步距变小时和精确值相差-1.665334536937735e-16。精确度完全不在一个数量级上。可见减小步距对精度影响虽然微小,但也是有的。 三、级数展开与级数求和 1.级数展开泰勒展开,麦克劳林展开式的高等数学内容,详见本站文章【浅谈泰勒公式与麦克劳林公式】https://blog.csdn.net/tonglin12138/article/details/106038316 Ⅰ 最基本展开本部分主要讲如何用函数快速生成麦克劳林展开式,以sinx为例,直接调用taylor函数: >> syms x;taylor(sin(x)) ans = x^5/120 - x^3/6 + x %这是5阶的展开式 Ⅱ 规定阶数我们也可以规定展开几阶。补充order选项即可。但是要注意,你想要的阶数永远比你输入的数字小1。 >> >> syms x;taylor(sin(x),'order',4) ans = - x^3/6 + x Ⅲ 规定在哪展开我们还可以规定在哪个点展开,补充ExpansionPoint选项即可,第三点和第二点可以混合使用,譬如,让自然指数在x = 2处展开,并且要求7阶。看图即可掌握格式: >> syms x;taylor(exp(x),'ExpansionPoint',2,'order',8) ans = exp(2) + exp(2)*(x - 2) + (exp(2)*(x - 2)^2)/2 + (exp(2)*(x - 2)^3)/6 + (exp(2)*(x - 2)^4)/24 + (exp(2)*(x - 2)^5)/120 + (exp(2)*(x - 2)^6)/720 + (exp(2)*(x - 2)^7)/5040 2.级数求和级数求和部分待补充,鄙人欠缺较多知识点。明日学完再来补充。 本章到此结束。如有问题,请及时联系我。 本章更新记录2024.2.17首次发布。 2024.2.18修改了一处排版错误。 |
【本文地址】
今日新闻 |
推荐新闻 |
 调用limit函数求一般形式极限的格式为:任意变量 = limiit(函数体,函数内的符号变量,逼近的值),以对sinx/x求极限为例,代码块如图:
调用limit函数求一般形式极限的格式为:任意变量 = limiit(函数体,函数内的符号变量,逼近的值),以对sinx/x求极限为例,代码块如图:
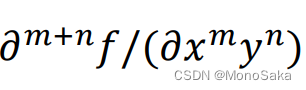 类似于这种形式的关于多元函数f(x,y)的偏导数,格式为变量=diff(diff (f, x, m), y, n) 或者 变量=diff(diff (f, y, n), x, m)。接下来引一道例题,f(x, y, z) = sin((x^ 2)y)e ^((-x ^2)y-z ^2),求偏导(格式如下方所示):
类似于这种形式的关于多元函数f(x,y)的偏导数,格式为变量=diff(diff (f, x, m), y, n) 或者 变量=diff(diff (f, y, n), x, m)。接下来引一道例题,f(x, y, z) = sin((x^ 2)y)e ^((-x ^2)y-z ^2),求偏导(格式如下方所示): 
 在指明自变量的情况下,函数格式为:r = dsolve(‘eq1’, ‘eq2’,┄, ‘cond1’, ‘cond2’,┄, ‘x’)。其中,eq1,eq2,┄为指定的常微分方程的符号解。常微分方程以变量 x 为自变量,参数’cond1’,‘cond2’,┄用于指定方程的边界条件或者初始条件。符号解如何理解呢,对于没学过线性代数或者这一部分的人来说可能比较陌生,其实算是这个方程的“通解”,当有cond输入时,通解才能成为唯一解,所以这些变量的输入都是必不可少的。 但是警告!!!!!!!!这种调用法在2022a版本中已经不可用,具体的计算方式请再往下看一看!!! 之所以要贴出错误用法,就是让各位加深记忆,同时明白软件更迭了什么。 以Dy + a*y + x = 0 y(0) = 1为例展示dsolve函数的错误用法:
在指明自变量的情况下,函数格式为:r = dsolve(‘eq1’, ‘eq2’,┄, ‘cond1’, ‘cond2’,┄, ‘x’)。其中,eq1,eq2,┄为指定的常微分方程的符号解。常微分方程以变量 x 为自变量,参数’cond1’,‘cond2’,┄用于指定方程的边界条件或者初始条件。符号解如何理解呢,对于没学过线性代数或者这一部分的人来说可能比较陌生,其实算是这个方程的“通解”,当有cond输入时,通解才能成为唯一解,所以这些变量的输入都是必不可少的。 但是警告!!!!!!!!这种调用法在2022a版本中已经不可用,具体的计算方式请再往下看一看!!! 之所以要贴出错误用法,就是让各位加深记忆,同时明白软件更迭了什么。 以Dy + a*y + x = 0 y(0) = 1为例展示dsolve函数的错误用法: