【Matlab】求解微分方程{上}(通解和特解) |
您所在的位置：网站首页 › matlab方程组绘图 › 【Matlab】求解微分方程{上}(通解和特解) |
【Matlab】求解微分方程{上}(通解和特解)
|
求解微分方程
desolve函数实例1实例2实例3实例4
求解有条件的微分方程微分方程显示隐式解未找到显式解决方案时查找隐式解决方案求微分方程级数解为具有不同单边限制的函数指定初始条件（特解）练习题
desolve函数
S = dsolve(eqn)求解微分方程eqn，其中eqn是符号方程。使用diff和==来表示微分方程。例如，diff(y,x) == y表示方程dy / dx = y。通过指定 eqn为这些方程的向量来求解微分方程组。
S = dsolve(eqn,cond)eqn用初始或边界条件求解cond。
S = dsolve(___,Name,Value) 使用由一个或多个Name,Value对参数指定的附加选项。
[y1,...,yN] = dsolve(___)将解分配给变量y1,...,yN。
求解y关于什么的函数就要声明为y (x) ，必须使用syms来声变量, 否则会被警告 实例1d d x y ( t ) = − 3 y ( t ) \frac{d}{{dx}}\operatorname{y} \left( t \right) = - 3\operatorname{y} \left( t \right) dxdy(t)=−3y(t) %案例一 clear all clc syms y(t); eqn=diff(y,t) == -3*y F=dsolve(eqn) latex(F)
结果和上面相似 实例3d d x y ( t ) = 3 x 2 \frac{d}{{dx}}\operatorname{y} \left( t \right) = 3{x^2} dxdy(t)=3x2 %案例三 clear all clc syms y(t) x eqn=diff(y,t)==3*x^2 F=dsolve(eqn) latex(F)
d 2 d x 2 y ( t ) = a y ( t ) \frac{{{d^2}}}{{d{x^2}}}\operatorname{y} \left( t \right) = a\operatorname{y} \left( t \right) dx2d2y(t)=ay(t) %二阶案例一 clear all clc syms y(t) a eqn = diff(y,t,2) == a*y ySol(t) = dsolve(eqn) latex(ySol(t))
d y d t = z d z d t = − y \begin{gathered} \frac{{dy}}{{dt}} = z \\ \frac{{dz}}{{dt}} = - y \\ \end{gathered} dtdy=zdtdz=−y %有条件的微分方程 clear all clc syms y(t) z(t) eqns = [diff(y,t) == z, diff(z,t) == -y] S = dsolve(eqns)dsolve返回一个包含解的结构
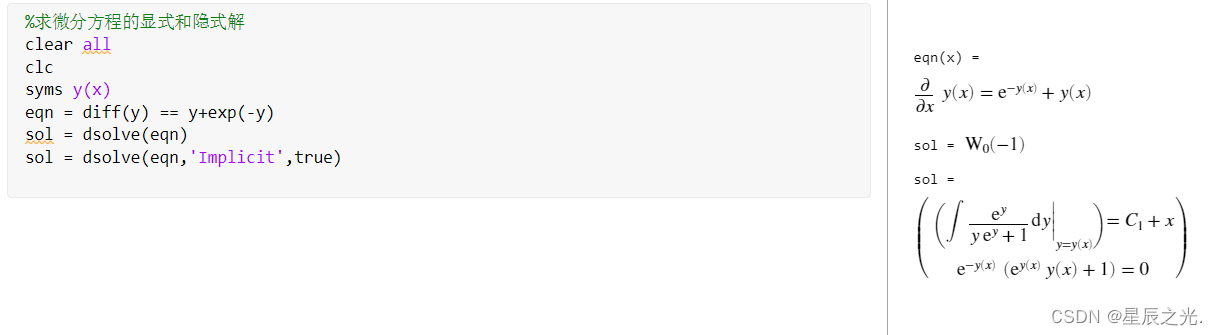
∂ ∂ x y ( x ) = e − y ( x ) + y ( x ) \frac{\partial }{{\partial x}}\operatorname{y} \left( x \right) = {e^{ - \operatorname{y} \left( x \right)}} + \operatorname{y} \left( x \right) ∂x∂y(x)=e−y(x)+y(x) %这里我们设置"Inplicit"为True sol = dsolve(eqn,'Implicit',true) %求微分方程的显式和隐式解 clear all clc syms y(x) eqn = diff(y) == y+exp(-y) sol = dsolve(eqn) sol = dsolve(eqn,'Implicit',true)
∂ ∂ t y ( x ) = y ( x ) + a y ( x ) \frac{\partial }{{\partial t}}\operatorname{y} \left( x \right) = \operatorname{y} \left( x \right) + \frac{a}{{\sqrt {\operatorname{y} \left( x \right)} }} ∂t∂y(x)=y(x)+y(x) a 同时我们已知 y ( a ) = 1 y(a)=1 y(a)=1 %当未找到显式解决方案时查找隐式解决方案 clear all clc syms a y(t) eqn = diff(y,t) == a/sqrt(y) + y cond = y(a) == 1; ySimplified = dsolve(eqn, cond)
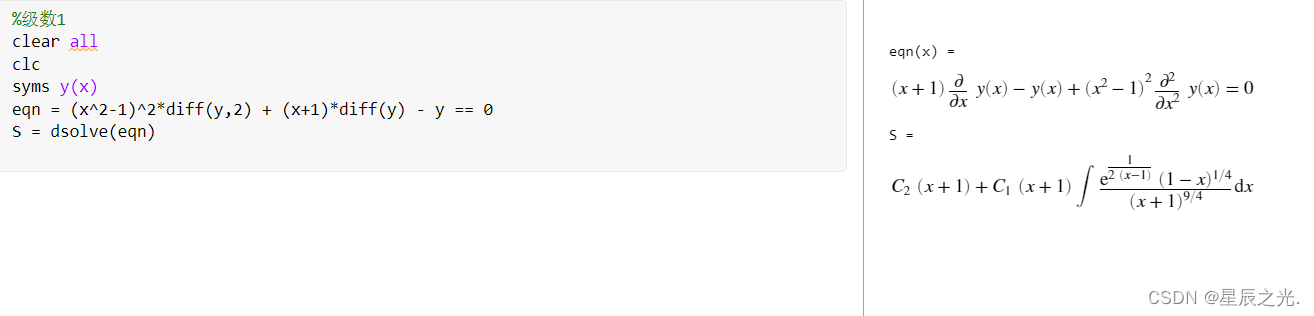
dsolve返回包含未计算积分项的解 ( x + 1 ) ∂ ∂ x y ( x ) − y ( x ) + ∂ 2 ∂ x 2 y ( x ) = 0 \left( {x + 1} \right)\frac{\partial }{{\partial x}}\operatorname{y} \left( x \right) - \operatorname{y} \left( x \right) + \frac{{{\partial ^2}}}{{\partial {x^2}}}\operatorname{y} \left( x \right) = 0 (x+1)∂x∂y(x)−y(x)+∂x2∂2y(x)=0 %级数1 clear all clc syms y(x) eqn = (x^2-1)^2*diff(y,2) + (x+1)*diff(y) - y == 0 S = dsolve(eqn)
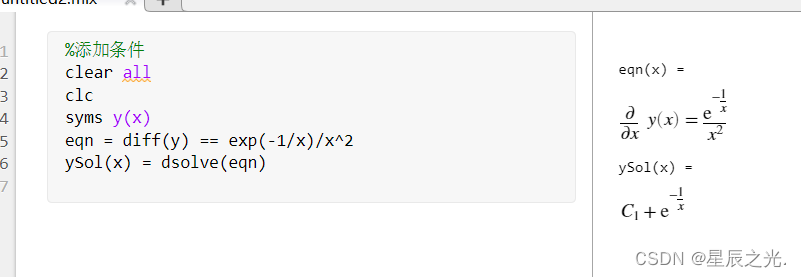
∂ ∂ x y ( x ) = e − 1 x x 2 \frac{\partial }{{\partial x}}\operatorname{y} \left( x \right) = \frac{{{e^{ - \frac{1}{x}}}}}{{{x^2}}} ∂x∂y(x)=x2e−x1 %添加条件 clear all clc syms y(x) eqn = diff(y) == exp(-1/x)/x^2 ySol(x) = dsolve(eqn)
可以直接敲代码试试
d
y
d
t
+
4
y
(
t
)
=
e
−
t
,
y
(
0
)
=
1
\frac{{dy}}{{dt}} + 4\operatorname{y} \left( t \right) = {e^{ - t}},y(0)=1
dtdy+4y(t)=e−t,y(0)=1 |
C
1
e
−
3
t
C_{1}\,{\mathrm{e}}^{-3\,t}
C1e−3t
3
t
x
2
+
C
1
3\,t\,x^2+C_{1}
3tx2+C1
C
1
e
−
a
t
+
C
2
e
a
t
C_{1}\,{\mathrm{e}}^{-\sqrt{a}\,t}+C_{2}\,{\mathrm{e}}^{\sqrt{a}\,t}
C1e−a
t+C2ea
t
C
1
cos
(
t
)
+
C
2
sin
(
t
)
C_{1}\,\cos\left(t\right)+C_{2}\,\sin\left(t\right)
C1cos(t)+C2sin(t)
C
2
cos
(
t
)
−
C
1
sin
(
t
)
C_{2}\,\cos\left(t\right)-C_{1}\,\sin\left(t\right)
C2cos(t)−C1sin(t)
(
∂
∂
t
y
(
t
)
=
4
z
(
t
)
∂
∂
t
z
(
t
)
=
−
3
y
(
t
)
)
\left( {\frac{\partial }{{\partial t}}\operatorname{y} \left( t \right) = 4\operatorname{z} \left( t \right)\,\frac{\partial }{{\partial t}}\operatorname{z} \left( t \right) = -3\operatorname{y} \left( t \right)} \right)
(∂t∂y(t)=4z(t)∂t∂z(t)=−3y(t))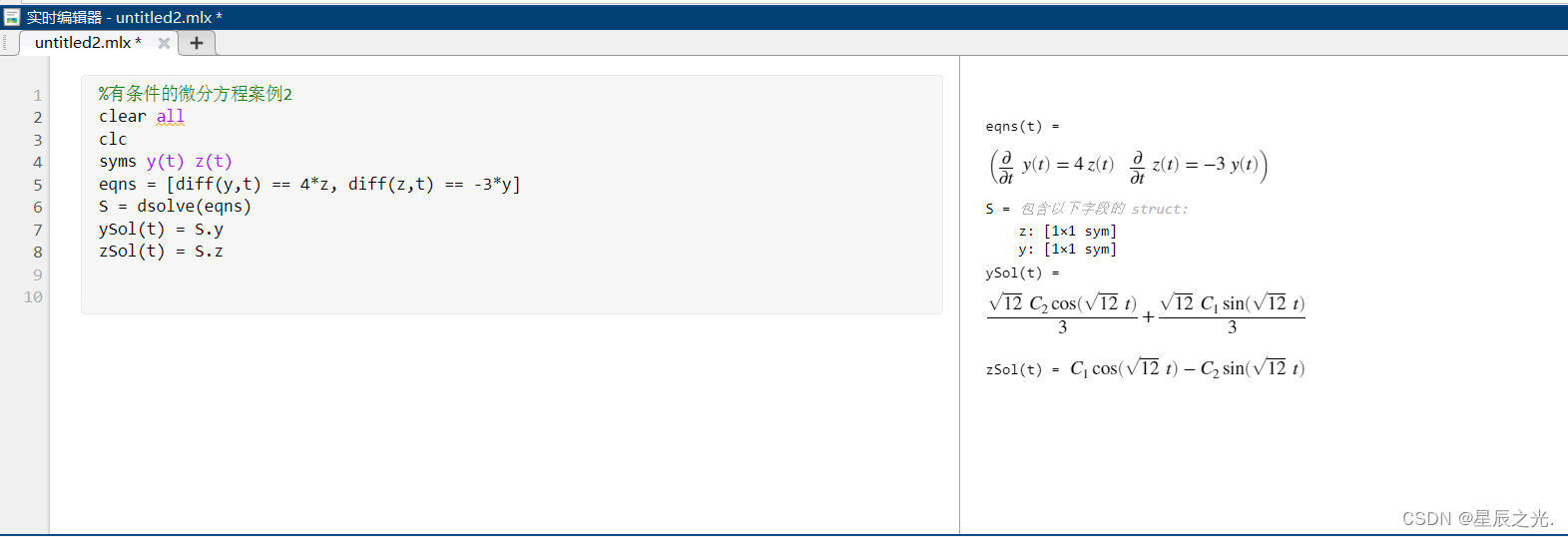
其实也可以直接用
若要返回包含参数a的所有可能值的解决方案，请通过将"lgnoreAnalyticConstraints"设置为false来关闭简化。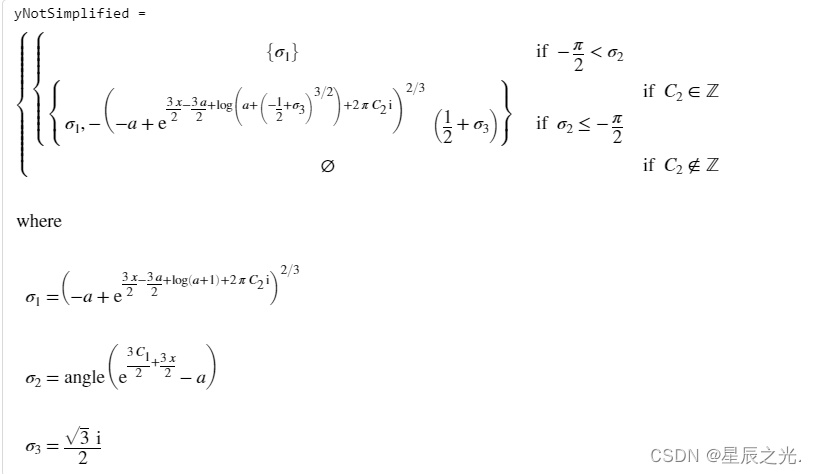
但是若要返回x=-1附近微分方程的级数解，请将“ExpansionPoint"设置为 -1。dsolve 根据Puiseux级数展开返回两1个线性无关的解。
通过将‘ExpansionPoint’设置为
I
n
f
Inf
Inf,找到围绕扩展点
∞
\infty
∞的其他级数解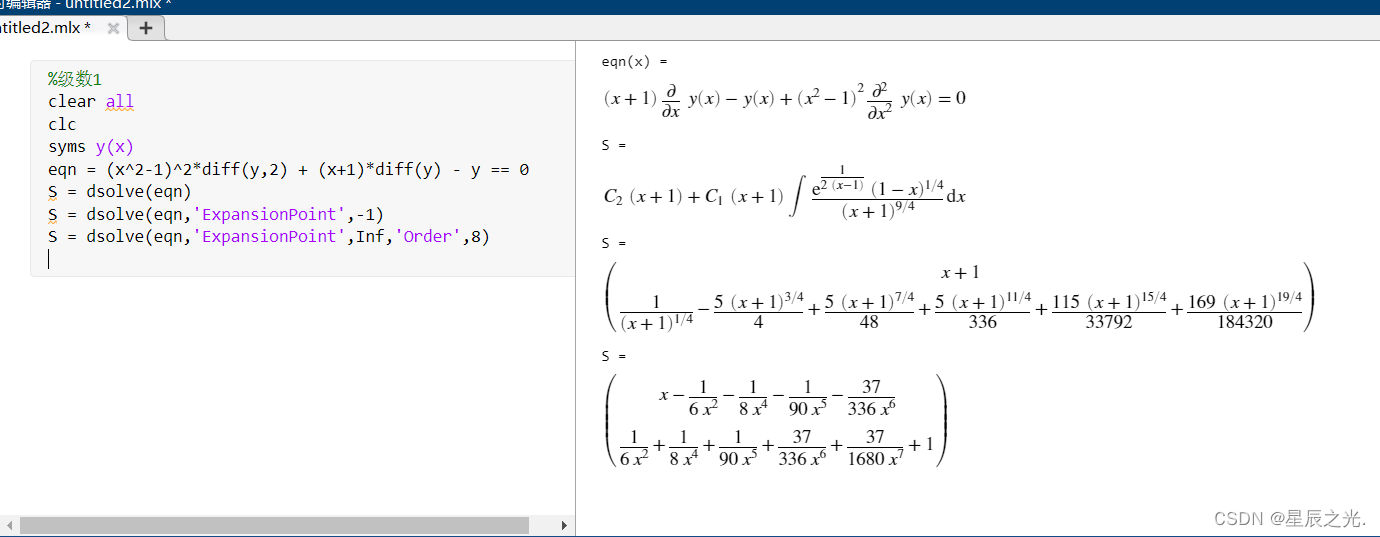 
设初始条件
y
(
0
)
=
2
y(0)=2
y(0)=2,则须添加下列代码：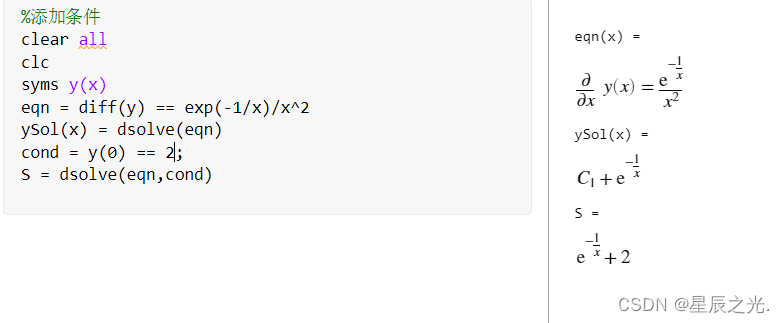
2
x
2
d
2
y
d
x
2
+
3
x
d
y
d
x
−
y
=
0
2{x^2}\frac{{{d^2}y}}{{d{x^2}}} + 3x\frac{{dy}}{{dx}} - y = 0
2x2dx2d2y+3xdxdy−y=0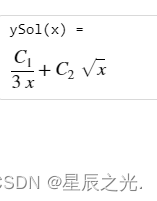 
The Airy equation.
d
2
y
d
x
2
=
x
y
(
x
)
\frac{{{d^2}y}}{{d{x^2}}} = x\operatorname{y} \left( x \right)
dx2d2y=xy(x) 
【本文地址】
今日新闻 |
推荐新闻 |