数学家们规定，多个同维向量相加，将得到一个新的向量

假设现有两个向量： \vec{AB},\vec{CD} ，若求 \vec{AB}+\vec{CD} ，则有：

三角形法则：首尾相连，将任意一个向量的起点，平移到另一个向量的终点处

下图所示，左边： \vec{AB}+\vec{CD}=\vec{AD} ，右边： \vec{CD}+\vec{AB}=\vec{CB}

且： \vec{AD}=\vec{CB} ，指两个向量方向相同、长度相同

平行四边形法则：起点相连，将两个向量的起点平移到一起，做出平行四边形

则有： \vec{AB}+\vec{AC}=\vec{AD}

这里以二维向量，即在平面直角坐标系中为例

假设： \vec{AB}=(1,2),\vec{AC}=(3,2)

则 \vec{AB}+\vec{AC}=(1+3,2+2)=\vec{AD}(4,4) ，见下图所示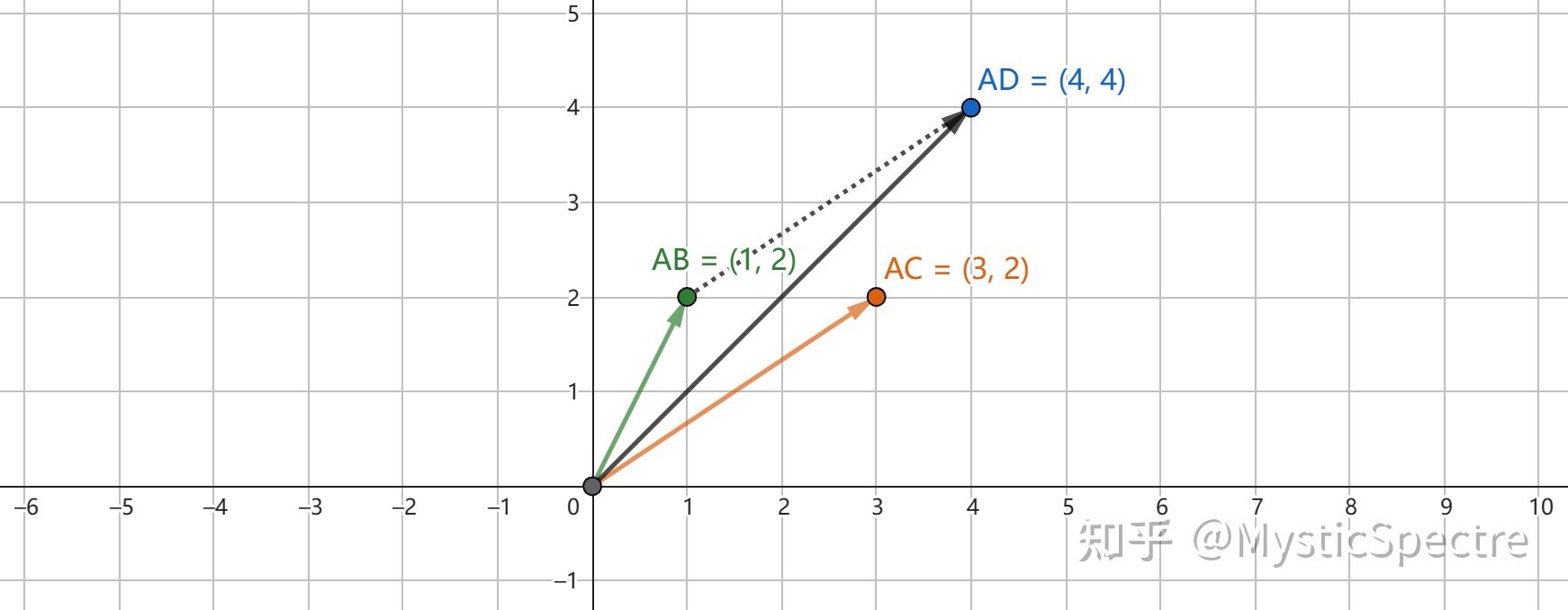

本质上，依然符合三角形法则，为了简化，我们将其定义为：

若存在两个同维向量相加，第1个向量 (a_{1},a_{2},a_{3},...a_{n}) ,第2个向量 (b_{1},b_{2},b_{3},...b_{n})

则两者相加后的向量为 (a_{1}+b_{1},a_{2}+b_{2},a_{3}+b_{3},...a_{n}+b_{n})

若存在多个同维向量相加，同理

基本定义： \vec{AB}-\vec{CD}=\vec{AB}+(-\vec{CD})

几何视角下：平移后起点相连，终点相连即做减后的向量

下图左边假设： \vec{AC}-\vec{AB} ，因为 \vec{AB}+\vec{BC}=\vec{AC} ，所以 \vec{AC}-\vec{AB}=\vec{BC}

下图右边假设： \vec{AB}-\vec{AC} ，因为 \vec{AC}+\vec{CB}=\vec{AB} ，所以 \vec{AB}-\vec{AC}=\vec{CB}

坐标视角下：坐标相减，对应维度的分量做差

设有： \vec{AB}=(6,6),\vec{CD}=(1,3)

则： \vec{AB}-\vec{CD}=(6-1,6-3)=(5,3)

设有： \vec{AB}=(6,6),\vec{CD}=(1,3),\vec{EF}=(-2,0)

则： \vec{AB}-\vec{CD}-\vec{EF}=(6-1+2,6-3-0)=(7,3)

数学家们规定，一个常数λ∈R，λ·\vec{a}=\vec{b}

例：λ=0， \vec{a}=(2,3) ， λ·\vec{a}=(0*2,0*3)=(0,0)

例：λ=-3， \vec{a}=(2,3) ，λ·\vec{a}=(-3*2,-3*3)=(-6,-9)

几何意义是指：向量a×λ后，该向量的方向不变，长度为原来的λ倍

例：λ=3， \vec{a}=(1,1) , λ·\vec{a}=(3*1,3*1)=(3,3)，如下图所示

我们知道，除以一个数非零常数a等价于乘以 \frac{1}{a} ，所以：

例：λ=2， \vec{a}=(2,3) ， λ÷\vec{a}=\frac{1}{λ}×\vec{a}=(2*\frac{1}{2},3*\frac{1}{2})=(1,\frac{3}{2})

加法交换律： \vec{a}+\vec{b}=\vec{b}+\vec{a}

加法结合律： (\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})

数乘交换律： λ\times\vec{a}=\vec{a}\timesλ ，λ∈R

数乘分配律1： λ\times(\vec{a}+\vec{b})=λ\times\vec{a}+λ\times\vec{b} ，λ∈R

数乘分配律2： (λ+ k)\times\vec{a}=λ\times\vec{a}+ k\times\vec{a} ，λ,k∈R

数乘结合律3： (λ\times k)\times\vec{a}=(λ\times \vec{a})\times k ，λ,k∈R

特别的： 1\times\vec{a}=\vec{a} ， -1\times\vec{a}=-\vec{a}

下面两个不适用于向量运算性质：特别要注意！

乘法结合律： (\vec{a}\times\vec{b})\times\vec{c}\ne\vec{a}\times(\vec{b}\times\vec {c}) ，含3个及以上向量相乘

等式不可约：若 \vec{a}\times\vec{b}=\vec{a}\times\vec{c} ，此时两边不可约掉 \vec{a}

一般我们用坐标，或数组来表示多个向量之间的加减，和与向量的数乘

下图为：向量相加( \vec{a}+\vec{b} )，适用于多个同维向量之间的相加或相减

下图为：向量的数乘(λ× \vec{a} )，适用于多个常数×一个向量