数学建模之微分方程模型总结

您所在的位置：网站首页 › logistic模型怎么用代码拟合出增长率和人口容量 › 数学建模之微分方程模型总结

数学建模之微分方程模型总结

2023-07-11 22:08| 来源: 网络整理| 查看: 265

一、基本概念

1.微分方程:包含连续变化的自变量，未知函数及其变化率（函数的微分或导数）的方程式。

2.使用场合：

1) 研究对象涉及某个过程。

2) 物体随着时间连续变化的规律。

3.例子:人口预测、发射火箭的高度

二、人口增长模型

（一）人口指数增长模型

现已知某个地区当年的人口数量为 $x_{0}$ ,初始时间 $t=0$ ，该地区人口数量随时间变化的函数为 $x\left ( t \right )$ ，人口增长率为r(r为常数)，则得到 $x\left ( t \right )$ 满足的微分方程:

$\frac{dx}{dt}=rx ,x(0)=x_{0}$

其中 $\frac{dx}{dt}$ 表示人口增长随时间的微分，即变化率， $rx$ 表示单位时间内 $x(t)$ 的增量，所以该模型的意义为在初值条件为 $x_{0}$ 的条件下人口增长随时间的变化率等于单位时间内人口增量。

由上式可以解出 $x(t)=x_{0}e^{rt}$ ,其中，当r>0时，人口将按指数规律无限增长。

模型缺点:只单纯考虑了人口的增长率，没有考虑自然环境，资源等对人口的影响，这是一种理想的情况，其最终得出的结论是人口将一直无限制增长下去。这显然是与现实情况相悖。

（二）改进的人口增长模型---logistic模型

资源和环境对人口的增长起到了抑制作用，且人口数量越多，这种抑制作用越强，具体表现在对增长率r的抑制上。这样一来，r随着x的增加而下降。

现将r表示成x的函数，即r(x)，同时令r(x)=ax+b,为了使a，b有意义，引入一些参数：

1）内禀增长率 r (内禀增长率指在给定的物理和生物的条件下，具有稳定的年龄组配的种群的最大瞬时增长率) :r是理论上x=0时的增长率，即r(0）=r,因此b=r。

2）人口容量 $x_{m}$ （在特定时空条件下，资源、生态、环境在保障人类基本生理需求的前提下，所能够供养的最大人口数）: $x_{m}$ 在生物学上称为环境容纳量，即当x= $x_{m}$ 时，人口不再增长，用函数关系式可以表示为 $r(x_{m})=ax_{m}+r=0$ ,从而解得 $a=-\frac{r}{x_{m}}$ 。

由已知，r(x)=ax+b，且b=r， $a=-\frac{r}{x_{m}}$ ，因此将三式联立整理可得:

$r(x)=-\frac{r}{x_{m}}x+r=(-\frac{x}{x_{m}}+1)r=r(1-\frac{x}{x_{m}})$

由 $\frac{dx}{dt}=rx ,x(0)=x_{0}$ ，加上 $r(x)=-\frac{r}{x_{m}}x+r=(-\frac{x}{x_{m}}+1)r=r(1-\frac{x}{x_{m}})$ ，用r(x)替换r，可得:

$\frac{dx}{dt}=rx(1-\frac{x}{x_{m}}),x(0)=x_{0}$

其中，rx表示人口自身的一个增长趋势，因子 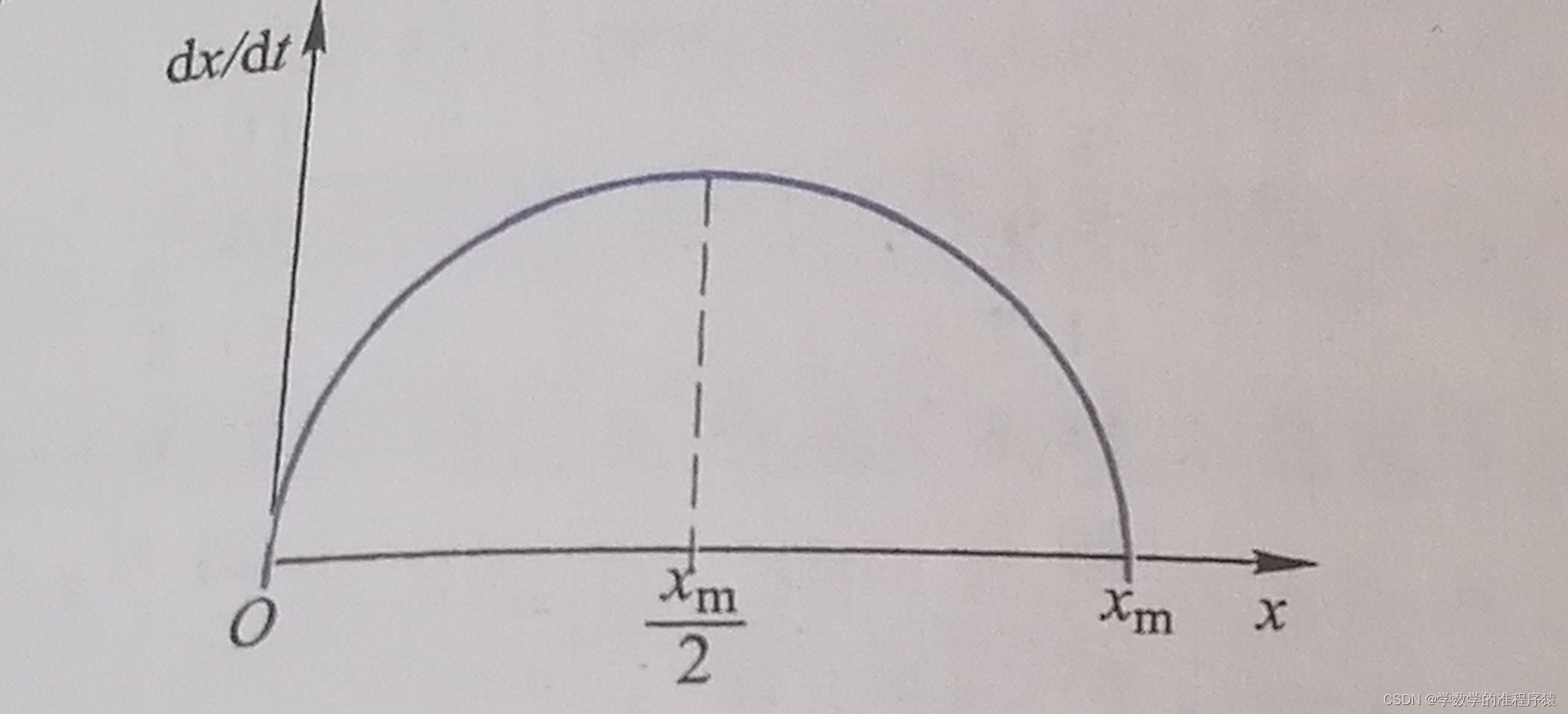$(1-\frac{x}{x_{m}})$ 则体现了资源和环境对人口增长的抑制作用，当x越大，rx越大， $(1-\frac{x}{x_{m}})$ 越小，人口增长是这两个因子共同作用的结果。对改进后的人口增长模型进行求解，可得

$x(t)=\frac{x_{m}}{1+\left (\frac{x_{m}}{x_{0}} -1\right )e^{-rt}}$

以x轴为横轴， $\frac{dx}{dt}$ 为纵轴做 $\frac{dx}{dt}=rx(1-\frac{x}{x_{m}}),x(0)=x_{0}$ 的图像，可得图1：

图1 x---dx/dt曲线

从图中可以看出，当 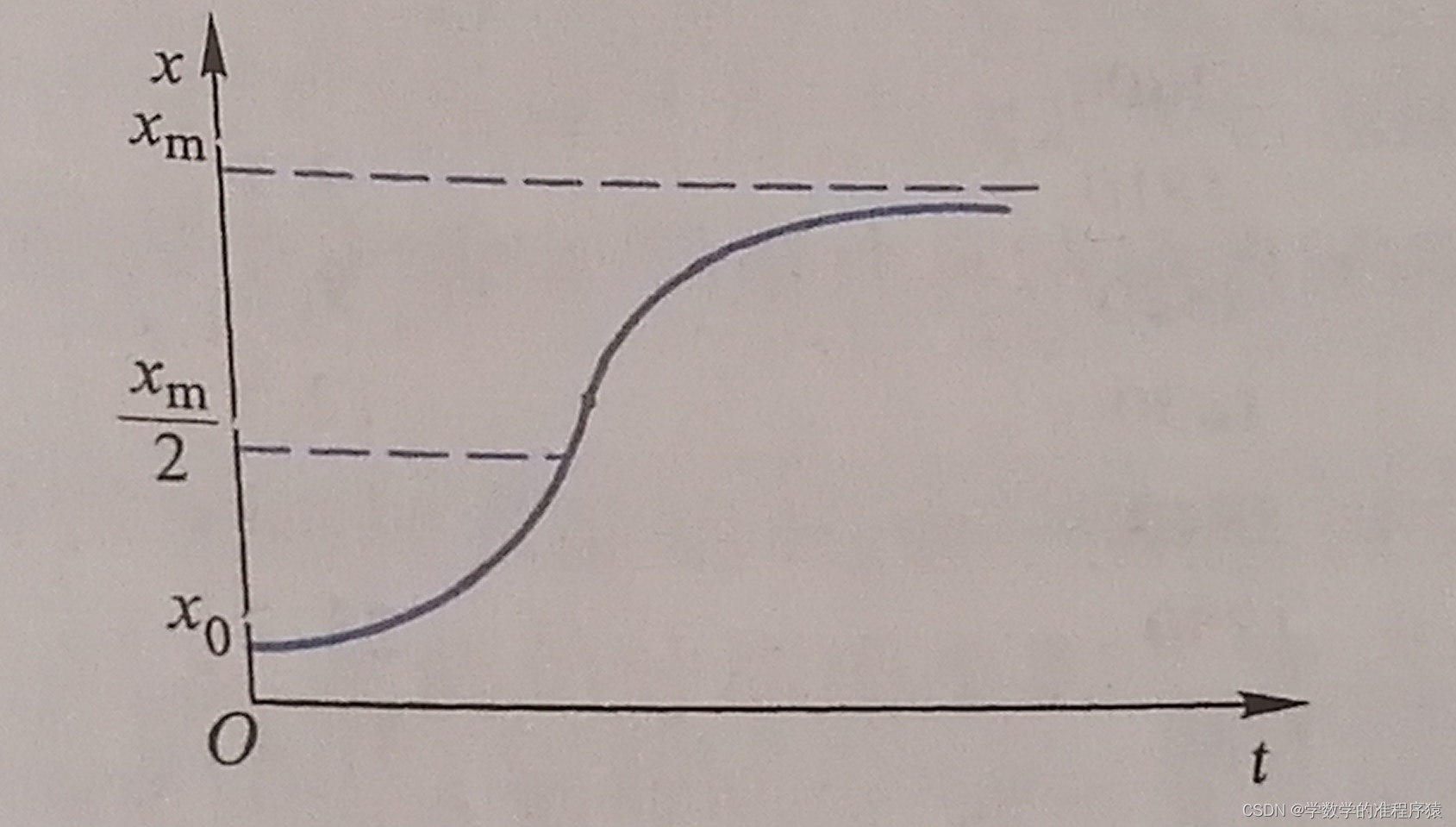$x=\frac{x_{m}}{2}$ 时， $\frac{dx}{dt}$ 最大，设t=0时， $x_{0}\frac{x_{m}}{2}$ ,随着t的增加 $\frac{dx}{dt}$ 增大，x增长越来越快，曲线x(t)呈下凸状上升； $x_{0}\frac{x_{m}}{2}$ 后 $\frac{dx}{dt}$ 变小，x此时增长越来越慢，因此，可得 $\lim_{x\rightarrow x_{m}}\frac{dx}{dt}=0$ ，根据上述分析可画出x(t)图像（见图2），可看出其是一条"S"形曲线。

图2 t--x曲线三、药物中毒急救模型-----房室模型

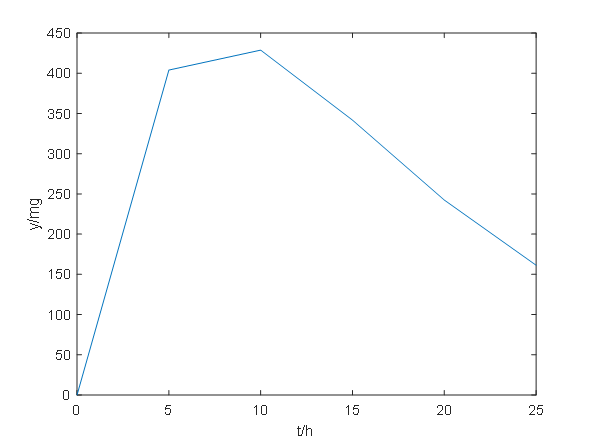
(一) 问题背景

人体服用一定药物后，血药浓度与人体血液总量有关，一般来说，血液总量约为人体体重的7%--8%，即体重为50--60kg的成年人血液总量大约为为4000ml，因此，血液系统中的血药浓度与药量之间可以相互转换。药物口服后迅速进入胃肠道，再由胃肠道外壁进入血液循环系统，被血液吸收，胃肠道中药物的转移率，即血液的吸收率，一般与胃肠道中的药量成正比，药物在被血液吸收的同时又通过代谢作用由肾脏排出体外，排出率一般与血液中药量成正比，假设血液系统中的血药浓度是均匀的，将血液系统看成一个房室。

(二) 问题描述

一天晚上，有两位家长带着孩子来到医院，你从两位家长口中得知孩子误食了11片治疗哮喘病的氨茶碱片，一般情况下，如果服用过量的氨茶碱片，会有致命的危险。现已知血药浓度>100微克/毫升会出现严重中毒，达到200微克/毫升时会致命。同时通过半衰期来确定血液系统对药物的吸收率与排出率（已知氨茶碱吸收的半衰期为5h,排出的半衰期为6h）。现建立数学模型，判断孩子的血药浓度是否已经达到危险水平。

(三) 模型假设

（1）假设孩子的血液总量为2000ml。

(2) 假设胃肠道中药物向血液系统的转移率与药量x(t)成正比，比例系数为λ(λ>0)，总剂量1100mg的药物在t=0瞬间进入胃肠道。

(3) 假设血液系统中药物的排出率与药量y(t)成正比，比例系数记为μ(μ>0)，t=0时血液中无药物。

（四）模型建立与求解

根据假设(2)，可建立胃肠道中血液系统药量x(t)的微分方程，式子如下:

$\frac{dx}{dt}=-\lambda x,x(0)=1100$

该式子的含义是单位时间内血液系统药量随时间的变化率等于单位时间内药量的减少量。

对上式进行求解可得

$x(t)=1100e^{-\lambda t}$

根据假设(3)，y(0)=0,药物从胃肠道向血液系统的转移等于血液系统对药物的吸收，y(t)由于吸收作用而增长的速度是λx，由于排出而减少的速度与y(t)本身成正比（μ>0），因此，建立微分方程:

$\frac{dy}{dt}=\lambda x-\mu y,y(0)=0$

该式子的含义是单位时间内血液系统中药量随时间的变化率等于单位时间内血液系统药量的增加量与单位时间内血液系统药量的排出量的差值。

对上式dy与dt的变化关系式求解可得

$y(t)=\frac{1100\lambda }{\lambda -\mu }(e^{-\mu t}-e^{-\lambda t})$

为了根据药物排出的半衰期为6h来确定μ，考虑血液中只对药物进行排出的情况，此时y(t)满足

$\frac{dy}{dt}=-\mu y$

若设在某时刻τ有y(τ)=a,则

$y(t)=ae^{-\mu (t-\tau )},t\geqslant \tau$

又

$y(\tau +6)=\frac{a}{2}$

得

$\mu =\frac{ln2}{6}=0.1155$

将λ=0.1386和μ=0.1155代入 $x(t)=1100e^{-\lambda t}$ 与 $y(t)=\frac{1100\lambda }{\lambda -\mu }(e^{-\mu t}-e^{-\lambda t})$ 得

$x(t)=1100e^{-0.1386t}$

$y(t)=6600(e^{-0.1155t}-e^{-0.1386t})$

表明血液系统中的药量y(t)随时间先增后减最终趋于0。

利用matalb软件对 $x(t)=1100e^{-0.1386t}$ 与 $y(t)=6600(e^{-0.1155t}-e^{-0.1386t})$ 进行作图，可得图3:

图3 胃肠道中药量x(t)与血液系统中药量y(t)

根据假设1，孩子的血液总量为2000ml，出现严重中毒的血药浓度为100微克/ml，出现致命的血药浓度为200微克/ml。分别相当于血液中药量y达到200mg和400mg。根据图三，药量y在约2h达到200mg，即孩子达到医院时已经出现严重中毒，如果不及时施救，药物将在5h后达到400mg。

四.传染病模型

(一) 问题背景:SARS病毒、新冠病毒的传播

(二) 问题描述：假设一个区域内爆发了传染病，这种传染病会造成一定的死亡率，现建立模型判断该传染病的传播趋势。

(三) S-I模型

1.模型假设

（1）假设该地区人群被分为两类: 健康人和患者。

（2）假设健康人和患者在人群中所占比例分别为s(t)和i(t)。

(3) 假设该地区绝对封闭，不考虑迁入和迁出人口。即总人口N不变。

(4) 假设每个患者每天接触的有效人数是常数λ，即接触率，有效接触即为患者与健康人接触后健康人立刻被感染。

2.模型建立与求解

根据上述模型假设，可建立方程

$Ni(t+\Delta t)-Ni(t)=N\lambda s(t)i(t)\Delta t$

该方程表明了人口总数乘以患者在 $\Delta t$ 时间内的变化量等于 $\Delta t$ 时间内新增的患者人数，建立患病人数随时间的差分，两边同时消去N有

$\frac{i(t+\Delta t)-i(t)}{\Delta t}=\lambda s(t)i(t)$

对 $\Delta t$ 取其趋于0时的极限，可得微分方程

$\frac{di}{dt}=\lambda s(t)i(t)$

又

$i(t)+s(t)=1$

因此，对 $\frac{di}{dt}=\lambda s(t)i(t)$ 改写，有

$\frac{di(t)}{dt}=\lambda (1-i(t))i(t), t0, i(0)=i_{0}$

解得

$i(t)=\frac{1}{1+(\frac{1}{i_{0}}-1)e^{-\lambda t}}$

根据微分方程和结果可得传染病曲线和预测曲线（见图4,5）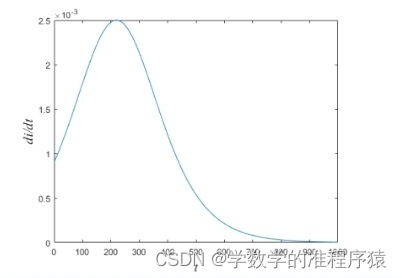

图4 传染病曲线

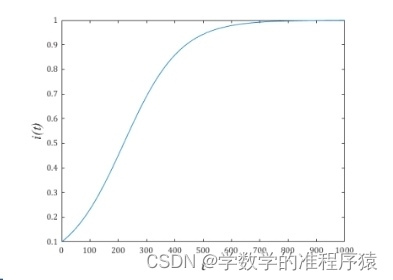图5 预测曲线

从图中可以得出以下结论:

(1) 随着时间推移，病人的比例会接近于1。

(2) 当i(t)=0.5时，此时 $\frac{di}{dt}$ 最大，也即传染病高峰即将来临。

(3) $t_{m}=\frac{1}{\lambda }ln(\frac{1}{i_{0}}-1)$ ,此时 $k_{i(t)-tmax}$ 。

3.模型缺点

(1)模型最终结论是病人比例趋近于1，与实际不符。

(2)模型只考虑了健康者被感染，没有考虑感染者被治愈，不合理。

(四)S-I-S模型

1.模型假设

（1）每天被治愈的人的比例为μ。

(2) 病人被治愈后仍有二次感染的可能。

2.模型建立与求解

根据条件建立差分方程

$Ni(t+\Delta t)-Ni(t)=N\Delta t[\lambda i(t)(1-i(t))-\mu i(t)]$

令 $\Delta t$ 趋于0，建立微分方程

$\frac{di(t)}{dt}= \lambda i(t)(1-i(t))-\mu i(t), t0, i(0)=i_{0}$

解得

$i(t)=\left\{\begin{matrix} \frac{1}{\frac{\lambda }{\lambda -\mu }+(\frac{1}{i_{0}}-\frac{\lambda }{\lambda -\mu })e^{\frac{1}{(\lambda -\mu )t}}} ,\lambda \neq \mu & & \\ \frac{1}{\lambda t+\frac{1}{i_{0}}} ,\lambda =\mu & & \end{matrix}\right.$

令 $\sigma =\frac{\lambda }{\mu }$ ，即日接触率与日治愈率的比值，对上式化简整理有

$\left\{\begin{matrix} & \frac{di}{dt}= -\lambda i[i-(\frac{1}{\sigma })] , t0\\ & i(0)=i_{0} \end{matrix}\right.$

$i(t)=\left\{\begin{matrix} \frac{1}{\frac{1}{1-\frac{1}{\sigma }}+(\frac{1}{i_{0}}-\frac{1}{1-\frac{1}{\sigma }})e^{-\lambda (1-\frac{1}{\sigma })t}} ,\sigma \neq 1& \\ & \frac{1}{\lambda t+\frac{1}{i_{0}}},\sigma =1 \end{matrix}\right.$

令t趋于无穷，有

$i(t)=\left\{\begin{matrix} & 1-\frac{1}{\sigma } ,\sigma 1\\ & 0,\sigma \leqslant 1 \end{matrix}\right.$

讨论 $\sigma =\frac{\lambda }{\mu }$ （定义其为传染强度）

(1) $\sigma$ 是一个阈值

(2)若 $\sigma$ $\leqslant1$ ，代表新增病人数小于治愈人数，即t趋于无穷时，所有病人都将被治愈。

(3)若 $\sigma 1$ ，代表新增病人数大于治愈人数，即t趋于无穷时，总有一定比例的人成为病人。

(五)S-I-R模型

1.模型假设

(1)设任意时间内，病人，健康者，治好者(治好者后不会再次感染）的比例为s(t),i(t),r(t),且s(t)+i(t)+r(t)=1.

(2)病人日接触率为λ，治愈率为μ.

(3)人口总数为N，一定程度下保持不变

2.模型建立

$\left\{\begin{matrix} s(t) +i(t)+r(t)=1& & \\ N\frac{dr}{dt}=\mu Ni(t)& & \\ N\frac{di}{dt}=\lambda Ns(t)i(t)-\mu Ni(t)& & \\ N\frac{ds}{dt}=-\lambda Ns(t) i(t)& & \\ i(0)=i_{0},s(0)=s_{0},r(0)=0& & \end{matrix}\right.$

3.模型求解

求解结果见图6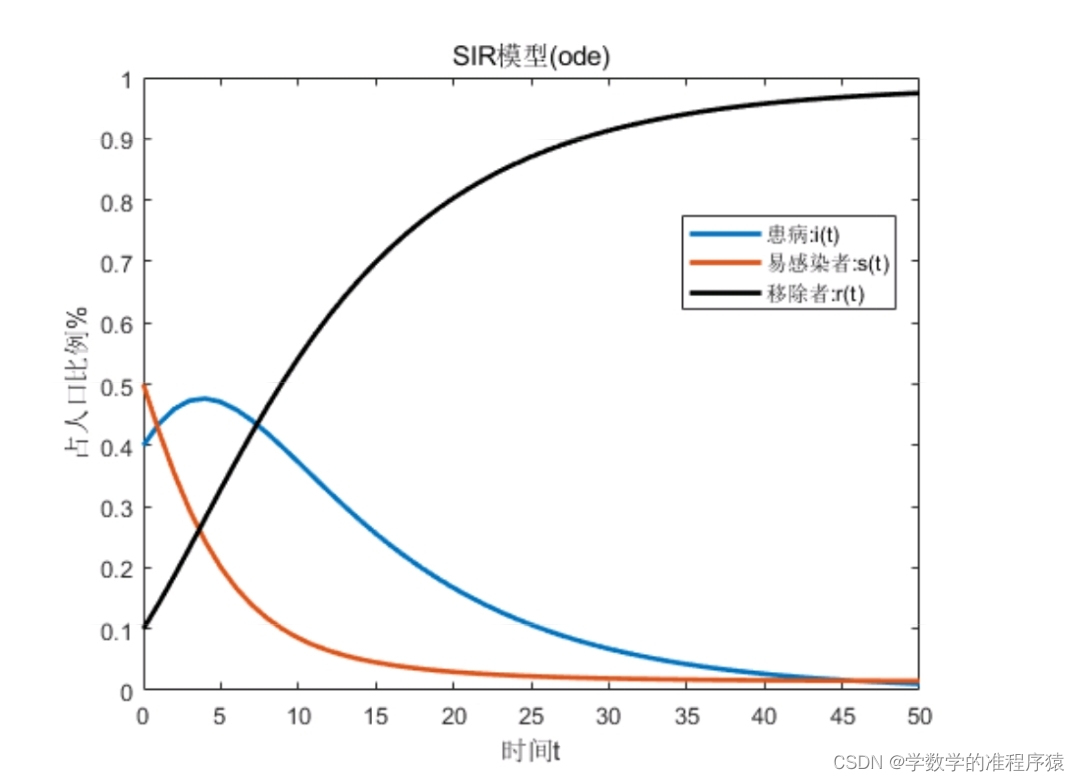

图6 方程组求解曲线图附录

附录1:求解方程组MATLAB代码:

clc,clear lam=0.4; mu=0.1; I=0.4; s=0.5; tspan=[0:1:50]; yo=[I S]; [t,y]=ode45(@(t,y)SIRfun(t,y,lam,mu),tspan,yo); r=1-y(:,1)-Y(:,2); plot(t,y(:,1),t,y(:,2),t,r,'k','Linewidth',2); legend('患病:i(t)','易感者:s(t)','移出者:r(t)','Location'); ylabel('占人口比例'); xlabel('t'); title('SIR模型(ode）'); function dydt=func(t,y,lam,mu) dydt=zeros(2,1); dydt(1)=lam*y(1)*y(2)-mu*y(1); dydt(2)=-lam*y(1)*y(2); end;

附录2:方程 $\frac{dx}{dt}=rx(1-\frac{x}{x_{m}}),x(0)=x_{0}$ 的求解过程

令 $x{}'=\frac{x}{x_{m}}$ ，则 $x=x'x_{m}$ ,因此上式可改写为