机器学习入门专栏其他几个章节:

机器学习入门（一）线性回归

机器学习入门（二）KNN

机器学习入门（三）朴素贝叶斯

机器学习入门（四）决策树

机器学习入门（五）集成学习

机器学习入门（六）支持向量机

机器学习入门（八）主成分分析

机器学习入门（九）无监督学习

在机器学习入门（六）中，已经通过pipeline快速实现了多项式回归。代码如下：

这个方式省略了很多步骤，并且也无法得知PolynomialFeatures是如何运作的。

现在有（a，b）两个特征，使用degree=2的二次多项式则为（1，a, a^2, ab, b ,b^2)。 PolynomialFeatures主要有以下几个参数：

degree：度数，决定多项式的次数

interaction_only： 默认为False，字面意思就是只能交叉相乘，不能有a^2这种.

include_bias: 默认为True, 这个bias指的是多项式会自动包含1，设为False就没这个1了.

order：有"C" 和"F" 两个选项。官方写的是在密集情况（dense case）下的输出array的顺序，F可以加快操作但可能使得subsequent estimators变慢。 利用代码试验一下：

得到结果如下: 如果是c=[[a],[b]]这种形式，生成的多项式就没有ab交叉项了，只有[[1,a,a^2], [1,b,b^2]] 。

多项式回归是多元线性回归的一个特例 所以其本质是一个求解多元线性方程组的问题： f ( x ) = w T x + b f(x) = w^Tx+b f(x)=wTx+b 或者: f ( x ) = w n x n + w n − 1 x n − 1 + . . . + w 2 x 2 + w 1 x + b f(x)=w_nx^n+w_{n-1}x^{n-1}+...+w_2x^2+w_1x+b f(x)=wn​xn+wn−1​xn−1+...+w2​x2+w1​x+b 这里无论是 x n x^n xn还是 x n x_n xn​，其实本质都一样.

把b处理一下写成 w 0 , x 0 w_0,x^0 w0​,x0的形式带入，以矩阵的形式更容易理解： [ 1 x 0 x 0 2 ⋯ x 0 n − 1 x 0 n 1 x 1 x 1 2 ⋯ x 1 n − 1 x 1 n ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ 1 x n x n 2 ⋯ x n n − 1 x n n ] [ w 0 w 1 ⋮ w n ] = [ y 0 y 1 ⋮ y n ] \left[\begin{array}{c}1&x_0&x_0^2&\cdots &x_0 ^{n-1}& x_0^n\\ 1&x_1&x_1^2&\cdots &x_1^{n-1}&x_1^n\\ \vdots &\vdots&\vdots&\ddots&\vdots&\vdots\\ 1&x_n&x_n^2&\cdots &x_n^{n-1}&x_n^n\end{array}\right]\begin{bmatrix}w_0\\w_1\\\vdots \\w_n\end{bmatrix}= \begin{bmatrix} y_0\\y_1\\ \vdots\\ y_n\end{bmatrix} ⎣ ⎡​11⋮1​x0​x1​⋮xn​​x02​x12​⋮xn2​​⋯⋯⋱⋯​x0n−1​x1n−1​⋮xnn−1​​x0n​x1n​⋮xnn​​⎦ ⎤​⎣ ⎡​w0​w1​⋮wn​​⎦ ⎤​=⎣ ⎡​y0​y1​⋮yn​​⎦ ⎤​ 左边是关于x的矩阵，右边是关于w系数的矩阵，每一个系数w都对应x中的一列。而PolynomialFeatures就是用来生成关于x的矩阵的。

然后再用LinearRegression学习，获得相应的w。

说的再简单一点，比如现在有横坐标[[a], [b], [c]], 纵坐标[[x], [y], [z]]，通过PolynomialFeatures(degree=2）即生成二次多项式矩阵，degree是多少，就是几次。 [ 1 a a 2 1 b b 2 1 c c 2 ] × w = [ x y z ] \begin{bmatrix} 1 & a&a^2\\ 1&b&b^2\\ 1&c&c^2\end{bmatrix}\times w= \begin{bmatrix} x\\ y\\ z \end{bmatrix} ⎣ ⎡​111​abc​a2b2c2​⎦ ⎤​×w=⎣ ⎡​xyz​⎦ ⎤​ 其中每一列都会对应生成一个系数，很直观的理解，如果是一维的，LinearRegression就会学得一次项系数，二维的就会学得二次项系数，一次类推。所以最后LinearRegression模型中的coef_参数返回的是一个关于系数的list。

首先创建数据并且添加噪音:

生成这样的数据：

然后实现多项式矩阵,并且训练模型,查看训练出来的系数w和截距b:

结果如下： 正好三个系数，分别对应常数项，一次项，二次项。 然后绘制图像：

生成图像，由于二次项系数为负，所以这个二次函数先增后减。：

其实，想要获得w系数，更直接的方式是利用正规方程： w = ( X T X ) − 1 X T y w=(X^TX)^{-1}X^Ty w=(XTX)−1XTy

想要得到这个公式也非常简单, 已知我们要求解 X w = y Xw=y Xw=y，两边同时乘上 X T X^T XT得： X T X w = X T y X^TXw=X^Ty XTXw=XTy

将左边的 X T X X^TX XTX除到右边即可

python代码验证：

这里X是经过PolynomialFeatures处理之后的矩阵，对应之前代码中的XX2。

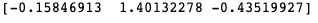np.linalg.inv()表示逆矩阵，X.T就是转置，@等价于.dot()操作，可以获得结果如下： 和之前求的w和b一模一样，说明结果完全正确！